



Recursos Naturales y Ambiente
Erosividad mensual de la lluvia determinada a partir de información de cuatro estaciones meteorológicas de Nicaragua
Monthly rainfall erosivity determined from information of four meteorological stations from Nicaragua
La Calera
Universidad Nacional Agraria, Nicaragua
ISSN: 1998-7846
ISSN-e: 1998-8850
Periodicidad: Semestral
vol. 22, núm. 39, 2022
Recepción: 08 Julio 2022
Aprobación: 01 Diciembre 2022

Resumen: La estimación de la erosión del suelo con el método de la ecuación universal revisada de pérdida de suelo (RUSLE) requiere estimar el índice de erosividad de la lluvia. El objetivo del estudio fue determinar el índice de erosividad mensual de la lluvia Rmes utilizando los registros de las estaciones meteorológicas Aeropuerto de Managua y Rivas (Zona del pacífico), Jinotega (zona central Norte) y Juigalpa (zona central sur). Se utilizaron los pluviogramas de las estaciones para calcular el índice de erosividad de la lluvia con la expresión propuesta por Wischmeier y Smith en 1978. Al pluviograma de cada tormenta se le estimó la energía cinética total de la tormenta (E) y la intensidad máxima en 30 minutos (I30), se obtuvo el índice de erosividad de la tormenta Rt como el producto EI30, y se obtuvo el índice de erosividad mensual Rmes como la suma de todos los Rt de las tormentas de un mes. Se utilizaron los datos mensuales de precipitación para calcular el índice modificado de Fournier (IMF). Se obtuvieron ecuaciones lineales de correlación de los valores mensuales del índice de erosividad de la lluvia y el índice modificado de Fournier con un coeficiente de determinación mayor que 0.70. Se evaluó la bondad del ajuste de las ecuaciones de correlación mediante los parámetros coeficiente de determinación (r2), porcentaje de sesgo PBIAS y raíz del error cuadrático medio (RMSE), resultando que las ecuaciones de correlación determinadas son buenas para estimar el índice de erosividad de la lluvia a escala mensual. Las ecuaciones podrían ser utilizadas en los meses de mayo a octubre, cuando se presentan las lluvias significativas en los departamentos de Managua, Rivas, Jinotega y Chontales. Los máximos valores del índice de erosividad de la lluvia R se presentaron en los períodos de mayo-junio y septiembre-octubre.
Palabras clave: erosión hídrica, pluviograma, tormenta, índice modificado de Fournier.
Abstract: The estimation of soil erosion with the Revised Universal Soil Loss Equation (RUSLE) method, requires estimating the rainfall erosivity index. The aim of this study is to determine the monthly rainfall erosivity index for the meteorological stations Managua Airport, Rivas at pacific south part, Jinotega at central north part and Juigalpa at central south part of the country. Pluviographs from the stations were used to calculate the rainfall erosivity index, using the equations proposed by Wischmeier & Smith in 1978.The total kinetic energy (E) was estimated for each storm and its maximum intensity in 30 minutes of duration (I30), the storm erosivity index Rt was estimated as the product of EI30, and the monthly rainfall erosivity index Rmes was estimated as the sum of all the Rt from the storms that belong to a month. The monthlies precipitations data were used to calculate the Fournier modified index IMF. It was obtained linear correlation equations from the monthly values of rainfall erosivity index, and the Fournier modified index with a coefficient of determination greater than 0.70. It was verified the performance of the correlation equations with the coefficient of determination (r2), the Percent Biass (PBIAS) and the root mean square error (RMSE), resulting those the determined correlation equations are good to estimate rainfall erosivity index at monthly scale. The equations could be used through the months May to October, when are presents the significant rainfalls in the Managua, Jinotega, Juigalpa and Rivas departments. The maximums values of the erosivity index R were presents in the periods May-June and September-October.
Keywords: Hydric erosion, pluviograph, storm, Fournier modified index.
En Nicaragua, la mayor actividad económica es la agropecuaria y tiene influencia en las tasas de erosión anual de los suelos y en el rendimiento de los cultivos. La agricultura y ganadería practicada en suelos con vocación forestal incrementan la tasa de erosión, por lo que se requiere estudios que permitan determinar los niveles de erosión actual para hacer los cambios en el uso del suelo, según su vocación, y así disminuir la pérdida del suelo. Uno de los métodos utilizados para hacer la estimación de la pérdida de suelo es la fórmula universal revisada de pérdida de suelo (RUSLE, por sus siglas en idioma inglés), la cual emplea el índice de erosividad de la lluvia R, que según Wischmeier y Smith (1978), se estima en función de la energía total de la tormenta E y la intensidad máxima de la lluvia en un período de 30 minutos. Estos dos solamente se pueden estimar en estaciones que registran de forma continua la precipitación y con intervalos cortos de tiempo. En Nicaragua hay muy pocas estaciones de este tipo, la mayoría de las estaciones registran datos a nivel diario, y en ellas se dispone de registros mensuales de precipitación, por lo que se requiere desarrollar un método que permitan estimar el valor del índice de erosividad mensual de la tormenta Rmesa partir de datos de precipitaciones mensuales.
Arnoldus (1977) en un estudio en Marruecos utilizó datos mensuales de precipitación para obtener buenas correlaciones del índice de erosividad anual Ra y el índice modificado de Fournier (IMF), recomendando este procedimiento en la estimación de Ra para sitios con escasos datos de intensidades de lluvias. Los autores Renard y Freimund (1994) utilizaron datos de precipitación mensual para estimar el IMF y el índice de erosividad anual Ra, con un alto coeficiente de correlación. En Argentina, Ares et al. (2012) estudiaron la correlación de los valores estacionales Rest y la precipitación, obteniendo buenos resultados (r2 = 0.83) concluyendo que las estimaciones de Rest a nivel estacional a partir de datos de precipitación son aceptables. En este estudio se plantea la correlación del índice de erosividad mensual Rmes y el IMF mensual en función de las precipitaciones mensuales; esto permitiría estimar el índice de erosividad Rmes en las regiones del país que no cuenten con datos de precipitaciones pluviográficas.
MATERIALES Y MÉTODOS
Metodología
En este estudio se utilizó la metodología propuesta por Wischmeier y Smith (1978) y Renard et al. (1997), en la que se determinan los valores del índice de erosividad de la lluvia para cada tormenta Rt, en función de su energía cinética total y la intensidad máxima en 30 minutos. El índice de erosividad mensual de la lluvia Rmes se estima como la suma de todos los Rt que se presentaron en un mes. Con la información de Rmes obtenida, se presenta la variación mensual del índice de erosividad mensual media R en las estaciones pluviográficas Aeropuerto de Managua, Rivas, Jinotega y Juigalpa. Considerando la escasez de datos pluviográficos para la determinación del índice de erosividad de la lluvia, se relaciona el índice modificado de Fournier (IMF) con el índice de erosividad mensual Rmes, para obtener ecuaciones lineales de correlación que permitan estimar el índice Rmes a partir de datos de precipitación mensuales. Otros autores como Pérez y Senent (2015); Rivera y Gómez (1991); Blanco Chávez (2019) y Gutiérrez y Blanco Chávez (2021) han aplicado esta metodología. Se evaluó la bondad del ajuste de las ecuaciones de correlación lineal mediante los parámetros: coeficiente de determinación (r2), porcentaje de sesgo PBIAS y raíz del error cuadrático medio RMSE.
La información de precipitación se obtuvo de los registros del Instituto Nicaragüense de Estudios Territoriales (INETER), los datos obtenidos corresponden a precipitaciones de cada tormenta analizada (mm) e intensidad máxima en 30 minutos (mm h-1), derivados del pluviograma y precipitaciones mensuales (mm). Se analizaron las precipitaciones de las estaciones meteorológicas con registros pluviográficos que disponen de datos con intervalo de cinco minutos, como es el caso de las estaciones Aeropuerto de Managua (código 69027), Rivas (código 69070), Jinotega (código 55020) y Juigalpa (código 69034). Las dos primeras estaciones están en la región del Pacifico y las otras dos en la región central Norte y Sur del país respectivamente.
Para la estación Aeropuerto de Managua, en el período de registro 2000-2016 se dispuso de datos en 116 meses, con 466 eventos de precipitación. Para la estación Jinotega, en el período de registro 1996-2015 se dispuso de datos en 120 meses, con 383 eventos de precipitación. En la estación Juigalpa, período de registro 1972-1991, se dispuso de datos en 96 meses, con 375 eventos de precipitación. Para la estación Rivas, en el período de registro 1970-1991, se dispuso de datos de 136 meses, con 575 eventos de precipitación.
Las variables del estudio se calcularon según el procedimiento descrito a continuación.
Índice de erosividad de la lluvia (Rt)
El valor del índice de erosividad de la lluvia para una tormenta (Wischmeier y Smith, 1978), se calcula como el producto de la energía total de la tormenta (E) por la intensidad máxima de la tormenta en un período de 30 minutos (I30):
Rt = EI30 (1)
Donde:
Rt = Índice de erosividad de la lluvia (MJ ha-1 - mm h-1), para una tormenta.
E = Energía cinética total de la tormenta (MJ ha-1)
I30 = Intensidad máxima de la tormenta en 30 minutos (mm h-1)
Se analizaron las lluvias con una altura mayor o igual a 12.4 mm. La suma de los valores de EI30 de las tormentas de un período dado es una medida numérica del potencial erosivo de la lluvia en ese período.
La energía de la tormenta E es un indicador del volumen y la escorrentía de esa tormenta; la intensidad I30 indica la tasa de duración del pico de destrucción del suelo y escorrentía. El producto EI30, técnicamente, indica cómo la desagregación de las partículas del suelo es combinada con la capacidad de transporte.
El valor de la energía cinética total E de una tormenta se estima con:

Donde:
e: es la energía cinética unitaria en el tramo k de la lluvia (MJ / (ha-mm), h: es la altura de lluvia en el tramo “k” en mm, “m” es el número de tramos de la lluvia en estudio, y E se expresa en MJ ha-1.
La energía de la tormenta es función de la cantidad de lluvia y de todas las intensidades componentes de la tormenta. Brown y Foster (1987), como se citó en Renard et al. (1997) proponen estimar la energía cinética unitaria de la tormenta mediante la ecuación:
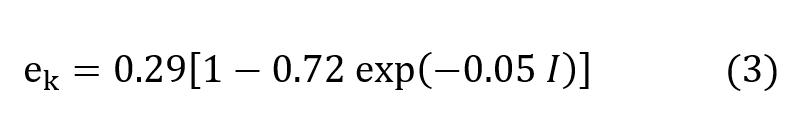
Donde:
ek: energía cinética unitaria de un tramo “k” de lluvia en Megajulio) por hectárea por milímetro de altura de lluvia del tramo analizado (MJ / (ha-mm)).
I: intensidad del tramo “k” de la tormenta (mm h-1).
Para utilizar las ecuaciones (2) y (3) la tormenta se divide en tramos, cada tramo “k” consiste en el intervalo de tiempo en el cual la intensidad de la lluvia es aproximadamente constante, esto es cuando el gráfico del pluviograma tiene pendiente casi uniforme.
Se determinaron los valores de R de las tormentas seleccionadas en las estaciones pluviográficas con las ecuaciones (1), (2) y (3) y el valor mensual como la suma de los valores de R de las tormentas de cada mes.
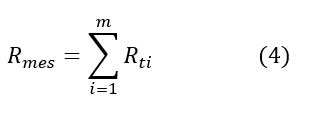
Donde:
m = Número de tormentas en un mes
Rmes = Índice de erosividad de la lluvia en el mes (MJ ha-1 - mm h-1) / mes
Rti= Índice de erosividad de la lluvia de la tormenta "i" (MJ ha-1 - mm h-1) en un mes
Índice Modificado de Fourier (IMF)
Arnoldus (1977) plantea que cuando no existe una adecuada densidad de estaciones pluviográficas, para estimar el índice R, se puede utilizar una aproximación correlacionando R y el índice modificado de Fournier. En ese estudio presenta el índice modificado de Fournier como:

Donde:
IMF = Índice modificado de Fournier (mm)
Pi = Lluvia promedio mensual del mes "i" (mm)
P = Lluvia promedio anual (mm)
Arnoldus (1977) también demuestra que existe una alta correlación entre el índice de erosividad Ra y el índice IMF. Los resultados concuerdan muy bien con los valores de aquellas estaciones para las cuales el índice Ra ha sido calculado con el método del RUSLE. Los resultados anteriores fueron confirmados por Renard y Freidmund (1994) en Estados Unidos de América (EE. UU.) con un alto coeficiente de correlación. El IMF ha sido utilizado en estudios para estimar Ra en varios países como Colombia (Rivera y Gómez, 1991), España (De Luis et al., 1997; Pérez y Senent, 2015) y Marruecos (Saldaña et al., 2014). Se determinaron los valores mensuales del IMF en las estaciones pluviográficas derivados de la ecuación (5), dividiendo el cuadrado de la precipitación del mes en cuestión (Pi2) por la precipitación promedio anual de la serie (P), de esa forma se obtiene un IMF para cada mes.
Análisis estadístico
Para determinar las relaciones entre el IMF y el R, se llevaron a cabo análisis de regresiones lineales simples. Así mismo, se evaluaron los coeficientes de determinación lineal r2, porcentaje de sesgo PBIAS y raíz del error cuadrático medio RMSE; este análisis se efectuó con datos mensuales. Los análisis estadísticos fueron realizados en la hoja de cálculo Excel.
Ecuaciones de correlación
Se procedió al análisis de correlación entre las variables R mensual e IMF mensual, adoptándose una correlación lineal como la de mejor ajuste. Se evaluó la bondad del ajuste obtenido. Los parámetros de evaluación utilizados fueron: coeficiente de determinación lineal r2 (6), porcentaje de sesgo PBIAS (7) y raíz del error cuadrático medio RMSE (8). El coeficiente r2 mide la asociación lineal entre dos variables, es adimensional y varía de cero a uno, mientras más se acerca a uno, hay mayor asociación entre las variables. El porcentaje de sesgo PBIAS evalúa la tendencia promedio entre el dato observado y el estimado, deberá ser ≤ ±25% y r2 ≥ 0.6 (Moriasi et al., 2007). El RMSE permite cuantificar la magnitud de la desviación de los valores estimados respecto a los observados, o sea, la exactitud. Las ecuaciones (6), (7) y (8) son las utilizadas para el cálculo de r2, PBIAS y RMSE.
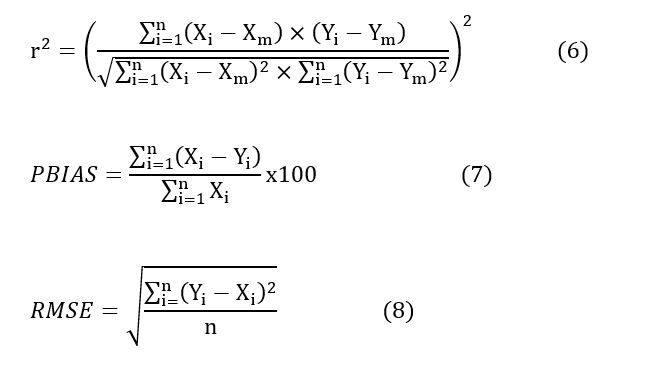
Dónde: Xi = valor observado, Xm = valor medio observado, Yi = valor estimado, Ym = valor medio estimado, n = número de pares de datos.
Debido a que el RMSE puede resultar con un valor muy grande, ya que depende de la escala de valores de las series de datos, es difícil determinar su magnitud sin un punto de referencia, por lo cual se introduce la variable error cuadrático medio normalizado (MEF) que normaliza el RMSE con respecto a la desviación estándar, y poder evaluar la eficiencia de la ecuación de correlación, mientras más bajo es MEF mejor es el desempeño del modelo, varía de 0 a α (Zhong y Dutta, 2015).
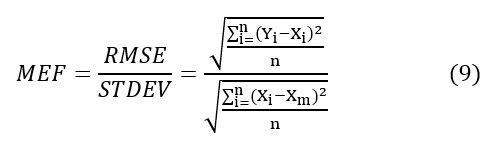
Dónde: MEF es el error cuadrático medio normalizado, RMSE es el error cuadrático medio y STDEV es la desviación estándar de los datos.
RESULTADOS Y DISCUSIÓN
Estación Aeropuerto de Managua
Utilizando las ecuaciones índice de erosividad de la lluvia (1), energía cinética total (2), y energía cinética unitaria de un tramo (3) se estimó Rt de cada tormenta para el período 2000-2016 y se obtuvieron los valores de erosividad de la lluvia de cada mes Rmescon la ecuación de índice de erosividad de la lluvia en el mes (4). En la estación Aeropuerto de Managua los valores mensuales Rmesse presentan principalmente en los meses de mayo a octubre. Los otros meses del año no tienen valores significativos de Rmes. Con la ecuación del índice modificado de Fournier (5) se calculó los valores de IMF mensuales. La Figura 1 (a y b) muestran las variaciones de R en IMF promedios mensuales, donde se puede observar que el índice IMF tiene una distribución bimodal dado que es función de las precipitaciones y que la erosividad R también sigue una distribución bimodal. Los máximos valores de R promedio mensual se presentan en los períodos más lluviosos del año, mayo-junio y septiembre-octubre; para el primer período el valor máximo se presentan en mayo con un valor de 1 014 MJ ha-1 - mmh-1, y para el segundo período el valor máximo se presenta con un valor de 1 323 MJ ha-1 - mm h-1.
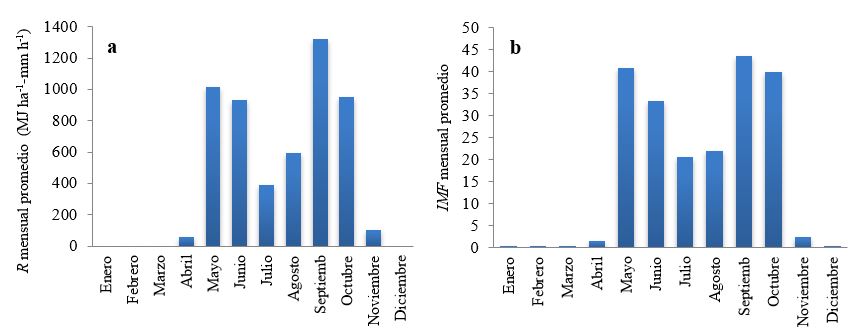
Se obtuvo la ecuación de correlación lineal para los datos del índice de erosividad de la lluvia Rmes e índice modificado de Fournier IMF mensual de la estación Aeropuerto de Managua, para el período 2000-2016. El coeficiente de determinación obtenido fue r2 = 0.75, indicando que hay una buena relación lineal entre las variables IMF mensual y R mensual. La ecuación de correlación obtenida es:
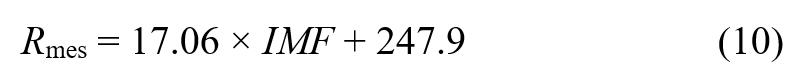
La ecuación de correlación (10) se utilizó para estimar los valores de R mensual del período de datos analizados, a estos los llamaremos "R estimado". A los valores R mensual calculados a partir de los datos pluviográficos y la ecuación (4), los llamaremos "R observado". Se procedió a correlacionar el valor R estimado con el valor R observado.
En el Cuadro 1 se indica la comparación de los datos estadísticos obtenidos de Rmesen la estación Aeropuerto de Managua. Se puede ver que la ecuación de correlación (10) sobreestima el valor mínimo de Rmes con una diferencia de 245 MJ ha-1 - mm h-1, sobrestima el valor máximo por 129.1 MJ ha-1 - mm h-1, y subestima el valor medio, con una diferencia de 11.9 MJ ha-1 - mm h-1. La desviación estándar de Rmes estimado indica que el dato estimado varía menos alrededor de la media que el dato observado, con una diferencia de 117.3. Haciendo el análisis de desempeño de la ecuación de correlación (10) a través de los parámetros coeficiente de determinación (r2) y porcentaje de sesgo (PBIAS), el resultado de la estimación indica que el dato estimado se considera bueno para r2 (0.75) y muy bueno para PBIAS (1.53 %), y bueno para MEF (0.50).
| Estadístico | R mensual observado | R mensual estimado | |
| Mínimo | 9.8 | 254.8 | |
| Máximo | 3 546.6 | 3 675.7 | |
| Medio | 779.7 | 767.8 | |
| Desviación estándar | 788.3 | 671.0 | |
| r2 | 0.75 | ||
| PBIAS (%) | 1.53 | ||
| RMSE | 390.60 | ||
| MEF = RMSE/DesvStand | 0.50 | ||
| Cantidad de datos | 116 |
r2: coeficiente de determinación lineal, PBIAS: porcentaje de sesgo, RMSE: raíz del error cuadrático medio, MEF: error cuadrático medio normalizado, DesvStand: desviación estándar.
Otros autores como Arnoldus (1977) en Marruecos, Renard y Freidmund (1994) en EE. UU., Rivera y Gómez (1991) en Colombia, Pérez y Senent (2015) en España y Saldaña et al. (2014) en Marruecos, han demostrado que existe una alta correlación entre el índice de erosividad de la lluvia R y el índice modificado de Fournier IMF, lo que confirma el resultado obtenido para la correlación entre R e IMF en la estación Aeropuerto de Managua.
Estación Jinotega
Utilizando las ecuaciones índice de erosividad de la lluvia (1), energía cinética total (2), y energía cinética unitaria de un tramo (3) se estimó Rt de cada tormenta para el período 1996-2015 y se obtuvieron los valores de erosividad de la lluvia de cada mes Rmes con la ecuación índice de erosividad de la lluvia en el mes (4). En la estación Jinotega los valores mensuales Rmes se presentan principalmente en los meses de mayo a octubre. Los otros meses del año no tienen valores significativos de R. Con la ecuación del índice modificado de Fournier (5) se calculó los valores de IMF mensuales. Las Figuras 2 (a y b) muestran las variaciones de R e IMF promedios mensuales, donde se puede observar que el índice IMF tiene una distribución bimodal dado que es función de las precipitaciones y que la erosividad R también sigue una distribución bimodal. Los máximos valores de R se presentan en los períodos más lluviosos del año, mayo-junio y septiembre-octubre; para el primer período el valor máximo se presenta en junio con un valor de 546 MJ ha-1 - mm h-1, y para el segundo período se presenta en octubre con un valor de 685 MJ ha-1 - mm h-1.
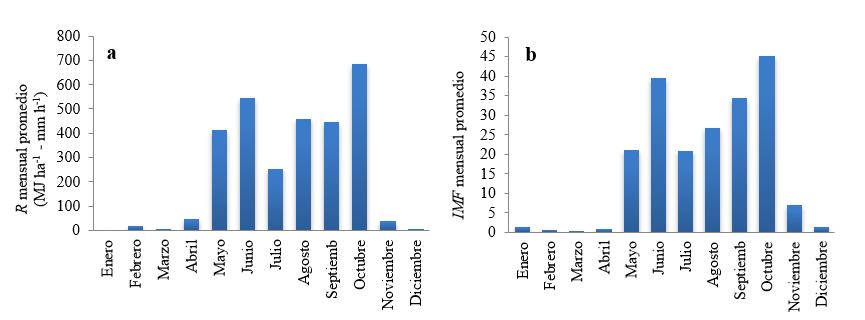
Se obtuvo la ecuación de correlación lineal para los datos índice de erosividad de la lluvia Rmese índice modificado de Fournier IMF mensual de la estación Jinotega, para el período 1996-2015. El coeficiente de determinación es r2 =0.74, indicando que hay una buena relación lineal entre las variables IMF mensual y R mensual. La ecuación de correlación obtenida es:
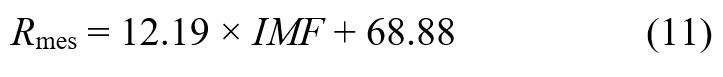
La ecuación de correlación (11) se utilizó para estimar los valores de R mensual del período de datos analizados, a estos los llamaremos "R estimado". A los valores R mensual calculados a partir de los datos pluviográficos y la ecuación (4), los llamaremos "R observado". Se procedió a correlacionar el valor R estimado con el valor R observado.
En el Cuadro 2 se muestra la comparación de los datos estadísticos de Rmes obtenidos en la estación Jinotega. Se puede ver que la ecuación de correlación (11) sobreestima el valor mínimo de Rmescon una diferencia de 54.9 MJ ha-1 - mm h-1, subestima el valor máximo por 64.3 MJ ha-1 - mm h-1, y subestima el valor medio, con una diferencia de 0.20 MJ ha-1 - mm h-1. La desviación estándar de Rmes estimado indica que el dato estimado varía menos alrededor de la media que el dato observado, con una diferencia de 71.6. Haciendo el análisis de desempeño de la ecuación de correlación (11) a través de los parámetros coeficiente de determinación r2 y porcentaje de sesgo PBIAS, el resultado de la estimación indica que el dato estimado es considera bueno para r2 (0.74), muy bueno para PBIAS (0.05 %), y bueno para MEF (0.51).
| Estadístico | R mensual observado | R mensual estimado | |
| Mínimo | 16.5 | 71.4 | |
| Máximo | 2 989.7 | 2 925.4 | |
| Medio | 415.9 | 415.7 | |
| Desviación estándar | 501.0 | 429.4 | |
| r2 | 0.74 | 71.4 | |
| PBIAS (%) | 0.05 | ||
| RMSE | 256.80 | ||
| MEF = RMSE/DesvStand | 0.51 | ||
| Cantidad de datos | 120 |
r2: coeficiente de determinación lineal, PBIAS: porcentaje de sesgo, RMSE:
raíz del error cuadrático medio, MEF: error cuadrático medio normalizado,
DesvStand: desviación estándar.
Autores como Arnoldus (1977) en Marruecos, Renard y Freidmund (1994) en EE. UU, Rivera y Gómez (1991) en Colombia, Pérez y Senent (2015) en España y Saldaña et al. (2014) en Marruecos, han demostrado que existe una alta correlación entre el índice de erosividad de la lluvia R y el índice modificado de Fournier IMF, lo que confirma el resultado obtenido para la correlación entre R e IMF en la estación Jinotega.
Estación Juigalpa
Utilizando las ecuaciones índice de erosividad de la lluvia (1), energía cinética total (2), y energía cinética unitaria de un tramo (3) se estimó Rt de cada tormenta para el período 1972-1991 y se obtuvieron los valores de erosividad de la lluvia de cada mes Rmes con la ecuación índice de erosividad de la lluvia en el mes (4). En la estación Juigalpa los valores mensuales Rmes se presentan principalmente en los meses de mayo a noviembre. Los otros meses del año no tienen valores significativos de Rmes. Con la ecuación del índice modificado de Fournier (5) se calculó los valores de IMF mensuales. Las Figuras 3 (a y b) muestran las variaciones de R e IMF promedios mensuales, y se observa que el índice IMF tiene una distribución bimodal dado que es función de las precipitaciones y que la erosividad R también sigue una distribución bimodal. Los máximos valores de R se presentan en los períodos más lluviosos del año, mayo-junio y agosto-octubre; para el primer período el valor máximo se presenta en junio con un valor de 752 MJ ha-1 - mm h-1, y para el segundo período se presenta en septiembre con un valor de 845 MJ ha-1 - mm h-1.
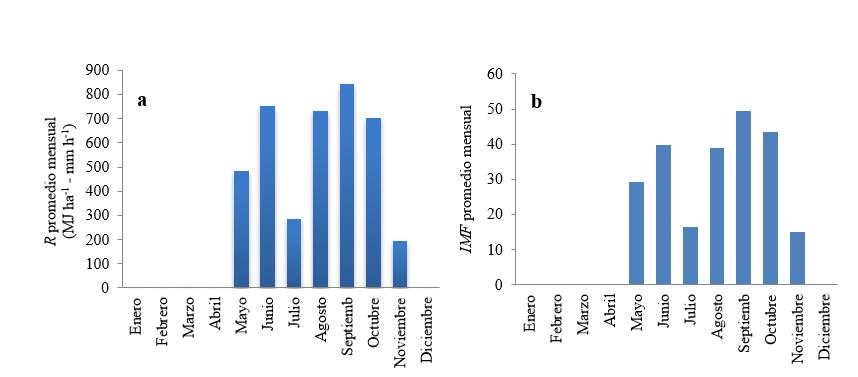
Se obtuvo la ecuación de correlación lineal para los datos índice de erosividad de la lluvia Rmese índice modificado de Fournier IMF mensual de la estación Juigalpa, para el período 1972-1991. El coeficiente de determinación es r2 = 0.78, indicando que hay una buena relación lineal entre las variables IMF mensual y R mensual. La ecuación de correlación obtenida es:
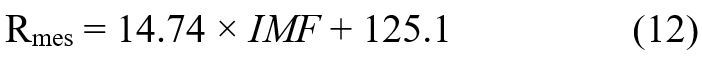
La ecuación de correlación (12) se utilizó para estimar los valores de R mensual del período de datos, a estos los llamaremos "R estimado". A los valores R mensual calculados a partir de los datos pluviográficos y la ecuación (4), los llamaremos "R observado".
En el Cuadro 3 se presenta la comparación de los datos estadísticos obtenidos de Rmes en la estación Juigalpa. Se puede ver qué la ecuación de correlación (12) sobreestima el valor mínimo de Rmescon una diferencia de 121.6 MJ ha-1 - mm h-1, subestima el valor máximo por 123.6 MJ ha-1 - mm h-1, y el valor medio fue casi igual al valor observado, con una diferencia de 0.10 MJ ha-1 - mm h-1. La desviación estándar de Rmes observado indica que el dato observado varía más alrededor de la media que el dato estimado, con una diferencia de 64.4. Haciendo el análisis de desempeño de la ecuación de correlación (12) a través de los parámetros coeficiente de determinación r2 y porcentaje de sesgo PBIAS, el resultado de la estimación indica que el dato estimado es considerado bueno para r2 (0.78) y muy bueno para PBIAS (0.03 %), y bueno para MEF (0.47).
| Estadístico | R mensual observado | R mensual estimado | |
| Min | 22.5 | 144.1 | |
| Max | 2 270.1 | 2 146.5 | |
| Medio | 596.2 | 596.1 | |
| Desviación Estándar | 538.6 | 474.2 | |
| r2 | 0.78 | ||
| PBIAS (%) | 0.03 | ||
| RMSE | 254.00 | ||
| MEF = RMSE/DesvStand | 0.47 | ||
| Cantidad de datos | 96 |
r2: coeficiente de determinación lineal, PBIAS: porcentaje de sesgo, RMSE: raíz
del error cuadrático medio, MEF: error cuadrático medio normalizado, DesvStand:
desviación estándar.
Otros autores como Arnoldus (1977) en Marruecos, Renard y Freidmund (1994) en EE. UU., Rivera y Gómez (1991) en Colombia, Pérez y Senent (2015) en España y Saldaña et al. (2014) en Marruecos, han demostrado que existe una alta correlación entre el índice de erosividad de la lluvia R y el índice modificado de Fournier IMF, lo que confirma el resultado obtenido para la correlación entre R e IMF en la estación Juigalpa.
Estación Rivas
Utilizando las ecuaciones índice de erosividad de la lluvia (1), energía cinética total (2), y energía cinética unitaria de un tramo (3) se estimó Rt de cada tormenta para el período 1970-1991 y se obtuvieron los valores de erosividad de la lluvia de cada mes Rmes con la ecuación índice de erosividad de la lluvia en el mes (4). En la estación Rivas los valores Rmes se presentan principalmente en los meses de mayo a noviembre. Los otros meses del año no tienen valores significativos de Rmes. Con la ecuación del índice modificado de Fournier (5) se calculó los valores de IMF mensuales. Las Figuras 4 (a y b) muestran las variaciones de R e IMF promedios mensuales, y se observa que el IMF tiene una distribución bimodal dado que es función de las precipitaciones y que la erosividad R también sigue una distribución bimodal. Los máximos valores de R se presentan en los períodos más lluviosos del año, mayo-junio y agosto-octubre; para el primer período el valor máximo se presenta en junio con un valor de 1 125 MJ ha-1 - mm h-1, y para el segundo período se presenta en septiembre con un valor de 1 013 MJ ha-1 - mm h-1.
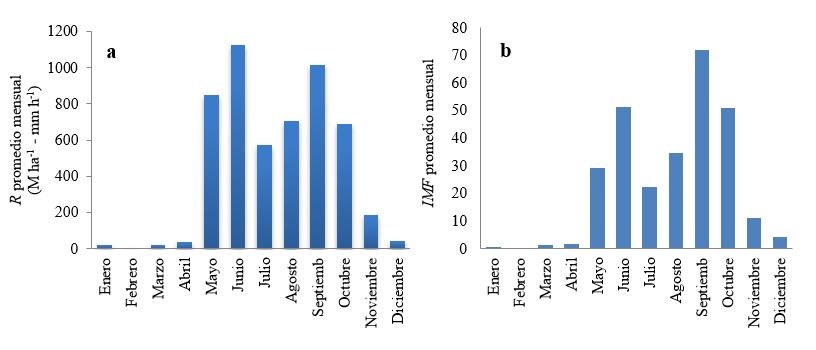
Se obtuvo la ecuación de correlación lineal para los datos índice de erosividad de la lluvia Rmes e índice modificado de Fournier IMF mensual de la estación Rivas, para el período 1970-1991. El coeficiente de determinación es r2 = 0.70, indicando que hay una buena relación lineal entre las variables IMF mensual y R mensual. La ecuación de correlación obtenida es:
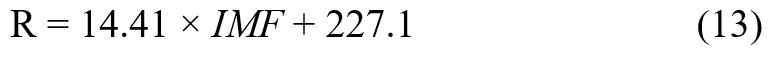
La ecuación de correlación (13) se utilizó para estimar los valores de R mensual del período de datos, a estos los llamaremos "R estimado". A los valores R mensual calculados a partir de los datos pluviográficos y (4), los llamaremos "R observado".
En el Cuadro 4 se muestra la comparación de los datos estadísticos obtenidos de Rmes para el período 1970-1991 en la estación Rivas. Se puede ver que la ecuación de correlación (13) sobreestima el valor mínimo de Rmes con una diferencia de 221.2 MJ ha-1 - mm h-1, subestima el valor máximo por 940.2 MJ ha-1 - mm h-1, y subestima el valor medio, con una diferencia de 0.10 MJ ha-1 - mm h-1. La desviación estándar de Rmes observado indica que el dato observado varía más alrededor de la media que el dato estimado, con una diferencia de 119.1. Haciendo el análisis de desempeño de correlación (13) a través de los parámetros coeficiente de determinación r2 y porcentaje de sesgo PBIAS, el resultado de la estimación indica que el dato estimado es considera bueno para r2 (0.70), muy bueno para PBIAS (0.01 %) y bueno para MEF (0.55).
| Estadístico | R mensual observado | R mensual estimado | |
| Min | 9.5 | 230.7 | |
| Max | 4 284.4 | 3 344.2 | |
| Medio | 718.5 | 718.4 | |
| Desviación Estándar | 723.7 | 604.6 | |
| r2 | 0.70 | ||
| PBIAS (%) | 0.01 | ||
| RMSE | 396.20 | ||
| MEF = RMSE/DesvStand | 0.55 | ||
| Cantidad de datos | 136 |
r2: coeficiente de determinación lineal, PBIAS: porcentaje de sesgo, RMSE:
raíz del error cuadrático medio, MEF: error cuadrático medio normalizado,
DesvStand: desviación estándar.
En las cuatro estaciones meteorológicas estudiadas se muestra una distribución bimodal de los R promedio mensual, debido a la distribución bimodal de las precipitaciones en Nicaragua. Este comportamiento bimodal del índice R ha sido descrito por Calero et al. (2021), en un estudio en el Valle del Cauca, Colombia, donde se utilizaron datos pluviográficos de 12 estaciones. También en el estudio de Ares et al. (2012) en Argentina, describe un comportamiento bimodal de la distribución de R.
En la estación del Aeropuerto de Managua el valor máximo promedio mensual de R es 1 323 MJ ha-1 - mm h-1 que ocurre en el mes de septiembre, y el segundo valor más alto es de 1 013 MJ ha-1 - mm h-1 en el mes de mayo (Figura 1a). En la estación de Jinotega el valor máximo promedio mensual de R es 685 MJ ha-1 - mm h-1 que ocurre en el mes de octubre, y el segundo valor más alto es de 546 MJ ha-1 - mm h-1 en el mes de junio (Figura 2a). En la estación de Rivas el valor máximo promedio mensual de R es 1 125 MJ ha-1 - mm h-1 que ocurre en el mes de junio y el segundo valor más alto es de 1 013 MJ ha-1 - mm h-1 en el mes de septiembre (Figura 4a). En la estación Juigalpa, en el departamento de Chontales, el valor máximo promedio mensual de R es 845 MJ ha-1 - mm h-1 que ocurre en el mes de septiembre, y el segundo valor más alto es de 752 MJ ha-1 - mm h-1 en el mes de junio (Figura 3a).
Se observa que hay variaciones espaciales en los valores del índice de erosividad de la lluvia, las que obedecen a las características climáticas de cada departamento donde se localizan las cuatro estaciones analizadas. Los autores Pérez y Senent (2015) en un estudio en España también encontraron esta variación espacial del índice R, asociada a los regímenes de lluvia por región climática. En Colombia Lince y Castro (2015) en un estudio en la región cafetera de Quindío también encontraron variaciones espaciales en el índice R, asociados a los regímenes de lluvia de los sitios estudiados.
En las cuatro estaciones meteorológicas analizadas se observó (Figuras 1 a 4) que cuando los valores del IMF se incrementan también se incrementan los valores de R, esto es debido a que cuando se incrementan las precipitaciones el IMF y el R también se incrementan. Esto da como resultado que la correlación de R y el IMF para el período de estudio tenga un coeficiente de determinación r2 ≥ 0.70, que es bueno.
En el análisis estadístico se logró obtener buenos resultados (Cuadros 1 a 4), los parámetros de evaluación coeficiente de determinación (r2), porcentaje de sesgo (PBIAS) y raíz del error cuadrático medio (RMSE) resultaron satisfactorios. Se han obtenido resultados similares en estudios realizados en Marruecos por Arnoldus (1977), en Colombia por Rivera y Gómez (1991), Lince y Castro (2015) y Calero Mosquera (2021); en EE. UU. por Renard y Freimund (1994), en Nicaragua por Blanco Chávez (2019) y Gutiérrez y Blanco Chávez (2021). Lo anterior nos permite afirmar que las ecuaciones de correlación (10), (11), (12) y (13) se podrían utilizar para la estimación de Rmes a partir del IMF mensual en aquellos sitios cercanos a las estaciones en estudio que sólo disponen de datos mensuales de precipitación.
CONCLUSIONES
El índice de erosividad mensual promedio (R) varía en función de las estaciones meteorológicas. En todas las estaciones se presentan valores picos en los períodos mayo-junio y septiembre-octubre, valores que se corresponden con la distribución de las precipitaciones en los departamentos de Managua, Rivas Jinotega y Chontales.
Las estaciones Aeropuerto de Managua y Rivas, presentan mayores valores picos del índice de erosividad mensual promedio que los valores obtenidos en las estaciones Jinotega y Juigalpa.
Según el índice modificado de Fournier (IMF) e índice de erosividad de la lluvia (Rmes) a escala mensual, indica que pueden ser usado en sitios cercanos a las estaciones estudiadas que cuentan con datos mensuales de precipitación.
REFERENCIAS BIBLIOGRÁFICAS
Ares, M. G., Varni, M. y Entraigas, I. (2012). Análisis estacional de la erosividad de las precipitaciones y la potencialidad de pérdida de suelo en la localidad de Azul (Provincia de Buenos Aires, Argentina). Cuadernos del CURIHAM, 18, 15-21. https://rephip.unr.edu.ar/bitstream/handle/2133/7152/An%C3%A1lisis%20estacional%20de%20la%20erosividad%20de%20las%20precipitaciones.pdf?sequence=3&isAllowed=y
Arnoldus, H. M. (1977). Methodology used to determine the maximum average soil loss due to sheet and rill erosion in Morocco. Assessing Soil Degradation. FAO.
Blanco Chávez, M. E. (2019). Factor Erosividad de la lluvia en la subcuenca Sur del lago Xolotlán, Managua. Nexo Revista Científica, 32(1), 41-51. https://doi.org/10.5377/nexo.v32i01.7986
Calero Mosquera, D., Martínez López, C. y Menjívar Flores, J. C. (2021). Evaluación de modelos para estimar la erosividad de la lluvia en el Valle del Cauca, Colombia. Acta Agronómica, 70(2), 198-210. https://doi.org/10.15446/acag.v70n2.95115
Gutiérrez, I. C. y Blanco Chávez, M. E. (2021). Erosión Hídrica Superficial en la microcuenca del río Mancotal en Jinotega, Nicaragua. Nexo, 34(2), 625-635. https://doi.org/10.5377/nexo.v34i02.11548
De Luis, M., González-Hidalgo, J. C., Raventos, J., Sánchez, J. R. y Cortina, J. (1997). Distribución espacial de la concentración y agresividad de la lluvia en el territorio de la comunidad Valenciana. Cuaternario y Geomorfología, 11, 33-44. http://tierra.rediris.es/CuaternarioyGeomorfologia/images/vol11_2/cuaternario11(3-4)_03_.pdf
Lince Salazar, L. A. y Castro Quintero, A. F. (2015). Erosividad de la lluvia en la región cafetera de Quindío, Colombia. Cenicafé, 66(1), 25-31. https://www.cenicafe.org/es/publications/3.Erosividad_25-31.pdf
Moriasi, D. N., Arnold, J. G., Van Liew, M. W., Bingner, R. L., Harmel, R. D. y Veith, T. L. (2007). Model Evaluation Guidelines for systematic quantification of accuracy in watershed simulations. TransASABE, 50(3), 885-900. https://doi.org/10.3390/10.13031/2013.23153https://elibrary.asabe.org/abstract.asp?aid=23153
Pérez, J. y Senent, J. (2015). Análisis comparativo de la evaluación de la erosividad de la lluvia en la cuenca del Guadalentín.http://www.ingenieriadelagua.com/2004/JIA/Jia2015/m/m011.pdf
Renard, K. G. y Freimund, J. R. (1994). Using monthly precipitation data to estimate the R factor. https://docplayer.es/91499309-Analisis-comparativo-de-la-evaluacion-de-la-erosividad-de-la-lluvia-en-la-cuenca-del-guadalentin.html
Renard, K. G., Foster, G. A., Geesies, G. A., Mc Cool, D. K. y Yoder, D. C. (1997). Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE). USDA.
Rivera, J. H. y Gómez, A. A. (1991). Erosividad de las lluvias en la zona cafetera central colombiana (Caldas, Quindío y Risaralda). Cenicafé, 42(2), 37-52. https://www.cenicafe.org/es/index.php/nuestras_publicaciones/revista_cenicafe/revista_cenicafe_arc042_02_37-52
Saldaña, M., Nemmaoui, A., Canton, M., Aguilar, M. y Aguilar, F. (2014). Estimación de la erosión potencial en la cuenca del río Moulouya aguas arriba de la Presa Mohamed V. Mapping, 23(168), 4-16. http://www2.ual.es/cooptrust/wp-content/uploads/2014/06/Art%C3%ADculo_Mapping.pdf
Wischmeier, W. H. y Smith, D. D. (1978). Predicting Rainfall Erosion Losses: A Guide to Conservation Planning. https://naldc.nal.usda.gov/download/CAT79706928/PDF
Zhong, X. y Dutta, U. (2015). Engaging Nash-Sutcliffe efficiency and model efficiency factor indicators in selecting and validating effective light rail system operation and maintenance cost models. Journal of Traffic and Transportation Engineering, 3, 255-265. https://doi.org/10.17265/2328-2142/2015.05.001
Notas de autor
Información adicional
Abreviaturas: RUSLE: ecuación
universal revisada de pérdida de suelo.
Abbreviation: RUSLE: Revised universal soil lost equation.

