



Recursos Naturales y Ambiente
Curvas de intensidad, duración y frecuencia derivada de lluvia máxima diaria a partir de datos de seis estaciones meteorológicas en Nicaragua
Intensity, duration and frequency curves derived of diary maximum rainfall from data of six meteorological stations, Nicaragua
La Calera
Universidad Nacional Agraria, Nicaragua
ISSN: 1998-7846
ISSN-e: 1998-8850
Periodicidad: Semestral
vol. 24, núm. 43, 2024
Recepción: 29 Abril 2024
Aprobación: 29 Octubre 2024
Resumen: En los sitios de proyectos de aprovechamiento de los recursos hídricos se requiere determinar las curvas intensidad, duración y frecuencia de lluvia para estimar caudales máximos. El objetivo de esta investigación fue estimar la correlación que hay entre la precipitación máxima diaria, las intensidades máximas para diferentes duraciones de lluvia, y los períodos de retorno, utilizando datos de lluvias de seis estaciones meteorológicas de la zona del Pacífico y zona Central del país. Se ha utilizado la función de distribución Gumbell para obtener las curvas intensidad, duración y frecuencia en las estaciones pluviográficas, para duraciones de cinco a 120 minutos. Con la prueba Smirnov-Kolmogorov, para un nivel de significancia de 5 %, se determinó que la función Gumbell tiene un buen ajuste con la probabilidad empírica de los datos analizados. Utilizando una relación potencial de las intensidades para diferentes duraciones, los períodos de retorno, y las precipitaciones máximas de 24 horas, se han obtenido ecuaciones que permiten estimar las curvas intensidad, duración y frecuencia (IDF) a partir de las precipitaciones máximas de 24 horas. Estas ecuaciones podrían ser utilizadas para estimar las curvas de intensidad, duración y frecuencia en sitios donde únicamente se dispone de datos de precipitaciones diarias en la zona de influencia de las seis estaciones meteorológicas.
Palabras clave: precipitación diaria, intensidad máxima, análisis de frecuencia, período de retorno.
Abstract: In the places of hydraulics resources facility, it is required to estimate the intensity-duration-frequency rainfall curves, in order to estimate the maximum discharges. The aim of this study was to estimate the correlations between the annual diary maximum precipitation, the maximum intensities for different rainfall durations, and the returns periods, using rainfall data of six meteorological stations from the Pacific and Central zones of the country. The Gumbell distribution has been used to obtain the intensity-duration-frequency curves for the pluviograph stations, for durations of five to 120 minutes. Using the Smirnov-Kolmogorov test, with a 5% significant level, it was determined that the Gumbell distribution has a good adjustment with the analyzed data's empirical probability. Using a potential relation for the intensities with different durations, the return periods, and the 24 h maximum precipitations, equations were developed to allow to estimate the intensity-duration-frequency curves from the 24 h maximum precipitations. These equations could be used to obtain the IDF curves in those places where only available dairy precipitations, in the six meteorological stations.
Keywords: Dairy precipitation, maximum intensity, frequency analysis, return period.
Las curvas intensidad, duración y frecuencia (IDF) son ampliamente utilizadas en los cálculos hidrológicos para el diseño de obras hidráulicas como alcantarillas, puentes, vertederos de presas, canales de drenaje pluvial, y en estudios de amenazas por inundaciones y erosión hídrica. Las curvas IDF sólo se puede obtener en estaciones meteorológicas que disponen de pluviógrafos, los cuales registran la precipitación acumulada a lo largo del tiempo, en un gráfico, donde se pueden hacer lecturas de la lluvia cada cinco minutos, y con eso estimar las intensidades. En Nicaragua la mayoría de las estaciones son pluviométricas, únicamente registran la precipitación total acumulada en 24 horas, por lo que en esos sitios no se dispone de información para la obtención de las curvas de intensidad, duración y frecuencia.
Campos (1978), como se citó en Torne Angulo, (2023), indica que cuando no hay registros horarios de lluvias, se proponen ecuaciones para estimar su intensidad con diferente duración a partir de las series de precipitación máxima en 24 horas, obteniendo buenos resultados.
Otros autores como Hassan El-Sayed (2017) en Egipto, Mejía Arrieta (2017) y Vargas y Díaz Granados (1998) en Colombia, determinaron ecuaciones que relacionan las intensidades máximas anuales y sus períodos de retorno con las precipitaciones máximas diarias, con coeficientes de determinación R2> 0.80. De igual manera en Turquía, Sen (2019), en la India, Basumatary y Sundar Sil (2017), presentaron modelos matemáticos para estimar las curvas IDF como función de la lluvia máxima diaria, obteniendo también buenos resultados.
Para el análisis de frecuencia de las intensidades máximas anuales de diferentes duraciones, se ha utilizado la función de distribución de probabilidad de valores extremos Tipo uno de Gumbell (Chow, 1953),porque se adapta bien a las distribuciones empíricas de probabilidad de eventos máximos de lluvias (Chow etal., 1988). También se utilizó la función Gumbell para el análisis de las series de precipitación máxima diaria, para obtener sus valores para diferentes períodos de retorno. Se comprobó la bondad del ajuste de la función Gumbell mediante la prueba Smirnov-Kolmogorov (Villón Béjar, 2006).
Tomando en cuenta la insuficiente cantidad de estaciones pluviográficas en amplias regiones del país, se dificulta la precisión en la estimación de las intensidades máximas, y por consiguiente los caudales máximos de diseño asociados; se hace necesario plantear procedimientos que permitan solventar esta limitación en los estudios hidrológicos que se realizan en dichas zonas del país.
El objetivo de este estudio fue determinar las ecuaciones potenciales que relacionan los datos de las curvas de intensidad, duración y frecuencia con las precipitaciones máximas de 24 horas, que nos permita estimar la intensidad, duración y frecuencia en aquellos sitios que únicamente disponen de datos diarios de precipitación, solventando así la escasa disponibilidad de datos pluviográficos para estimar las curvas intensidad, duración y frecuencia.
MATERIALES Y MÉTODOS
Análisis de independencia de las series de precipitación máxima diaria anual
Los supuestos del análisis de frecuencia de una serie de datos es que son aleatorios, que no dependen de los valores anteriores, garantizando así que son datos independientes. Para el análisis de independencia de las precipitaciones máximas de 24 horas, se utilizó el siguiente coeficiente de autocorrelación.
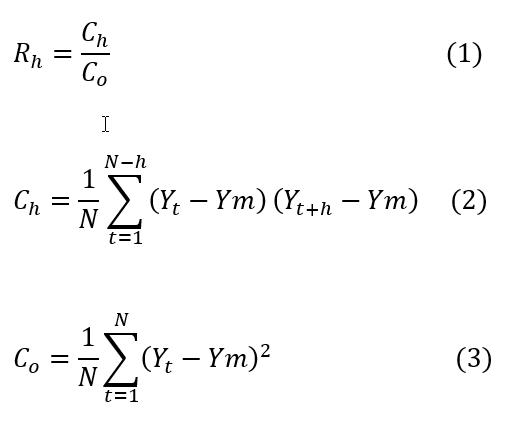
Donde:
Rh = Coeficiente de autocorrelación
Ch = Función de auto covarianza
Co = Función de varianza
h = Desfase en años
Yt = Valor de la intensidad de lluvia en el año t
Ym = Valor medio de la serie de intensidades de lluvia
N = Número de años de la serie de intensidades de lluvia.
El valor resultante de Rh oscilara entre -1 y +1.
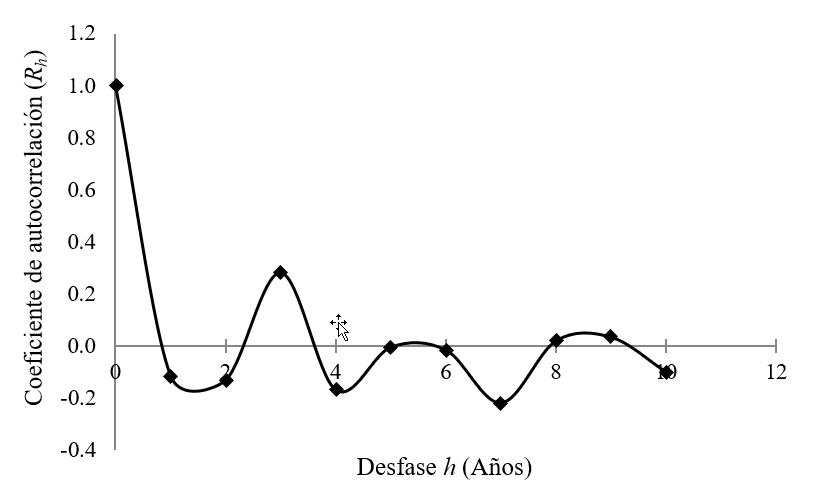
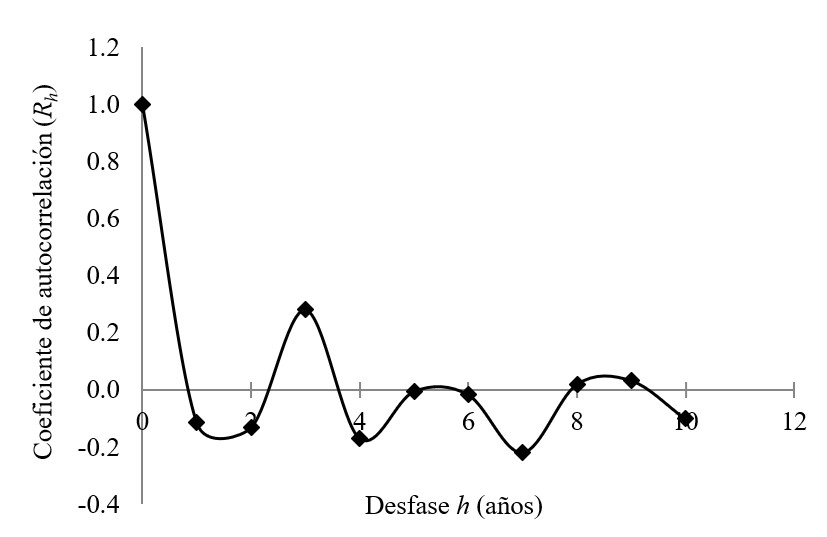
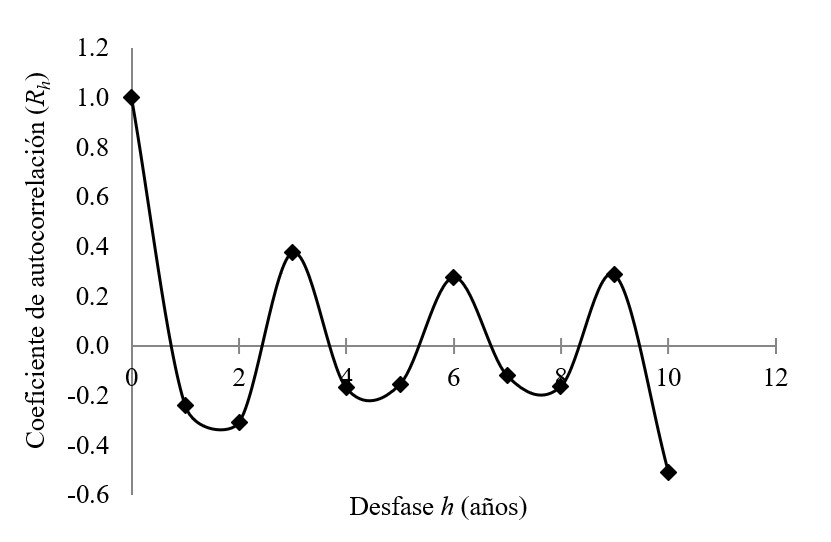
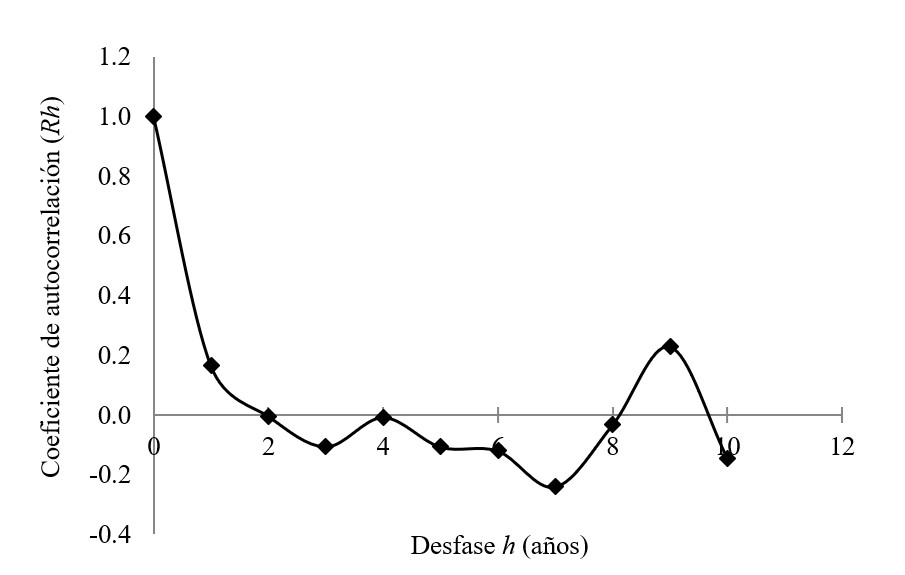
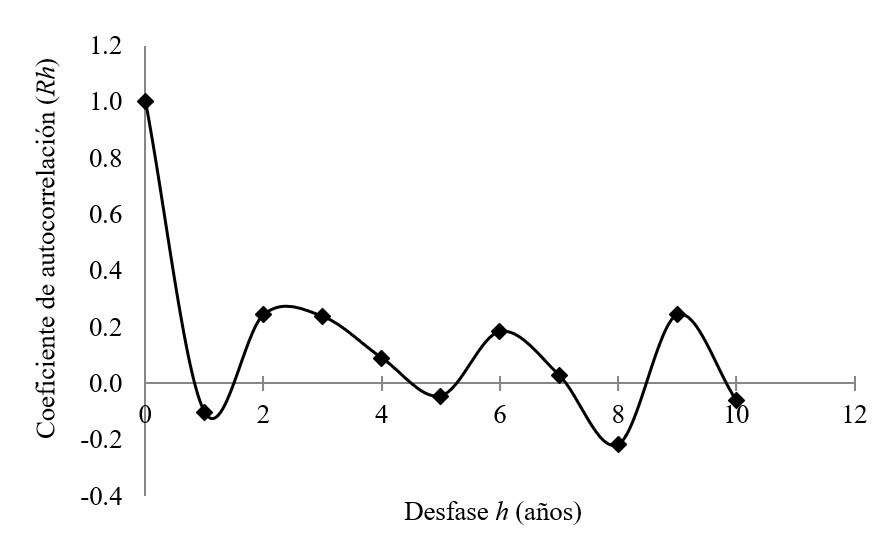
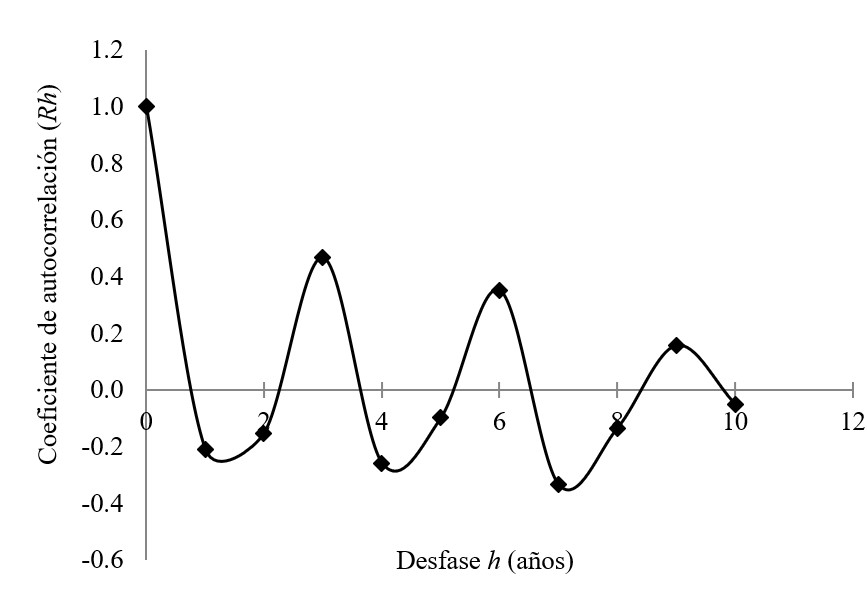
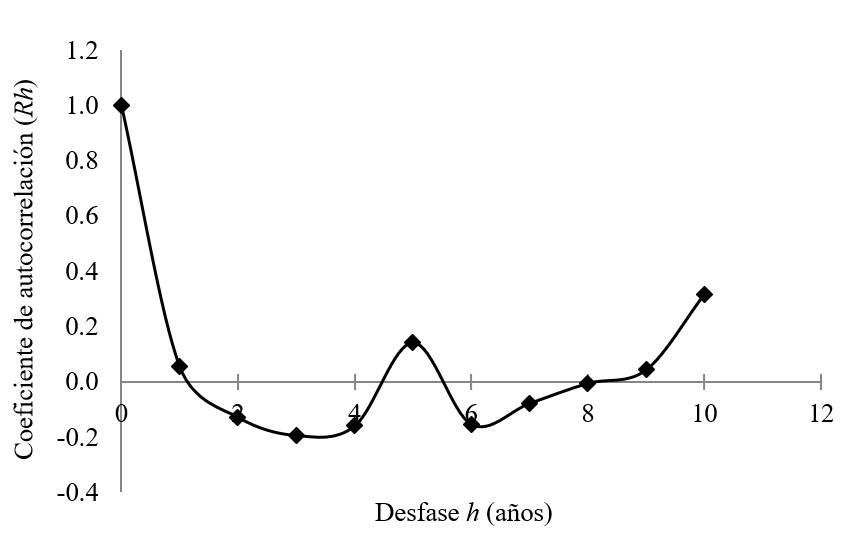
Con los valores del coeficiente de autocorrelación Rh, con desfase h desde cero a diez años, se procede a graficar el desfase contra Rh(Figura 1), obteniendo así el correlograma de la serie de precipitaciones máximas de 24 horas.
Cuando los valores de Rhse aproximan a cero, los valores de la serie no son autocorrelativos, es decir, el valor actual no depende del valor anterior, y se puede inferir que la serie es independiente.
Obtención de las curvas de intensidad, duración y frecuencia
Para obtener las curvas IDF se realizó el análisis de frecuencia con la función de probabilidad Gumbel (valores extremos tipo I), la que ajusta bien a las precipitaciones máximas anuales (Chow et al., 1988; Muñoz y Zamudio, 2018; Wilches et al., 2020).La función de distribución de probabilidad acumulativa para Valores Extremos Tipo I (EVI) es:
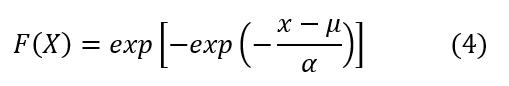
Para todo -α ≤ x ≤ α
Los parámetros de la función son estimados con:

Donde:
α = Parámetro de escala
μ= Parámetro de posición, llamado también moda de la distribución
S = Desviación estándar de la serie analizada x
Xmed = Media de la serie analizada x
Se puede definir una variable reducida:

Sustituyendo:
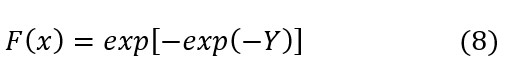
Despejando Y:
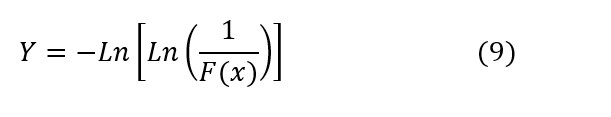
También se puede calcular con el período de retorno T la probabilidad acumulada p(x ≤ X):

Sustituyendo F(xT) en Y, se obtiene la variable YT:
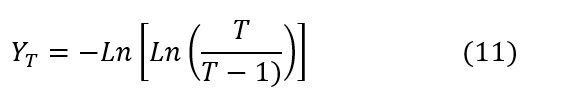
Para la distribución de Valores Extremos Tipo I (EVI), XT está relacionado con YT por medio de:
XT = μ + α YT (12)
Donde XT es valor máximo de la variable para un determinado período de retorno de la serie analizada.
Bondad del ajuste
Se revisó la bondad del ajuste de la distribución de probabilidad teórica de la función de Gumbell (EVI) a la distribución de probabilidad empírica de los datos de intensidades con la prueba de Smirnov-Kolmorov, en la que se compara las desviaciones máximas de la probabilidad de la función Gumbell respecto a la probabilidad empírica ΔPmax, con la desviación máxima de Smirnov-KolmogorovΔmax. En esta prueba se utilizó un nivel de significancia α de 5%. Para que se acepte el ajuste de la función Gumbell (EVI) se debe cumplir que ΔPmax ≤ Δmax (Villón Béjar, 2006).
La distribución de probabilidad empírica (Chow et al., 1988) se calculó con la fórmula de Weibull:
p=m/(N+1) (13)
Donde:
p = Probabilidad empírica
m = Número de orden de una serie ordenada de menor a mayor
N = Número total de datos de la serie
Correlación de las IDF a partir de precipitaciones máximas de 24 horas
Se utilizó una ecuación tipo exponencial propuesta por Vargas y Díaz Granados (1998) que plantea:

Donde:
I = Intensidad de precipitación en milímetros por hora (mmh-1).
T = Periodo de retorno en años, asociado a la intensidad I.
M = Precipitación máxima promedio anual en 24 horas (mm), a nivel multianual, para un determinado T
t = Duración de la lluvia en minutos
a, b, c y d = Parámetros de ajuste de la regresión
Para obtener los parámetros de la ecuación anterior se procedió a hacer una transformación de ecuación exponencial a una de tipo lineal, mediante la aplicación de logaritmos naturales a ambos lados de (14):
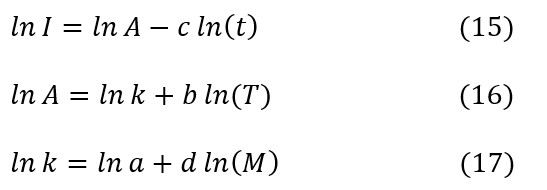
La aplicación de este artificio permite establecer una relación lineal entre los logaritmos de las variables, por lo que se puede aplicar la técnica de los mínimos cuadrados para determinar los valores óptimos de cada parámetro (Mejía Arrieta, 2017).
Se obtuvieron los coeficientes A y c de (15) por correlación lineal. Con el método de mínimos cuadrados se obtuvo la ecuación de la recta de mejor ajuste, usando como variable independiente X = ln (t) y variable dependiente Y = ln (I). Los valores A y c se obtuvieron para cada período de retorno en cada estación seleccionada. La calidad de esta correlación se evaluó mediante el coeficiente de determinación R2. La correlación lineal se realizó en una hoja de cálculo de Microsoft Excel.
Una vez obtenidos los valores de A de cada período de retorno especificado (T), se procedió a resolver (16), correlacionando la variable independiente X = ln (A) con la variable dependiente Y = ln (T), aplicando nuevamente el método de mínimos cuadrados, para la estimación de los coeficientes "k" y "b" respectivamente.
Una vez obtenidos los valores de k, y con los valores de la variable independiente M de cada período de retorno especificado, se procedió a resolver (17), correlacionando la variable X = ln (M) con la variable dependiente Y = ln (k), aplicando nuevamente el método de mínimos cuadrados, para la estimación de los coeficientes "a" y "d" respectivamente.
De esta forma quedaron determinados los coeficientes a, b, c, y d de (14), la cual permite obtener las intensidades máximas para duraciones de lluvia menores que 24 horas, para un determinado período de retorno.
Datos utilizados
Se utilizaron datos de seis estaciones meteorológicas, que disponían de series de intensidades máximas anuales para diferentes duraciones de lluvia, y las series de precipitaciones máximas anuales en 24 horas de duración. El Cuadro 1 muestra el nombre de las estaciones, el período de registro de información y el estado de la información según período de registro.
| Estación | Período | Período faltante |
| Managua Aeropuerto | 1971-2012 | Completo |
| Masaya Lagunas | 1977-2002 | Completo |
| Campos Azules | 1971-2001 | 1988-1992 |
| Rivas | 1975-2002 | Completo |
| Juigalpa | 1980-2001 | 1998 |
| Jinotega | 1975-2002 | 1998 |
RESULTADOS Y DISCUSIÓN
Se realizó la prueba de independencia de las series de precipitación máxima de 24 horas en las estaciones mediante el coeficiente de autocorrelación según la ecuación (1). Esto permitió obtener los correlogramas que se muestran de la Figuras 2 a la Figura 7.
En todas las series el correlograma muestra bajos valores del coeficiente de auto correlación Rh, indicando que los datos de las series no dependen de los datos de los años previos, esto es, la variable precipitación máxima de 24 horas es independiente o aleatoria, por lo que se pueden utilizar en el análisis de frecuencia con la función de distribución de valores extremos (EVI) de Gumbell. Esto se hace extensivo a las series de intensidades máximas con diferentes duraciones.
Para la obtención de las curvas IDF utilizando la función Gumbell (EVI), mediante el análisis de frecuencia se determinaron los parámetros de la ecuación (4), para las series de intensidades máximas y duraciones de lluvias de 5, 10, 15, 30, 60, 120 y 1 440 minutos. En el Cuadro 2 se indican los valores de dichos parámetros.
| Estación | Parámetro | Duración en minutos | ||||||
| 5 | 10 | 15 | 30 | 60 | 120 | 1440 | ||
| Managua Aeropuerto | α | 30.311 | 19.406 | 17.871 | 15.616 | 14.457 | 11.371 | 1.397 |
| µ | 140.398 | 117.716 | 97.489 | 67.827 | 43.022 | 23.423 | 3.160 | |
| Masaya Lagunas | α | 26.902 | 18.241 | 15.957 | 14.679 | 11.392 | 7.316 | 0.832 |
| µ | 130.453 | 106.179 | 89.928 | 66.962 | 44.013 | 25.512 | 2.298 | |
| Campos Azules | α | 15.350 | 10.350 | 11.744 | 10.058 | 10.506 | 5.803 | 0.992 |
| µ | 120.221 | 99.426 | 82.306 | 59.868 | 39.368 | 24.344 | 3.590 | |
| Rivas | α | 29.577 | 16.778 | 16.527 | 12.300 | 13.057 | 8.441 | 1.174 |
| µ | 123.271 | 99.166 | 86.261 | 63.283 | 43.171 | 24.221 | 3.802 | |
| Juigalpa | α | 33.692 | 18.242 | 15.930 | 14.205 | 8.877 | 7.387 | 1.040 |
| µ | 137.031 | 109.080 | 90.179 | 59.170 | 40.512 | 22.919 | 3.061 | |
| Jinotega | α | 29.867 | 23.100 | 20.303 | 13.072 | 8.203 | 6.308 | 0.864 |
| µ | 103.072 | 80.378 | 66.666 | 47.847 | 31.780 | 15.589 | 2.295 | |
Posteriormente se realizó la prueba de bondad del ajuste Smirnov-Kolmogorov a la función Gumbell ajustada a los datos de intensidades máximas anuales de cada estación. En el Cuadro 3 se muestran los valores de desviaciones máximas obtenidas para las intensidades y diferentes duraciones de lluvia (ΔP) y la desviación máxima permitida (Δ máximo) de la prueba Smirnov-Kiomogorov.
| Estación | Parámetro | Duración en minutos | ||||||
| 5 | 10 | 15 | 30 | 60 | 120 | 1 440 | ||
| Managua Aeropuerto | ΔP máx | 0.149 | 0.137 | 0.099 | 0.070 | 0.083 | 0.079 | 0.073 |
| Δ máx | 0.210 | 0.210 | 0.210 | 0.210 | 0.210 | 0.210 | 0.210 | |
| Masaya Lagunas | ΔP máx | 0.142 | 0.121 | 0.111 | 0.075 | 0.123 | 0.128 | 0.071 |
| Δ máx | 0.267 | 0.267 | 0.267 | 0.267 | 0.267 | 0.267 | 0.267 | |
| Campos Azules | ΔP máx | 0.176 | 0.188 | 0.105 | 0.157 | 0.104 | 0.098 | 0.177 |
| Δ máx | 0.267 | 0.267 | 0.267 | 0.267 | 0.267 | 0.267 | 0.267 | |
| Rivas | ΔP máx | 0.199 | 0.098 | 0.084 | 0.078 | 0.113 | 0.111 | 0.117 |
| Δ máx | 0.257 | 0.257 | 0.257 | 0.257 | 0.257 | 0.257 | 0.257 | |
| Juigalpa | ΔP máx | 0.179 | 0.173 | 0.240 | 0.155 | 0.110 | 0.094 | 0.102 |
| Δ máx | 0.284 | 0.284 | 0.284 | 0.284 | 0.284 | 0.284 | 0.284 | |
| Jinotega | ΔP máx | 0.157 | 0.118 | 0.123 | 0.104 | 0.060 | 0.082 | 0.058 |
| Δ máx | 0.262 | 0.262 | 0.262 | 0.262 | 0.262 | 0.262 | 0.262 | |
Se observa que las desviaciones máximas de la función Gumbell ΔP son menores que las desviaciones máximas de la prueba Smirnov-Kiomogorov Δ máximo, por lo que se acepta el ajuste de (4) a los datos de intensidades máximas de diferentes duraciones en las seis estaciones del estudio.
Una vez verificada la bondad del ajuste, se procedió a obtener las intensidades máximas anuales con (4) ajustada, para cada estación seleccionada y para diferentes períodos de retorno, las que se muestran desde el Cuadros 4 al Cuadro 9.
| T | Duración en minutos | ||||||
| 5 | 10 | 15 | 30 | 60 | 120 | 1 440 | |
| 5 | 185.86 | 146.82 | 124.30 | 91.25 | 64.71 | 40.48 | 5.26 |
| 10 | 208.61 | 161.39 | 137.71 | 102.97 | 75.56 | 49.01 | 6.30 |
| 15 | 221.44 | 169.60 | 145.27 | 109.58 | 81.68 | 53.82 | 6.90 |
| 20 | 230.43 | 175.35 | 150.57 | 114.21 | 85.96 | 57.20 | 7.31 |
| 50 | 258.67 | 193.44 | 167.22 | 128.76 | 99.43 | 67.79 | 8.61 |
| 75 | 271.06 | 201.37 | 174.53 | 135.14 | 105.34 | 72.44 | 9.18 |
| 100 | 279.83 | 206.99 | 179.70 | 139.66 | 109.53 | 75.73 | 9.59 |
| T | Duración en minutos | ||||||
| 5 | 10 | 15 | 30 | 60 | 120 | 1 440 | |
| 5 | 170.80 | 133.54 | 113.86 | 88.98 | 61.10 | 36.49 | 3.55 |
| 10 | 190.99 | 147.23 | 125.84 | 99.99 | 69.65 | 41.98 | 4.17 |
| 15 | 202.38 | 154.95 | 132.59 | 106.21 | 74.47 | 45.07 | 4.52 |
| 20 | 210.36 | 160.36 | 137.32 | 110.56 | 77.85 | 47.24 | 4.77 |
| 50 | 235.42 | 177.36 | 152.19 | 124.24 | 88.46 | 54.06 | 5.54 |
| 75 | 246.42 | 184.81 | 158.72 | 130.24 | 93.12 | 57.05 | 5.88 |
| 100 | 254.21 | 190.09 | 163.33 | 134.49 | 96.42 | 59.17 | 6.13 |
| T | Duración en minutos | ||||||
| 5 | 10 | 15 | 30 | 60 | 120 | 1 440 | |
| 5 | 143.25 | 114.95 | 99.92 | 74.95 | 55.13 | 33.05 | 5.08 |
| 10 | 154.76 | 122.72 | 108.73 | 82.50 | 63.01 | 37.40 | 5.82 |
| 15 | 161.26 | 127.10 | 113.71 | 86.76 | 67.46 | 39.86 | 6.24 |
| 20 | 165.81 | 130.17 | 117.19 | 89.74 | 70.57 | 41.58 | 6.54 |
| 50 | 180.12 | 139.81 | 128.13 | 99.11 | 80.36 | 46.99 | 7.46 |
| 75 | 186.39 | 144.04 | 132.93 | 103.22 | 84.66 | 49.36 | 7.87 |
| 100 | 190.83 | 147.04 | 136.33 | 106.13 | 87.70 | 51.04 | 8.15 |
| T | Duración en minutos | ||||||
| 5 | 10 | 15 | 30 | 60 | 120 | 1 440 | |
| 5 | 167.63 | 124.33 | 111.05 | 81.73 | 62.76 | 36.88 | 5.56 |
| 10 | 189.83 | 136.92 | 123.45 | 90.96 | 72.55 | 43.22 | 6.44 |
| 15 | 202.35 | 144.03 | 130.45 | 96.17 | 78.08 | 46.79 | 6.94 |
| 20 | 211.12 | 149.00 | 135.35 | 99.82 | 81.95 | 49.29 | 7.29 |
| 50 | 238.68 | 164.63 | 150.75 | 111.28 | 94.12 | 57.16 | 8.38 |
| 75 | 250.77 | 171.49 | 157.50 | 116.31 | 99.46 | 60.61 | 8.86 |
| 100 | 259.33 | 176.35 | 162.29 | 119.86 | 103.23 | 63.05 | 9.20 |
| T | Duración en minutos | ||||||
| 5 | 10 | 15 | 30 | 60 | 120 | 1 440 | |
| 5 | 187.57 | 136.44 | 114.07 | 80.48 | 53.83 | 34.00 | 4.62 |
| 10 | 212.85 | 150.13 | 126.03 | 91.14 | 60.49 | 39.54 | 5.40 |
| 15 | 227.12 | 157.85 | 132.77 | 97.15 | 64.25 | 42.67 | 5.84 |
| 20 | 237.10 | 163.26 | 137.49 | 101.36 | 66.88 | 44.86 | 6.15 |
| 50 | 268.50 | 180.26 | 152.34 | 114.60 | 75.15 | 51.74 | 7.12 |
| 75 | 282.27 | 187.72 | 158.85 | 120.41 | 78.78 | 54.76 | 7.54 |
| 100 | 292.02 | 192.99 | 163.46 | 124.52 | 81.35 | 56.90 | 7.84 |
| T | Duración en minutos | ||||||
| 5 | 10 | 15 | 30 | 60 | 120 | 1 440 | |
| 5 | 147.87 | 115.03 | 97.12 | 67.46 | 44.08 | 25.05 | 3.59 |
| 10 | 170.28 | 132.36 | 112.36 | 77.27 | 50.24 | 29.78 | 4.24 |
| 15 | 182.93 | 142.14 | 120.95 | 82.80 | 53.71 | 32.45 | 4.61 |
| 20 | 191.78 | 148.99 | 126.97 | 86.67 | 56.14 | 34.32 | 4.86 |
| 50 | 219.61 | 170.51 | 145.89 | 98.86 | 63.79 | 40.20 | 5.67 |
| 75 | 231.82 | 179.96 | 154.19 | 104.20 | 67.14 | 42.78 | 6.02 |
| 100 | 240.46 | 186.64 | 160.06 | 107.98 | 69.51 | 44.61 | 6.27 |
Con los datos de intensidades anteriores y las precipitaciones máximas promedios anuales en 24 h (M) se obtuvieron los parámetros a, b, c, y d de (14), auxiliándonos de (15), (16) y (17). Los Cuadros 10 y 11 muestran los parámetros obtenidos para cada estación en estudio.
| Estación | a | b | d |
| Managua Aeropuerto | 297.97 | 0.067 | 0.127 |
| Masaya Lagunas | 264.54 | 0.099 | 0.158 |
| Campos Azules | 202.55 | 0.047 | 0.206 |
| Rivas | 217.02 | 0.095 | 0.185 |
| Juigalpa | 309.82 | 0.107 | 0.138 |
| Jinotega | 255.19 | 0.145 | 0.159 |
| T | Managua Aeropuerto | Masaya Lagunas | Campos Azules | Rivas | Juigalpa | Jinotega |
| 5 | 0.475 | 0.470 | 0.450 | 0.455 | 0.533 | 0.555 |
| 10 | 0.448 | 0.459 | 0.429 | 0.440 | 0.524 | 0.549 |
| 15 | 0.436 | 0.454 | 0.419 | 0.433 | 0.519 | 0.547 |
| 20 | 0.428 | 0.450 | 0.413 | 0.429 | 0.516 | 0.545 |
| 50 | 0.408 | 0.441 | 0.395 | 0.417 | 0.508 | 0.541 |
| 75 | 0.401 | 0.438 | 0.389 | 0.413 | 0.505 | 0.540 |
| 100 | 0.396 | 0.436 | 0.384 | 0.410 | 0.504 | 0.539 |
En la correlación de las intensidades y las duraciones, de (15), se obtuvieron coeficientes de determinación R2 que variaron de 0.95 a 0.99, en la correlación del parámetro A y los períodos de retorno, de (16), se obtuvieron coeficientes de determinación R2 de 0.99, y en la correlación del parámetro k y las precipitaciones máximas de 24 horas, de (17), se obtuvieron coeficientes de determinación R2 de 0.97, como se puede ver en el Cuadro 12. Estos valores de R2 se consideran altos, y nos indican que se ha obtenido una buena correlación de las intensidades y las precipitaciones máximas de 24 horas.
| Ecuación | Estaciones | |||||
| Managua Aeropuerto | Masaya Lagunas | Campos Azules | Rivas | Juigalpa | Jinotega | |
| (15) | 0.98 - 0.99 | 0.976-0.977 | 0.955-0.975 | 0.97-0.98 | 0.99 | 0.97-0.98 |
| (16) | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| (17) | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 |
Estos resultados son comparables con los obtenidos por Vargas y Díaz (1998) en Colombia, quienes obtuvieron valores de R2 superior a 0.90, con excepción de la región del Caribe Colombiano donde en promedio fue de 0.73. De igual forma Mejía Arrieta (2017), en la región del Atlántico de Colombia, en un estudio para determinar curvas IDF a partir de precipitación máxima de 24 horas, obtuvo valores de R2 entre 0.95 y 0.99. En el sur de Turquía, Sen (2019) desarrolló ecuaciones para obtener curvas IDF a partir de precipitación máxima de 24 horas, con errores relativos menores del 10%.
Se resalta que los parámetros a, b y d no varían con el período de retorno (Cuadro 10). El parámetro a de las cuatro estaciones de la Zona del Pacífico varía de 200 a 298, con el mayor valor en la estación Managua Aeropuerto, en cambio para las dos estaciones de la Zona Central varía de 255 a 309. El parámetro b de las cuatro estaciones de la Zona del Pacífico varía de 0.047 a 0.099, con el mayor valor en la estación Masaya, en cambio para las dos estaciones de la Zona Central varía de 0.107 a 0.145. El parámetro d no tiene una tendencia específica para la Zona del Pacífico como en la Central, sus valores son similares, variando de 0.127 a 0.206, en cambio los parámetros a y b han mostrado que en la Zona Central se presentan sus mayores valores.
Los valores del parámetro c mostrados en el Cuadro 11, en general disminuyen al aumentar el período de retorno T, en la Zona del Pacífico se presentan sus valores más bajos, entre 0.384 y 0.475, en cambio en la Zona Central se presentan los valores más altos del parámetro c, que varían entre 0.504 y 0.555. Se ha evidenciado que hay una regionalización para los parámetros a, b y c de (14), la cual podría representar regímenes de precipitaciones diferentes de cada zona.
Finalmente se revisó la correlación de los datos de intensidades obtenidos con (12), la función Gumbell (Cuadros 4 al 9), con las intensidades obtenidas con (14) calibrada, obteniendo coeficientes R2 mínimos que varían entre 0.974 y 0.994 (Cuadro 13), los valores más altos corresponden a la estaciones Managua Aeropuerto cuyo R2= 0.988 (se analizó un registro de 42 años) y Juigalpa cuyo R2= 0.994 (se analizó un registro de 21 años), en cambio los valores más bajos corresponden a Jinotega cuyo R2= 0.974 (se analizó un registro de 27 años) y Campos Azules cuyo R2= 0.974 (se analizó un registro de 26 años). Estos resultados confirman que el ajuste obtenido para (14) representa adecuadamente las intensidades máximas anuales derivadas con la función Gumbell.
| Estación | Managua Aeropuerto | Masaya Lagunas | Campos Azules | Rivas | Juigalpa | Jinotega |
| R2 | 0.988 | 0.984 | 0.974 | 0.982 | 0.994 | 0.974 |
CONCLUSIONES
Es posible calibrar una ecuación que relacione las series de intensidades máximas anuales de una estación pluviográfica con la serie de precipitación máxima de 24 horas, obteniendo coeficientes de determinación altos, R2>0.97.
Los parámetros de la ecuación potencial de correlación de intensidades máximas anuales y precipitaciones máximas diarias a, b, y c, presentaron rangos de valores típicos para la Zona del Pacífico y Central del país, en cambio el parámetro d no presentó diferencias entre las dos regiones del país.
La ecuación ajustada con datos de intensidades de las seis estaciones con pluviógrafos permite obtener las curvas IDF para duraciones menores que 24 h, en las estaciones vecinas que sólo disponen de datos diarios de precipitación y que tienen régimen pluviométrico similar a las estaciones pluviográficas en estudio.
REFERENCIAS BIBLIOGRÁFICAS
Basumatary, V., & Sundar Sil, B. (2017). Generation of rainfall Intensity-Duration-Frequency curves for the Barak River basin. Meteorology, Hydrology and Water Management, 6, 1-11. http://www.mhwm.pl/pdf-79175-15962?filename=Generation%20of%20Rainfall.pdf
Campos, D. (1978). Cálculo de las curvas IDF a partir de registros de lluvia máxima en 24 horas y relaciones duración lluvia Promedio. Subdirección Regional Noreste de Obras Hidráulicas e Ingeniería Agrícola para el Desarrollo Rural.
Chow, V. T. (1953). Frequency analysis of hydrologic data with special application to rainfall intensities, bulletin 414. University of Illinois.
Chow, V. T., Maidment, D. y Mays, L. (1988). Hidrología aplicada. McGraw Hill.
Hassan El-Sayed, E. A. (2017). Development of synthetic rainfall distribution curves for Sinai area. Ain Shams Engineering Journal, 9(4), 1949-1957. https://doi.org/10.1016/j.asej.2017.01.010
Mejía Arrieta, B. S. (2017). Estimación de curva IDF a partir de lluvias máximas en 24 horas en el departamento del Atlántico [Tesis de grado, Universidad de la Costa]. Repositorio Institucional. https://hdl.handle.net/11323/238
Muñoz B., J.E. y Zamudio, H. E. (2018). Regionalización de ecuaciones para el cálculo de curvas de intensidad, duración y frecuencia mediante mapas de isolíneas en el departamento de Boyacá. Tecnura, 22(58), 53-64. https://doi.org/10.14483/22487638.14295
Sen, Z. (2019). Annual daily maximum rainfall-based IDF curve derivation methodology.Earth Systems and Environment, 3, 463–469. https://doi.org/10.1007/s41748-019-00124-x
Torne Angulo, L. M. (2023). Construcción de las curvas de intensidad, duración y frecuencia en el Municipio de Arjona, Bolívar (1999-2020) [Tesis de grado, Universidad de Cartagena]. Repositorio Digital. https://repositorio.unicartagena.edu.co/bitstream/handle/11227/16244/documento-final_corregido_20_f-1.pdf?sequence=1&isAllowed=y
Vargas, M. R. y Díaz Granados, D. M. (1998). Curvas Sintéticas Regionalizadas de Intensidad-Duración-Frecuencia para Colombia. Universidad de los Andes.
Villón Béjar, M. (2006). Hidrología estadística. Editorial Tecnológica de Costa Rica.
Wilches, F. J., Hernández Ávila, R., & Caballero Guerrero, A. R. (2020). IDF curves and maximum rainfall in 24 hours in the subregions of La Mojana and San Jorge in the northern Colombia. International Journal of Engineering Research and Technology, 13(10), 2884-2894. https://doi.org/10.37624/IJERT/13.10.2020.2884-2894
Notas de autor

