Eficacia del sistema computacional CoCoA para la organización del pensamiento oral y escrito
Effectiveness of the CoCoA computational system for the organization of oral and written thinking
Cliffor Jerry Herrera-Castrillo
Universidad Nacional Autónoma de Nicaragua. Centro Universitario Regional de Estelí. UNAN-Managua/CUR-Estelí, Nicaragua.
https://orcid.org/0000-0002-7663-2499
cliffor.herrera@unan.edu.ni
RECIBIDO
02/09/2024
ACEPTADO
11/11/2024
RESUMEN
En el contexto actual dominado por la era digital, los sistemas computacionales se han establecido como una herramienta fundamental en diversos ámbitos de la comunicación humana, abarcando desde la programación hasta el desarrollo de inteligencia artificial y asistentes virtuales. El objetivo del estudio fue analizar cómo el Sistema de Álgebra Computacional CoCoA influye en la estructuración del discurso verbal y escrito de estudiantes de Matemáticas de la Universidad Nacional Autónoma de Nicaragua, Managua (UNAN-Managua) en su Centro Universitario Regional de Estelí (CUR-Estelí). Utilizando un enfoque mixto, descriptivo y transversal, donde se aplicaron encuestas a una muestra de 13 estudiantes y 8 profesores. Los resultados revelaron una percepción positiva entre los estudiantes, quienes valoran CoCoA por su capacidad para fortalecer habilidades de pensamiento computacional y facilitar la resolución de problemas matemáticos complejos. Sin embargo, se identificó una brecha significativa: muchos docentes carecen de conocimientos suficientes sobre esta herramienta. Esta disparidad subraya la urgencia de implementar programas de formación docente para integrar efectivamente CoCoA en el currículo educativo, promoviendo así un uso más equitativo y beneficioso de esta tecnología en el aprendizaje de las matemáticas. En conclusión, CoCoA representa una oportunidad crucial para mejorar tanto la comprensión como la expresión del pensamiento matemático, pero su implementación exitosa requiere un compromiso firme de las instituciones educativas para cerrar la brecha digital y maximizar su impacto educativo.
PALABRAS CLAVES
Tecnología educativa; sistema computacional; matemáticas; formación docente; pensamiento computacional.
ABSTRACT
In the current context dominated by the digital era, computational systems have established themselves as a fundamental tool in various fields of human communication, ranging from programming to the development of artificial intelligence and virtual assistants. The objective of the study was to analyze how the Computer Algebra System CoCoA influences the structuring of verbal and written discourse of Mathematics students at the National Autonomous University of Nicaragua, Managua (UNAN-Managua) in its Regional University Center of Estelí (CUR-Estelí). Using a mixed, descriptive and cross-sectional approach, where surveys were applied to a sample of 13 students and 8 professors. The results revealed a positive perception among students, who value CoCoA for its ability to strengthen computational thinking skills and facilitate the resolution of complex mathematical problems. However, a significant gap was identified: many teachers lack sufficient knowledge about this tool. This disparity underscores the urgency of implementing teacher training programs to effectively integrate CoCoA into the educational curriculum, thus promoting a more equitable and beneficial use of this technology in mathematics learning. In conclusion, CoCoA represents a crucial opportunity to improve both the understanding and expression of mathematical thinking, but its successful implementation requires a firm commitment from educational institutions to bridge the digital divide and maximize its educational impact.
KEYWORDS
Educational technology; computational system; mathematics; teacher training; computational thinking.
INTRODUCCIÓN
En la era digital actual, los sistemas computacionales están desempeñando un papel fundamental en diversas áreas de la comunicación humana, como en la programación, inteligencia artificial y asistentes virtuales, lo que hace necesario más estudios sobre ellos. Uno de los avances más destacados en este campo es el desarrollo del programa CoCoA (Computations in Commutative Algebra [Cálculos en álgebra conmutativa]), una herramienta que utiliza algoritmos avanzados para facilitar la organización del pensamiento tanto en expresión oral como escrita, a través de la simplificación de cálculos en el campo del álgebra.
Según Duque et al. (2002) CoCoA es un sistema algebraico computacional desarrollado en la Universidad de Génova, Italia. Diseñado para realizar cálculos en álgebra conmutativa, utiliza el algoritmo de Buchberger para el cómputo de bases de Gröbner y una variación para el cómputo de zizigias. Con un protocolo de bajo nivel, independiente de la arquitectura, CoCoA interactúa con los usuarios. Además, ofrece herramientas para el manejo de vectores y matrices, convirtiéndose en una herramienta versátil para resolver problemas matemáticos.
La organización efectiva del pensamiento oral y escrito desempeña un papel crucial en la enseñanza de las Matemáticas en educación superior. En este contexto, Solórzano Rojas et al. (2015) y Bernal Párraga et al. (2024) indican que la herramienta CoCoA, está basada en la disciplina de la informática surgiendo como un recurso potencial para mejorar esta habilidad cognitiva en los estudiantes.
Sin embargo, existen aspectos que aún se desconocen del uso de CoCoA en la literatura, ya que es visto como una herramienta complicada y de difícil comprensión en ocasiones confundida con “cocoa” lenguaje de programación para entornos del sistema operativo de Apple (iOS) (Valero Avilés, 2022), lo que crea vacíos de conocimiento significativos. A esto se le suma la falta de evaluaciones comparativas, la comprensión insuficiente en el aprendizaje, la escasez de investigaciones, sobre esta temática, en diferentes niveles educativos y la necesidad de una formación docente adecuada.
En la carrera de licenciatura en Ciencias de la Educación con mención en Matemáticas de la UNAN-Managua/CUR-Estelí, los estudiantes se enfrentan a varios retos al desarrollar el pensamiento algorítmico, que va de la mano con el análisis lógico matemático. Según Posso Domínguez & Murcia Londoño (2023), estas dificultades son serias y notables al intentar comprender los conceptos utilizados en la programación de computadoras, dado que el estudiantado se enfrenta a la complejidad de escribir códigos y comunicarse al compilar en el sistema de algebra computacional CoCoA.
Por ello, este estudio es conveniente y relevante desde varias perspectivas. Al integrar CoCoA en el proceso enseñanza-aprendizaje, mediante la aplicación de pruebas con estudiantes de la carrera de Matemáticas, esto fortalece la habilidad del estudiantado para organizar sus pensamientos de forma coherente al hablar, lo que les proporciona beneficios en su desarrollo académico y futuro como profesionales. Además, se promueve la colaboración docente-estudiante e investigadores, estimulando la creación de ideas nuevas y soluciones más efectivas en diferentes áreas del álgebra conmutativa.
Este artículo aporta conocimientos teóricos significativos al ser uno de los pocos escritos en habla hispana que aborda el uso del programa CoCoA en el desarrollo de habilidades cognitivas. Este enfoque enriquece el campo de la lingüística aplicada y la pedagogía al mejorar las habilidades comunicativas y la organización del pensamiento.
CoCoA, como herramienta práctica, es beneficiosa para el Ministerio de Educación de Nicaragua (MINED), las universidades y los grupos de docentes. Su implementación en la enseñanza de las Matemáticas como indican Solórzano Rojas et al. (2015) mejora el desarrollo de habilidades cognitivas y la aplicación de conceptos matemáticos en situaciones prácticas. Además, CoCoA permite una evaluación objetiva y una retroalimentación personalizada, lo que facilita un seguimiento más preciso del progreso de los estudiantes. Estos aspectos contribuyen a mejorar la calidad de la educación y enriquecer las prácticas pedagógicas de los docentes, adaptándose a las necesidades individuales del educando.
Se han tomado en cuenta varios antecedentes en el ámbito de los programas informáticos, la utilización de CoCoA y el fomento del pensamiento oral y escrito. Aunque estos elementos no se han abordado conjuntamente, se han encontrado investigaciones anteriores que tratan al menos una de estas variables de interés.
Estudios previos demuestran la importancia de desarrollar habilidades de organización del pensamiento en el aprendizaje de la matemática en la programación, se exploran diferentes enfoques y herramientas para mejorar esta competencia en los estudiantes (Galeano Caicedo, 2024; Fernández Cabrera, 2023). Sin embargo, aún existe una brecha en la literatura en cuanto a la evaluación específica de la incidencia del sistema computacional algebraico CoCoA en la organización del pensamiento oral y escrito, principalmente en las bases de Gröbner (Palacios Almendros, 2023).
También, se han realizado estudios sobre el fortalecimiento de las habilidades de computacionales utilizando la metodología STEAM (Science, Technology, Engineering, Arts and Mathematics [Ciencia, Tecnología, Ingeniería, Artes y Matemáticas]), a través de diferentes herramientas tecnológicas de uso habitual, para el fortalecimiento de competencias comunicativas y desarrollo del pensamiento computacional. Estos trabajos no toman el uso de sistemas de computación algebraicos, pero si, como estos influyen en la formación de los estudiantes y su contribución en otras áreas como la robótica e inteligencia artificial (Restrepo Pineda, 2024; Marín Romero & Rojas Martínez, 2023; Pantoja-Oñate, 2022; González-Fernández et al., 2021).
En el ámbito nacional, se ha trabajado sobre el lenguaje de categorías, algoritmos y esquemas iterativos que permiten obtener fórmulas nuevas en ecuaciones no lineales y de Adomian, donde se utiliza el programa Python, de manera mecánica. También, se ha abordado la resolución de sistemas de ecuaciones polinomiales utilizando las Bases de Gröbner y el Método de Autovalores, manipulando CoCoA solo para verificar la solución de problemas básicos (Herrera-Castrillo, 2024; Herrera Herrera & Cisneros Díaz, 2022; Méndez López & Cisneros Díaz, 2022; Solórzano Rojas et al., 2015).
Estos antecedentes demuestran que, si bien existen investigaciones previas que exploran aspectos relacionados con los programas computacionales, el desarrollo del pensamiento oral y escrito, y la mejora de habilidades comunicativas, aún se requiere una evaluación específica del uso de CoCoA en la organización del pensamiento oral y escrito.
En términos de tendencias educativas, se observa un creciente interés por la integración de tecnologías informáticas para mejorar las habilidades comunicativas. Se están adoptando enfoques metodológicos innovadores y herramientas tecnológicas para promover tanto la expresión oral como escrita, para fomentar el pensamiento computacional entre los estudiantes. No obstante, la evaluación específica de CoCoA en cuanto a su capacidad para organizar el pensamiento oral y escrito se considera un área de investigación emergente con un gran potencial para aportar al campo de la educación y la lingüística computacional.
Como plantean Mendoza Arenas et al. (2023) y Motoa (2019) el pensamiento computacional se enfoca en formar a los estudiantes como productores de tecnología en lugar de meros consumidores. Sin embargo, se reconoce la falta de una definición clara y un marco conceptual sólido para este concepto, así como la falta de debate sobre su contribución a los en educación y las implicaciones que puede tener en ciencias económicas e ingenierías (Adell Segura et al., 2019).
Además, se resalta la conexión que permite mejorar la calidad educativa al abordar las complejidades de la realidad contemporánea, especialmente en un entorno influenciado por las tecnologías de la información y la comunicación (Balladares Burgos et al., 2016). Esta integración de las TIC en la educación ofrece nuevas oportunidades para enriquecer los procesos de enseñanza-aprendizaje, permitiendo a los estudiantes desarrollar habilidades fundamentales para enfrentar los desafíos del mundo actual.
Siendo la Lingüística Computacional, para Casado-Mancebo (2022) un campo de estudio, que se enfoca en utilizar la informática y la inteligencia artificial para analizar y procesar el lenguaje natural. CoCoA es una herramienta que se enmarca en este enfoque y se utiliza para mejorar la organización del pensamiento en la forma de expresión oral y escrita. Al combinar las técnicas y algoritmos de la Lingüística Computacional, CoCoA permite una mejor comprensión y estructuración del lenguaje, facilitando la comunicación efectiva y el desarrollo de habilidades lingüísticas.
Por ello, la organización del pensamiento, de acuerdo con Vásquez Acevedo et al. (Vásquez Acevedo et al., 2023) y Sánchez-Camacho & Grane (2023) buscan enseñar a los estudiantes habilidades analíticas relacionadas con la informática y la programación. Esto implica fomentar la capacidad de estructurar y ordenar la información de manera lógica y coherente, de manera oral y escrita.
Asimismo, se consideran elementos como la coherencia y cohesión textual, que contribuyen a garantizar que las ideas se comuniquen de manera clara y comprensible. En conjunto, estos enfoques buscan desarrollar habilidades de pensamiento crítico y analítico en los estudiantes, brindándoles herramientas para expresarse de manera efectiva en diferentes contextos.
El aprendizaje de las Matemáticas y la Programación en la educación superior es esencial debido a su aplicabilidad en varias disciplinas, su capacidad para fomentar el pensamiento crítico y analítico, y su relevancia en el mercado laboral actual (Medina-Hernández et al., 2022). Estas habilidades brindan a los estudiantes las herramientas necesarias para abordar problemas complejos, realizar análisis de datos y tomar decisiones informadas. Además, el dominio de estas disciplinas les proporciona una ventaja competitiva en un mundo laboral cada vez más tecnológico.
Además de CoCoA, otros sistemas computacionales destacados en Matemáticas incluyen Mathematica, Maple y SageMath. Mathematica es ampliamente utilizada en ciencias e ingeniería, facilitando tareas de cálculo simbólico, aprendizaje automático y visualización de datos complejos. Maple, con su potente motor de cálculo y una interfaz intuitiva, apoya el análisis y la resolución de problemas en investigación y educación. SageMath, gratuito y de código abierto, integra herramientas como NumPy y SciPy en un entorno basado en Python, permitiendo un trabajo interactivo mediante línea de comandos o cuadernos web (Mantilla & Olaya-León, 2022; Pulido Rodriguez & López Bautista, 2022; Stein, 2011).
Por todo lo anterior, el objetivo de este artículo es analizar cómo el sistema computacional CoCoA influye en la estructuración del discurso verbal y escrito de estudiantes de matemáticas a nivel superior.
MATERIALES Y MÉTODOS
Tipo de estudio
De acuerdo con la profundidad del objeto de estudio, es descriptiva como señalan Fonseca Gómez (2023) y Valle Taiman et al. (2022) este tipo de estudio se caracteriza por proporcionar una descripción detallada de los fenómenos investigados, sin realizar inferencias causales o establecer relaciones de causalidad. Busca determinar si el uso de CoCoA puede mejorar la estructuración y claridad en la expresión de ideas, tanto en el lenguaje hablado como en el escrito.
Este estudio adopta un enfoque mixto, combinando datos cuantitativos y cualitativos. Al utilizar este diseño de investigación, se busca obtener una visión más completa y enriquecedora de los fenómenos investigados. El enfoque mixto permite abordar tanto aspectos numéricos y estadísticos como interpretaciones y descripciones detalladas de las experiencias y percepciones de los participantes. La integración de estos dos tipos de datos fortalece la validez y confiabilidad de los resultados, ya que los hallazgos pueden explorarse y validarse desde diferentes perspectivas y contextos (Sánchez et al., 2022; Itcara Palacios, 2014).
Por último, este estudio es de corte transversal, como plantean Manterola et al. (2023) esta investigación se caracteriza por la recopilación de datos de una población en estudio, en un lugar y momento determinado. En consecuencia, no hay una dimensión temporal implicada, ya que todos los datos se recopilan en el momento pertinente o en torno a este. En el caso de esta investigación, se está realizando en el trimestre de abril a junio 2024.
Área de estudio
El estudio se desarrolló en el Centro Universitario Regional de Estelí, perteneciente a la Universidad Nacional Autónoma de Nicaragua, Managua. Esta institución se encuentra ubicada en el barrio 14 de Abril, al noroeste de la ciudad de Estelí, cerca de la subestación de ENATREL. El Centro Universitario Regional de Estelí cuenta con cinco recintos universitarios, pero las oficinas principales, desde donde se gestionan los procesos administrativos y académicos de toda la institución, se ubican en el Recinto Leonel Rugama Rugama (Triminio-Zavala et al., 2024).
Población y muestra
Los elementos accesibles o unidad de análisis se refieren a los componentes o partes que pertenecen y se encuentran dentro del ámbito o contexto espacial donde se lleva a cabo el estudio o la investigación (Condori-Ojeda, 2020). En el presente artículo, la población consistió en 50 estudiantes de II a IV año de la carrera de Matemáticas y 15 docentes de la UNAN-Managua/CUR-Estelí, que facilitan componentes en dicha carrera.
La muestra, entendida como la parte representativa de la población (Condori-Ojeda, 2020), en este estudio estuvo compuesta por 13 estudiantes de IV y V año de la carrera de Matemáticas. Estos fueron seleccionados como la unidad de análisis, ya que representan de manera significativa a la población de interés para los propósitos de esta investigación. En el caso de los docentes se trabajó con 8 que son los que facilitan temáticas de álgebra o computación.
El muestreo utilizado en este estudio fue de tipo no probabilístico, lo que significa que no se emplearon métodos estadísticos para calcular la muestra. En lugar de ello, se utilizó un muestreo por conveniencia, donde el investigador seleccionó a los participantes según su propio criterio y conveniencia, sin seguir un procedimiento aleatorio. Por lo tanto, los resultados obtenidos a partir de esta muestra no pueden ser generalizados a una población más amplia (Hernández González, 2021).
Criterios de inclusión/ exclusión
Tabla 1
Criterios de inclusión, exclusión y eliminación
| Muestra de estudiantes | ||
|---|---|---|
| Inclusión | Exclusión | Eliminación |
| Estudiantes de la carrera de Matemáticas que hayan recibido al menos un componente de tecnología, ya sea en el laboratorio de Matemáticas u otro. | Estudiantes de Matemáticas que no hayan visto al menos 4 componentes de álgebra. | Estudiantes de Matemáticas que hayan tenido más de 4 inasistencias en el primer semestre del año 2024. |
| Muestra de docentes | ||
| Inclusión | Exclusión | Eliminación |
| Haber facilitado al menos un componente de álgebra o computación entre el II semestre de 2023 y el I semestre de 2024. Ser especialistas en Matemáticas o Física-Matemáticas. | Maestros que no cuenten con una especialización en Matemáticas o Física-Matemáticas. | Maestros que renuncien o sean despedidos de la institución durante el período del estudio. |
Para realizar este estudio se aplicó el proceso de consentimiento informado, con base a la siguiente ruta:
- Información al participante: Al participante se le ha seleccionado para participar en este estudio, se le indican los objetivos de la investigación.
- Comprensión del participante: Se le ha dado la oportunidad al participante de hacer preguntas y se han aclarado todas sus dudas sobre el estudio.
- Voluntariedad
- Autorización: Al dar su consentimiento verbal de participar en el estudio.
- Confidencialidad: Se le ha informado al participante sobre las medidas que se tomarán para proteger la confidencialidad de su identidad y la información que proporcione. Sus datos personales y resultados se mantendrán en estricta reserva.
Instrumentos para la recolección de la información
La recolección de datos es una etapa fundamental en el proceso de investigación, ya que implica la reunión y medición de información procedente de diversas fuentes, con el propósito de obtener una visión integral del fenómeno bajo estudio (Sánchez Martínez, 2022).
Tabla 2
Técnicas, instrumentos y fuentes de información
| Técnica | Definición | Instrumento | Fuentes |
|---|---|---|---|
| La encuesta | Con esta técnica de recolección de datos da lugar a establecer contacto con las unidades de observación por medio de los cuestionarios previamente establecidos (Tamayo & Silva, 2012). | Guía de encuesta online | Estudiantes de Matemática |
| La entrevista | La entrevista es una situación de interrelación o diálogo entre personas, el entrevistador y el entrevistado (Tamayo & Silva, 2012). | Guía de entrevista semiestructurada online | Docentes de la carrera de Matemáticas |
Etapas de la investigación
Las etapas que se siguieron para este trabajo fueron:
- Planificación: En esta primera etapa, se definió el problema de investigación, se realizó una exhaustiva revisión de la literatura existente sobre el tema, se establecieron los objetivos y se seleccionó el diseño metodológico más apropiado para abordar la problemática planteada.
- Trabajo de campo: Durante esta fase, se llevó a cabo la recolección de datos, a través de entrevistas y cuestionarios. Toda la información obtenida fue cuidadosamente registrada, ordenada y sistematizada para su posterior análisis.
- Análisis de datos: Una vez recolectada la información, se procedió a procesar y organizar los datos. Posteriormente, se realizó el análisis estadístico y cualitativo, según correspondiera, para interpretar los resultados y hallazgos obtenidos. Finalmente, se contrastaron estos resultados con la literatura revisada en la etapa de planificación.
- Devolución de resultados: Como etapa final, se llevó a cabo la divulgación de los resultados del estudio. Esto incluyó la publicación del artículo científico en una revista especializada y la socialización de los hallazgos con la comunidad académica. Además, se realizó una sesión de trabajo donde se presentaron y discutieron los resultados, como parte de un proceso de devolución y retroalimentación.
RESULTADOS Y DISCUSIÓN
Este estudio se llevó a cabo con estudiantes y docentes de Matemáticas de la UNAN-Managua/CUR-Estelí. La institución se caracteriza por hacer uso de tecnologías en los procesos de enseñanza-aprendizaje. En este contexto, se analizó la influencia del sistema computacional CoCoA en la estructuración del discurso verbal y escrito del estudiantado.
Uso de CoCoA
Los gráficos presentados a continuación muestran, por un lado, los resultados de la encuesta aplicada a los estudiantes sobre la influencia del CoCoA en su discurso oral. Por otro lado, se incluyen los hallazgos relacionados con el efecto de esta herramienta tecnológica en la estructuración de sus trabajos escritos. Estos datos se complementan con la información recopilada a través de las entrevistas realizadas a los docentes, lo que permite obtener una visión integral del fenómeno estudiado.
Figura 1
Familiaridad con el Lenguaje Computacional CoCoA
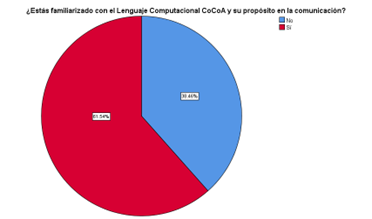
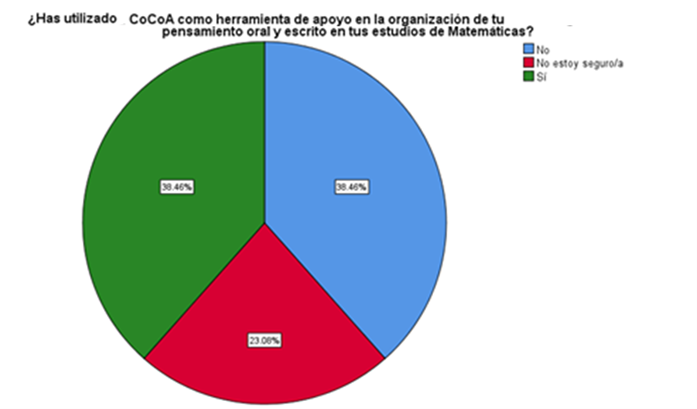
Figura 2
Uso del Sistema Computacional CoCoA
Los resultados de la encuesta indican que la mayoría de los estudiantes están familiarizados con el sistema computacional CoCoA y su propósito en la comunicación. Específicamente, el 61,54 % de los encuestados respondieron afirmativamente como se muestra en la figura 1.
Asimismo, el 38,46 % del estudiantado confirmaron haber utilizado CoCoA como herramienta de apoyo en la organización de su pensamiento oral y escrito en sus estudios de matemáticas, lo que sugiere tasa media de adopción de la herramienta entre los participantes.
Balladares Burgos et al. (2016) resaltan que el pensamiento computacional es un concepto complejo que implica habilidades abstractas, matemáticas, pragmáticas e ingenieriles. Para promoverlo, no basta con el mero conocimiento de las herramientas tecnológicas, sino que se requiere capacitar al profesorado en enfoques pedagógicos que permitan integrar las TIC de manera transversal en los procesos de enseñanza-aprendizaje. Así, para aprovechar el potencial de herramientas como CoCoA, las instituciones educativas deben hacer uso de ellas y adoptar un enfoque integral que desarrolle competencias en los estudiantes de forma significativa.
Se puede afirmar que, aunque una parte significativa de los estudiantes está familiarizada con CoCoA y algunos la utilizan para mejorar su pensamiento en matemáticas, es fundamental que se fortalezcan las estrategias pedagógicas y la formación docente. De esta manera, se garantiza que los estudiantes no solo conozcan y usen estas herramientas, sino que también desarrollen habilidades profundas y duraderas en el pensamiento computacional, lo que redundará en una mejor preparación académica y profesional en un entorno cada vez más orientado hacia la tecnología.
Por su parte, los docentes al preguntarles si han utilizado alguna vez el sistema computacional CoCoA como herramienta de apoyo en la enseñanza de Matemáticas, algunos contestaron (Profesores 1-8, comunicación personal 15 mayo, 2024):
Profesor 3: No lo he aplicado, Consideraría explorar su uso en el futuro para seguir mejorando la experiencia de aprendizaje de mis alumnos.
Profesor 6: No, claro que sí como parte de la formación continua necesaria en nuestro quehacer.
Profesor 7: Lo he utilizado, un par de veces, cuando estaba en la universidad, pero la poca práctica de este hace que no se recuerde, funciones ni comandos para el desarrollo de habilidades orales y escritas.
Se aprecia que los docentes, aunque facilitan componentes de Álgebra y relacionados a computación, desconocen del programa CoCoA como herramienta de apoyo en la enseñanza de Matemáticas. Aunque algunos muestran interés en explorar su uso en el futuro para mejorar la experiencia de aprendizaje de sus alumnos, otros reconocen la importancia de la formación continua en su quehacer docente pero no lo han aplicado en su práctica. Esto coincide con los resultados del estudio de Marín Romero & Rojas Martínez (2023), donde encontraron que la mayoría de los docentes, aunque imparten asignaturas donde se pueden utilizar herramientas tecnológicas, no lo hacen debido a la falta de capacitación y actualización continua, así como al interés limitado por parte del profesional en aprender nuevas tecnologías.
Tabla 3
Brecha tecnológica en la enseñanza de Matemáticas
| Disparidad entre estudiantes y docentes | Razones del Poco uso de CoCoA | Impacto Potencial de CoCoA en educación | Oportunidades y Desafíos |
|---|---|---|---|
| Existe una notable discrepancia entre la familiaridad de los estudiantes con CoCoA y su uso por parte de los docentes en la enseñanza de Matemáticas. Esto sugiere que los docentes no aprovechan estos recursos para mejorar significativamente la enseñanza y el aprendizaje de las matemáticas. | Según el estudio de Marín Romero & Rojas Martínez (2023), la falta de capacitación y actualización continua, así como el limitado interés por aprender nuevas tecnologías, son factores críticos que contribuyen al bajo uso de herramientas tecnológicas como ocurre con CoCoA por parte de los maestros. Esto indica una brecha en la formación docente que podría ser abordada con programas de desarrollo profesional específicos en el uso de herramientas tecnológicas en la enseñanza de las matemáticas. | Aunque no se ha implementado ampliamente entre los docentes, el uso de CoCoA entre los estudiantes tiene un potencial significativo para mejorar la sistematización del pensamiento matemático. Esto podría tener un impacto positivo en la comprensión y la resolución de problemas matemáticos, así como en el desarrollo de habilidades analíticas críticas. | La discrepancia entre el conocimiento de los estudiantes y el uso por parte de los docentes presenta tanto oportunidades como desafíos. Por un lado, existe una oportunidad para mejorar la educación matemática integrando herramientas computacionales avanzadas. Por otro lado, la capacitación docente y el cambio en la cultura educativa son desafíos importantes que deben abordarse para maximizar estas oportunidades. |
Eficacia del sistema computacional CoCoA
En el ámbito computacional, la eficacia se evalúa principalmente por la capacidad del sistema para resolver problemas de manera eficiente y concisa (Herrera-Castrillo, 2024; Herrera Herrera & Cisneros Díaz, 2022). CoCoA, en este contexto, se destaca como un sistema computacional especializado en álgebra, comparado frecuentemente con otros sistemas como Mathematica, Maple o SageMath en función de diversos criterios (Solórzano Rojas et al., 2015; Duque et al., 2002).
El rendimiento de CoCoA es notablemente competitivo en cálculos específicos de álgebra conmutativa y resolución de sistemas de ecuaciones polinomiales, donde demuestra una alta eficiencia. No obstante, sistemas de propósito más general como Mathematica y Maple ofrecen una mayor versatilidad para aplicaciones que se extienden más allá de este enfoque específico (Mantilla & Olaya-León, 2022; Stein, 2011).
La satisfacción del usuario es otra medida de eficacia en estos sistemas. En este sentido, CoCoA es apreciado por su facilidad de uso y enfoque especializado en cálculos algebraicos concretos, coincidiendo con las aplicaciones realizadas por Solórzano Rojas et al. (2015) fue diseñado para hacer frente a los problemas de la teoría de números y especialmente de polinomios.
La confiabilidad y disponibilidad de CoCoA lo convierten en un sistema altamente estable, especialmente adecuado para cálculos algebraicos especializados. En comparación, SageMath, como indican Pulido Rodríguez & López Bautista (2022) este integra múltiples bibliotecas, que pueden presentar retos de estabilidad debido a su mayor complejidad y dependencia de varios componentes, lo que a veces afecta su confiabilidad.
Otro aspecto clave es la eficiencia en el uso de memoria y CPU, CoCoA, al estar orientado a un ámbito específico, muestra un aprovechamiento optimizado de los recursos, lo que lo hace atractivo para tareas algebraicas enfocadas. En cambio, Mathematica y Maple, al ser sistemas de propósito más amplio, tienden a requerir mayor capacidad de memoria y procesamiento (Mantilla & Olaya-León, 2022; Pulido Rodriguez & López Bautista, 2022).
Desde el punto de vista del diseño, CoCoA tiene una estructura modular que facilita su integración en proyectos algebraicos específicos (Solórzano Rojas et al., 2015). Aunque Mathematica y SageMath también permiten una integración avanzada en áreas más amplias de matemáticas aplicadas, esto a menudo se traduce en un diseño más complejo. Por lo tanto, CoCoA se presenta como una solución sencilla y efectiva para quienes necesitan un sistema orientado a álgebra.
Finalmente, en términos de vida útil y criticidad, CoCoA mantiene su valor en el ámbito académico e investigativo, especialmente en contextos que requieren precisión en cálculos polinomiales. Si bien Mathematica y Maple son más críticos en aplicaciones industriales e ingenieriles, CoCoA sigue siendo una herramienta clave en el nicho de álgebra computacional, proyectándose como un sistema de relevancia y duración en este campo especializado.
Figura 3
Eficacia percibida del sistema computacional CoCoA para la organización del pensamiento oral
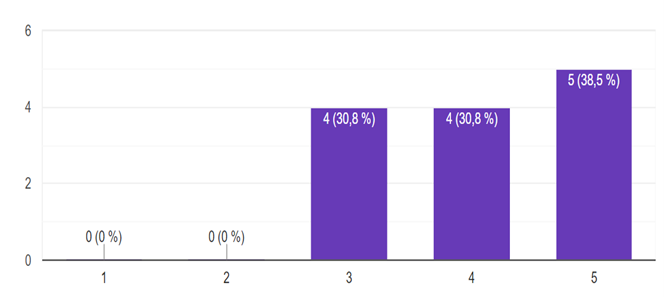
Según la figura 2, la percepción de los encuestados sobre la eficacia de CoCoA para la organización del pensamiento oral en estudios de Matemáticas es positiva. La mayoría de las respuestas se concentran en los niveles más altos de la escala, con un 38,5 % calificando la eficacia como “altamente eficaz” (nivel 5) y un 30,8 % considerándola como nivel 4. No se registraron respuestas en los niveles más bajos de “ineficaz” o apenas eficaz, lo que sugiere que esta herramienta es percibida como una ayuda valiosa en el contexto de los estudios de Matemáticas.
Herrera-Castrillo (2024) y Bernal et al. (2024) coinciden en que los diferentes sistemas de categorías y computacionales son eficaces en la organización del pensamiento al tener diversas aplicaciones prácticas en actividades científicas y tecnológicas dentro del Álgebra. Además, señalan que el pensamiento computacional se ha convertido en un componente crucial en el mercado laboral del futuro, con roles emergentes en áreas como la programación, el desarrollo de aplicaciones, la robótica y la domótica (conjunto de tecnologías que permiten controlar y automatizar la vivienda de manera inteligente).
Esto indica, que el uso de herramientas como CoCoA no solo facilita la comprensión y organización del pensamiento matemático en el presente, sino que también prepara a los estudiantes para enfrentar los desafíos tecnológicos del futuro. La formación en pensamiento computacional se perfila como fundamental no solo en el ámbito académico, sino también en el entorno profesional, donde la capacidad de resolver problemas complejos y adaptarse a nuevos entornos tecnológicos es cada vez más valorada.
Figura 4
Eficacia percibida del sistema computacional CoCoA para la organización del pensamiento escrito
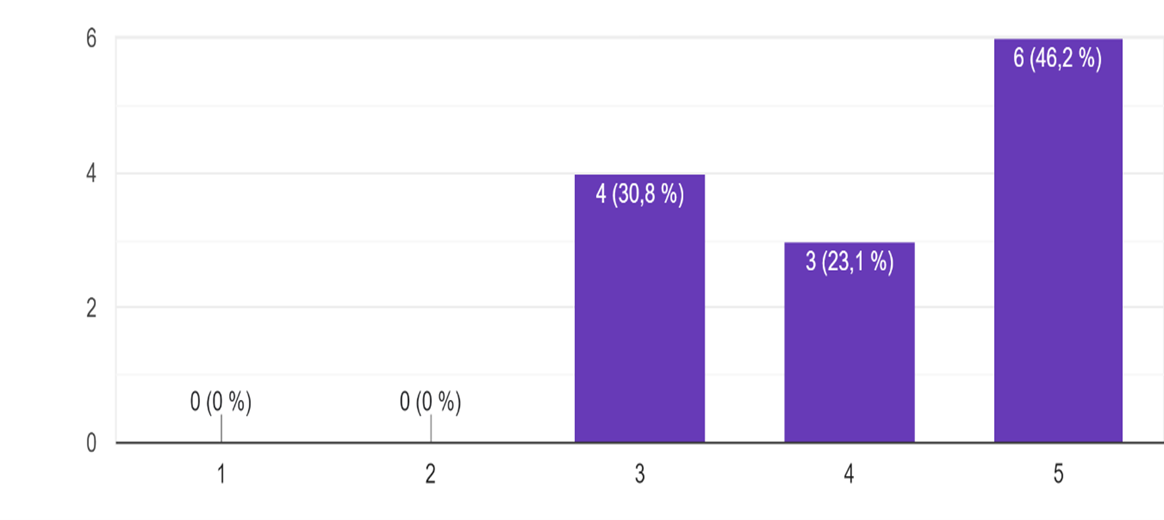
Los resultados indican que el uso de CoCoA es percibido como altamente eficaz para la organización del pensamiento matemático entre los encuestados. Casi la mitad de ellos (46,2 %) otorgaron la máxima puntuación de eficacia a esta herramienta, mientras que un tercio adicional (30,8 %) la valoraron con una puntuación de 4 sobre 5.
Estos datos sugieren que la integración de herramientas como CoCoA no solo beneficia la comprensión y estructuración del pensamiento matemático en el presente, sino que también prepara a los estudiantes para afrontar los desafíos tecnológicos del futuro (Herrera Herrera & Cisneros Díaz, 2022; Duque et al., 2002). La capacidad de resolver problemas complejos y adaptarse a nuevos entornos digitales, habilidades desarrolladas a través del pensamiento computacional, son cada vez más valoradas en el ámbito académico y profesional.
Por lo tanto, como indica Galeano Caicedo (2024) el uso de lenguajes de programación en la educación matemática tiene un impacto significativo y duradero, fortaleciendo las competencias clave necesarias en la era digital. Esta integración permite a los estudiantes desarrollar habilidades esenciales para enfrentar los desafíos del mundo actual, en el que la tecnología y la innovación juegan un papel fundamental en diversos ámbitos.
Al desarrollar habilidades de pensamiento computacional a través del uso de lenguajes de programación, los estudiantes no solo mejoran su capacidad de resolver problemas complejos, sino que también aprenden a organizar y secuenciar sus ideas de manera lógica. Estas competencias son fundamentales tanto para la expresión oral como para la redacción de textos académicos, informes y trabajos.
Del mismo modo que CoCoA ayuda a los estudiantes a comprender y ordenar sus razonamientos matemáticos, herramientas similares podrían potenciar la organización y fluidez del pensamiento escrito. Para Fernández Cabrera (2023) la práctica de plasmar ideas de forma estructurada y coherente en un programa o código podría transferirse a la habilidad de redactar textos bien argumentados y con una progresión temática clara.
Utilidad del sistema Computacional CoCoA
CoCoA es un sistema de álgebra computacional diseñado específicamente para trabajar con problemas de álgebra conmutativa y geometría algebraica (Solórzano Rojas et al., 2015). Esto lo convierte en un recurso invaluable para investigadores, matemáticos y científicos que trabajan en áreas como teoría de números, criptografía, bioinformática y optimización.
Además, CoCoA permite a los usuarios realizar cálculos complejos, generar modelos matemáticos, analizar datos y resolver problemas de manera eficiente y precisa. Su interfaz intuitiva y amplia biblioteca de funciones lo hacen accesible incluso para aquellos sin profundos conocimientos de programación.
Al preguntar a los estudiantes de Matemáticas sobre aspectos específicos, se ha encontrado que CoCoA resulta muy útil para la organización de su pensamiento, tanto oral como escrito, a lo largo de su carrera. El uso de esta herramienta les permite estructurar sus ideas de una manera clara y concisa, facilitando la comunicación de conceptos matemáticos complejos.
Figura 5
Uso del sistema computacional CoCoA
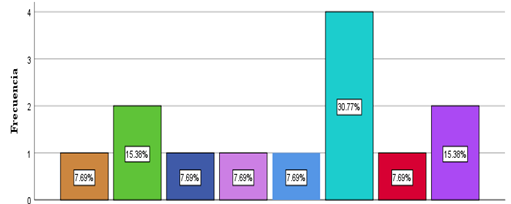
El gráfico muestra los diferentes aspectos específicos que se han encontrado útiles en CoCoA para la organización del procesamiento del lenguaje natural y escrito en la carrera de Matemáticas. En primer lugar, se destaca que el aspecto más utilizado es la “Identificación de puntos clave y argumentos principales”, con un 30.77 % de frecuencia. Esto indica que el sistema computacional algebraico ha sido especialmente útil para identificar los puntos clave y los argumentos principales en los textos analizados.
Otros aspectos relevantes son la “Generación de estructuras lógicas” (15.38 %), la “Generación de estructuras lógicas, Identificación de puntos clave y argumentos principales” (7.69 %), y la “Mejora de la coherencia y claridad de los textos” (7.69 %). Estos resultados sugieren que CoCoA también ha sido valioso para generar estructuras lógicas en los textos, así como para mejorar la coherencia y claridad de estos. En contraste, aspectos como “No lo he utilizado” (15.38 %) y “Sugerencias de vocabulario y corrección gramatical” (7.69 %) muestran que no todos los usuarios han encontrado estas funcionalidades igualmente útiles.
Como indica Solórzano Rojas et al. (2015) CoCoA ha sido valioso en varias áreas clave del procesamiento del lenguaje natural y escrito en la carrera de Matemáticas, como la identificación de puntos clave, la generación de estructuras lógicas y la mejora de la coherencia y claridad de los textos. Sin embargo, también indica que hay funciones menos utilizadas, como las correcciones gramaticales y las sugerencias de vocabulario, y que una proporción de usuarios no ha aprovechado la herramienta.
Es importante, contrastar estos resultados con los recursos o herramientas utiliza por los docentes para apoyar el aprendizaje de los estudiantes en Matemáticas, donde se destaca:
Figura 6
Nube de palabras sobre recursos que utilizan los docentes

La utilización de tecnología como Google Forms y GeoGebra, así como aplicaciones móviles y plataformas digitales, complementan a CoCoA, pese a que los maestros no lo conocen. Estas herramientas facilitan la “Identificación de puntos clave y argumentos principales” en textos matemáticos al permitir análisis detallados y visuales de conceptos complejos (Fonseca Gómez, 2023; Motoa, 2019).
Los “Manipulativos físicos” como bloques y ábacos también son utilizados para enseñar conceptos matemáticos de manera práctica y visual, complementando el uso de tecnología digital. La “Gamificación” y los “Juegos educativos” son métodos que no solo fomentan el pensamiento crítico y la resolución de problemas, sino que también mejoran la coherencia y claridad de los textos al presentar los contenidos de manera más atractiva y comprensible para los estudiantes (González-Fernández et al., 2021).
Al preguntar a los docentes, ¿Qué beneficios considera que podría ofrecer CoCoA en el aprendizaje y enseñanza de Matemáticas? Algunos indicaron (Profesores 1-8, comunicación personal 15 mayo, 2024):
Profesor 1: No lo he aplicado y tampoco he interactuado, pero considero ayuda a facilitar el acceso a herramientas de cálculo avanzado para resolver problemas matemáticos de manera más eficiente y precisa. También, ayuda a fomentar el desarrollo de habilidades de programación y algoritmos, brindando a los estudiantes una mayor comprensión del pensamiento computacional en el contexto matemático.
Profesor 4: Comprender una matemática más generalizados y desarrollo de los alumnos en sus aprendizajes, pensamiento crítico.
Profesor 8: Una mejor compresión del lenguaje matemático y el desarrollo de habilidades tecnológicas.
Los docentes coinciden en que el uso de CoCoA podría mejorar significativamente el aprendizaje de las matemáticas en los estudiantes. La herramienta ofrece acceso a funciones avanzadas que no solo facilitan la resolución de problemas matemáticos complejos, sino que también fomentan el desarrollo de habilidades en programación y algoritmos. Esta combinación de capacidades no solo enriquece el conocimiento técnico, sino que también promueve una comprensión más profunda del lenguaje matemático y del pensamiento computacional.
Como señala Adell Segura et al. (2019), la integración de CoCoA en el currículo educativo proporciona una plataforma para que los estudiantes desarrollen una comprensión más robusta y aplicada de los conceptos matemáticos. Esto se debe a que la herramienta permite la implementación práctica de teorías matemáticas a través de la programación, lo que facilita la visualización de las relaciones entre diferentes conceptos matemáticos y su aplicación en contextos reales.
Un aspecto interesante de la combinación de recursos y herramientas utilizadas en el Álgebra Conmutativa, dado que permite brindar un enfoque integral que apoye el aprendizaje de los estudiantes en matemáticas. Esta integración puede mejorar significativamente la comprensión y el procesamiento de habilidades orales y escritas en esta disciplina.
CoCoA ofrece diversas capacidades que pueden ser valiosas para el aprendizaje de las matemáticas. Primero, el procesamiento del lenguaje natural permite analizar y comprender el lenguaje matemático utilizado en los problemas y enunciados. Esto puede facilitar la interpretación y la traducción de conceptos abstractos a un lenguaje más accesible para los estudiantes.
Además, las herramientas de manipulación simbólica dentro de CoCoA permiten realizar operaciones algebraicas, cálculo de derivadas, integrales y otras tareas de manera automatizada. Como indica Fernández Cabrera (2023) esto permite aliviar la carga cognitiva de los estudiantes y permitirles enfocarse en la comprensión conceptual, en lugar de dedicar tiempo a procedimientos mecánicos, esto si debe saberse aplicar correctamente por parte del docente, quien es el guía del proceso.
Asimismo, para Solórzano Rojas et al. (2015) y Duque et al. (2002) la interactividad que brinda CoCoA permite que los estudiantes prueben diferentes enfoques, reciban retroalimentación inmediata y exploren los conceptos de manera más activa. Esto puede fomentar un aprendizaje más profundo y significativo, en lugar de un enfoque puramente memorístico.
Al integrar estas diversas capacidades, CoCoA ofrece un entorno de aprendizaje robusto y personalizado, donde los estudiantes puedan desarrollar una mejor comprensión y dominio del lenguaje matemático. Sin embargo, es importante considerar cómo implementar estas herramientas de manera efectiva en los planes de estudio y actividades de aula, asegurando que complementen y apoyen los métodos de enseñanza tradicionales.
Organización del Pensamiento en estudiantes de Matemáticas
La organización del pensamiento es un aspecto fundamental en el correcto uso de sistemas computacionales. Estos permiten estructurar y expresar sus ideas de una manera clara y lógica. Dando una definición de elementos como variables, funciones, clases y estructuras de datos que reflejen la forma en que el ser humano concibe y manipula la información.
Una buena organización del pensamiento en el código facilita la lectura, mantenimiento y escalabilidad de los programas, permitiendo que estos se adapten a las necesidades cambiantes de los usuarios y del negocio. Por lo tanto, los diseñadores de lenguajes de programación, utilizados en los sistemas computacionales deben prestar especial atención a cómo el pensamiento humano se traduce en construcciones sintácticas y semánticas que optimicen la expresión de soluciones computacionales.
Al preguntar a los estudiantes y docentes sobre: ¿Recomendaría el uso de CoCoA a estudiantes o docentes de Matemáticas para mejorar su organización del pensamiento oral y escrito? Se obtuvo (Profesores 1-8, comunicación personal 15 mayo, 2024) y (Profesores 1-13, comunicación Estudiante 15 mayo, 2024):
Estudiante 6: Si es muy importante para mejorar nuestro pensamiento oral y escrito y así aprender cada día más.
Estudiante 11: Si porque se hace más fácil resolver ejercicios.
Estudiante 12: Si porque desde el punto de vista es bien práctico.
Profesor 2: Si la recomendaría, tanto a estudiantes, como a docentes, para que realicen de una forma más eficiente ejercicios de álgebra conmutativa, eso sí aún existe el desafío de estar a la par de los estudiantes en el uso de tecnología.
Profesor 4: Si, ya que hoy en día se tiene que estar actualizado con la tecnología, además como matemáticos el desarrollo del pensamiento lógico, computacional y algorítmico son de gran importancia.
Profesor 8: Si, para seguir aprendiendo.
Los estudiantes destacan la importancia para el desarrollo de habilidades tanto orales como escritas, subrayando su practicidad y facilidad en la resolución de ejercicios. Esta perspectiva indica que los estudiantes encuentran en CoCoA una herramienta que facilita su proceso de aprendizaje y contribuye a su formación diaria.
Por su parte, los docentes enfatizan la eficiencia que proporciona CoCoA en la realización de ejercicios de álgebra conmutativa y resaltan la necesidad de estar al día con las tecnologías emergentes. Además, se reconoce el valor del pensamiento lógico, computacional y algorítmico en el campo de la matemática. A pesar de las ventajas mencionadas, los profesores también señalan el desafío de mantenerse actualizados con el uso de nuevas tecnologías al mismo nivel que los estudiantes.
Es importante considerar ciertas limitaciones del estudio. La muestra, aunque representativa, es limitada en tamaño, lo que podría afectar la generalización de los hallazgos. Además, la implementación de CoCoA en el currículo requiere una formación adecuada de los docentes, lo cual puede ser un desafío en algunos contextos educativos.
Este estudio, en consonancia con los hallazgos de Balladares Burgos et al. (2016), subraya la necesidad de una alfabetización digital integral del profesorado. Solo así se podrá asegurar que las TIC no solo sean utilizadas, sino que promuevan un aprendizaje significativo. La integración de herramientas digitales como CoCoA debe ser vista como una parte esencial del currículo educativo, fomentando un pensamiento computacional que atraviese diversas disciplinas y contextos.
No obstante, los resultados sugieren que CoCoA tiene el potencial de transformar la manera en que los estudiantes de matemáticas organizan y comunican sus ideas. Para maximizar su impacto, es crucial que las instituciones educativas inviertan en la capacitación de docentes y en la integración de estas herramientas en el currículo de manera efectiva.
CONCLUSIONES
El estudio revela que CoCoA ha demostrado ser una herramienta altamente eficaz para la organización del pensamiento oral y escrito en estudiantes de matemáticas. Los resultados indican que facilita la identificación de puntos clave, la generación de estructuras lógicas claras y mejora significativamente la coherencia y claridad en la expresión de ideas matemáticas complejas. Este impacto positivo sugiere que CoCoA no solo promueve una comprensión más profunda de los conceptos, sino que también fortalece las habilidades de comunicación matemática entre los estudiantes.
Además, la integración de CoCoA en el currículo educativo no solo beneficia el aprendizaje actual, sino que también prepara a los estudiantes para enfrentar los desafíos tecnológicos del futuro. Al fomentar el desarrollo del pensamiento computacional y algorítmico, esta herramienta no solo mejora la resolución de problemas matemáticos, sino que también cultiva habilidades esenciales para roles emergentes en áreas como la programación y la tecnología aplicada. Esto subraya la importancia de CoCoA como una preparación integral para el mercado laboral moderno, donde la habilidad de adaptarse a entornos tecnológicos complejos es crucial.
El artículo también revela una disparidad notable entre el conocimiento y la utilización de CoCoA entre estudiantes y docentes de matemáticas. Mientras que la mayoría de los estudiantes expresan familiaridad con CoCoA y destacan su utilidad, muchos docentes admiten no estar tan familiarizados con esta herramienta. Esta brecha subraya la necesidad urgente de programas de formación para los docentes, destinados a cerrar esta brecha digital y aprovechar plenamente el potencial educativo de CoCoA en el aula. Además, resalta la importancia de integrar nuevas tecnologías de manera efectiva en el currículo educativo para garantizar una preparación adecuada de los estudiantes.
Con base en las percepciones positivas de estudiantes y docentes, se recomienda ampliar y fortalecer la integración de CoCoA en los planes de estudio de matemáticas. Es crucial que las instituciones educativas proporcionen formación continua a los docentes para garantizar un uso efectivo de esta herramienta. Además, se sugiere la realización de estudios longitudinales para evaluar el impacto a largo plazo de CoCoA, así como explorar su aplicación en otras disciplinas académicas.
Se sugiere implementar programas de formación continua para docentes, a fin de asegurar que puedan utilizar CoCoA de manera efectiva en sus prácticas educativas. La colaboración entre instituciones educativas y desarrolladores de software también podría ser beneficiosa para adaptar CoCoA a las necesidades específicas de los estudiantes y docentes. Se recomienda realizar estudios longitudinales para evaluar el impacto a largo plazo de CoCoA y explorar su aplicación en otras disciplinas académicas.
Estas conclusiones reflejan el valor significativo de CoCoA como una herramienta educativa que no solo mejora la comprensión y organización del pensamiento matemático, sino que también prepara a los estudiantes para los desafíos tecnológicos y profesionales del siglo XXI.
REFERENCIAS BIBLIOGRÁFICAS
Adell Segura, J., Llopis Nebot, M. A., Esteve Mon, F. M., & Valdeolivas Novella, M. G. (2019). El debate sobre el pensamiento computacional en educación. Revista Iberoamericana de Educación a Distancia, 22(1), 171-186. https://doi.org/10.5944/ried.22.1.22303
Balladares Burgos, J. A., Avilés Salvador, M. R., & Pérez Narváez, H. O. (2016). Del pensamiento complejo al pensamiento computacional retos para la educación contemporánea. Sophia: Colección de Filosofía de la Educación(21), 143-159. https://doi.org/10.17163/soph.n21.2016.06
Bernal Párraga, A. P., Baquez Chávez, A. L., Hidalgo Jaen, N. G., Mera Alay, N. A., & Velásquez Araujo, A. L. (2024). Pensamiento Computacional: Habilidad Primordial para la Nueva Era. Ciencia Latina Revista Científica Multidisciplinar, 8(2), 5177-5195. https://doi.org/10.37811/cl_rcm.v8i2.10937
Casado-Mancebo, M. (2022). Una aproximación a la lingüística computacional. Sincronía Revista de Filosofía, Letras y Humanidades, 26(81), 746-761. https://doi.org/10.32870/sincronia.axxvi.n81.34a22
Condori-Ojeda, P. (2020). Universo, población y muestra. Curso Taller. https://www.aacademica.org/cporfirio/18.pdf
Duque, Á., Rodríguez, P., & Novoa, F. (2002). Un programa para calcular las representaciones irreducibles de Sn en la forma seminormal de Young, matemática computacional como apoyo a la docencia. Universitas Scientiarum, 7(1), 5-16. https://www.redalyc.org/pdf/499/49925477003.pdf
Fernández Cabrera, J. V. (2023). Explorando las matemáticas: un recorrido por su fascinante mundo. Programación didáctica de matemáticas 4º ESO. [Tesis de Maestría]. Universidad Europea Canarias. https://titula.universidadeuropea.com/handle/20.500.12880/6399
Fonseca Gómez, L. (2023). Las inferencias como estrategia para el fortalecimiento de la argumentación oral. [Tesis de Grado]. Universidad Pedagógica Nacional de Colombia | Facultad de Humanidades, Bogota, Colombia. http://repository.pedagogica.edu.co/handle/20.500.12209/18504
Galeano Caicedo, J. A. (2024). Análisis de competencias lógico-matemáticas para la creación de rutas de aprendizaje en la Universidad de los Andes. [Tesis de Grado]. Universidad de los Andes. https://repositorio.uniandes.edu.co/entities/publication/65bef9ea-b9f9-41e8-8c77-00e91027d345
González-Fernández, M. O., González-Flores, Y. A., & Muñoz-López, C. (2021). Panorama de la robótica educativa a favor del aprendizaje STEAM. Revista Eureka sobre Enseñanza y Divulgación de las Ciencias (REurEDC), 18(2), 1-19. https://doi.org/10.25267/Rev_Eureka_ensen_divulg_cienc.2021.v18.i2.2301
Hernández González, O. (2021). Aproximación a los distintos tipos de muestreo no probabilístico que existen. Revista Cubana de Medicina General Integral, 37(3), 1-3. http://scielo.sld.cu/scielo.php?pid=S0864-21252021000300002&script=sci_arttext
Herrera Herrera, A. A., & Cisneros Díaz, I. A. (2022). Algoritmización para la resolución de ecuaciones no lineales mediante la técnica de iteración variacional. Revista Científica Estelí: medio ambiente, tecnología y desarrollo humano(41), 60-76. https://doi.org/10.5377/farem.v11i41.13886
Herrera-Castrillo, C. J. (2024). Aplicaciones del Lenguaje de Categorías en diferentes actividades científicas y tecnológicas. Ciencia e Interculturalidad, 33(2), 187-204. https://doi.org/10.5377/rci.v33i2.17723
Itcara Palacios, S. P. (2014). Manual de investigación cualitativa. Fontamara. https://repositorio.minedu.gob.pe/handle/20.500.12799/4613
Manterola, C., Hernández-Leal, M. J., Otzen, T., Espinosa, M. E., & Grande, L. (2023). Estudios de Corte Transversal. Un Diseño de Investigación a Considerar en Ciencias Morfológicas. International Journal of Morphology, 41(1), 146-155. http://dx.doi.org/10.4067/S0717-95022023000100146
Mantilla, R. J., & Olaya-León, W. (2022). Sobre composiciones de enteros usando SageMath. Ciencia en Desarrollo, 13(2), 85-97. https://doi.org/10.19053/01217488.v13.n2.2022.13914
Marín Romero, D. Y., & Rojas Martínez, A. I. (2023). Tecnología Educativa para el Desarrollo del Pensamiento Computacional. [Tesis de Maestría]. Universidad de Santander. https://repositorio.udes.edu.co/server/api/core/bitstreams/9b276061-d16d-441f-abc6-cf37ea724218/content
Medina-Hernández, E. J., Muñiz, J. L., Guzmán-Aguiar, D. S., & Holguín-Higuita, A. (2022). Recursos y estrategias para la enseñanza de la estadística y la analítica de datos en la educación superior. Formación universitaria, 15(3), 61-68. https://www.scielo.cl/scielo.php?pid=S0718-50062022000300061&script=sci_arttext
Méndez López, D. A., & Cisneros Díaz, I. A. (2022). Algoritmos de Ecuaciones no Lineales por Polinomios de Adomian. Revista Científica Estelí: medio ambiente, tecnología y desarrollo humano(42), 68–82. https://doi.org/10.5377/farem.v11i42.14688
Mendoza Arenas, R. D., Amaru Castillo Paredes, O. T., Meza Ramos, M. R., Estrella Serón, G. I., Falcón Cerna, A. N., & La Chira Loli , M. B. (2023). Inteligencia digital y el desarrollo del pensamiento computacional: Una vertiente de los cursos masivos abiertos. Editorial Mar Caribe de Josefrank Pernalete Lugo. https://repositorio.unac.edu.pe/handle/20.500.12952/8027
Motoa, S. P. (2019). Pensamiento Computacional. Revista Educación y Pensamiento, 26(26), 107-111. http://educacionypensamiento.colegiohispano.edu.co/index.php/revistaeyp/article/view/104
Palacios Almendros, P. (2023). Métodos algebraicos para el análisis de circuitos aritméticos en pruebas de conocimiento nulo. [Tesis de Grado]. Universidad Complutense de Madrid. https://docta.ucm.es/rest/api/core/item/ab713d5b-6ecf-4a83-80b5-6e4b4c8c3e9c/export/zotero
Pantoja-Oñate, M. J. (2022). Fortalecimiento de Habilidades de Pensamiento Computacional con la Metodología Steam a Través de la Plataforma Edmodo Para Desarrollar Competencias de Ciencias Naturales en Estudiantes de Séptimo. [Tesis de Maestría]. Universidad de Santander. https://repositorio.udes.edu.co/entities/publication/ad1b8fa9-71c8-4796-a583-d485b7f217d8
Posso Domínguez, M. E., & Murcia Londoño, E. (2023). Las “actividades desconectadas” y el desarrollo del pensamiento algorítmico. Universidad Católica de Pereira, 1(2), 1-35. https://repositorio.ucp.edu.co/entities/publication/83a10485-1365-4c57-b959-926a9ebea946
Pulido Rodríguez, G., & López Bautista, R. (2022). Integración de herramientas en Moodle con aplicaciones a cursos de Matemáticas para ingenieros. Avances de las MUJERES en las CIENCIAS las humanidades y todas las disciplinas | VI Congreso Internacional Medio Ambiente, Riesgo, Vulnerabilidad y Cambio Climático, 13(2), 93-103. https://acortar.link/Ozmf8Y
Restrepo Pineda, A. F. (2024). Conectando mentes y máquinas: neuroeducación e IA en la era del pensamiento computacional. Plumilla Educativa, 1(33), 1-15. https://doi.org/10.30554/p.e.1.5090.2024
Sánchez Martínez, D. V. (2022). Técnicas e instrumentos de recolección de datos en investigación. TEPEXI Boletín Científico de la Escuela Superior Tepeji del Río, 9(17), 38-39. https://doi.org/10.29057/estr.v9i17.7928
Sánchez, M. Z., Mejías, M., & Olivety, M. (2022). Diseño de Metodologías Mixtas una revisión de las estrategias para combinar. Revista Electrónica Human@s Enfermería en Red, 3, 10-13. https://www.portal.uasj.unpa.edu.ar/_files/ugd/f9834d_784cc19611714c87890006bc7cb4715d.pdf#page=10
Sánchez-Camacho, R., & Grane, M. (2023). Programas de Pensamiento Computacional en educación primaria: una revisión sistemática. Digital Education Review(44), 133-145. https://doi.org/10.1344/der.2023.44.133-145
Solórzano Rojas, K. D., Lanzas Arechavala, Y. R., & Ramírez Bonilla, Y. A. (2015). Resolución de Sistemas de Ecuaciones Polinomiales utilizando las Bases de Gröbner y el Método de Autovalores. [Tesis de grado]. UNAN-Managua. https://repositorio.unan.edu.ni/1251/
Stein, W. (2011). Sage: creating a viable free open Source alternative to Magma, Maple, Mathematica, and MATLAB [Sage: creación de una alternativa viable de código abierto y gratuito a Magma, Maple, Mathematica y MATLAB]. Foundations of Computational mathematics, Budapest(403), 230-238. https://wstein.org/grants/2012-appengine/proposal.pdf
Tamayo, C., & Silva, I. (2012). Técnicas e Instrumentos de Recolección de Datos. https://n9.cl/jbmcp
Triminio-Zavala, C. M., Herrera-Castrillo, C. J., & Medina-Martínez, W. I. (2024). Formación investigativa del estudiante universitario en el Modelo por competencia de UNAN-Managua. Revista Científica Estelí: medio ambiente, tecnología y desarrollo humano, 12(48), 108–128. https://doi.org/10.5377/farem.v12i48.17529
Valero Avilés, M. V. (2022). Estudio comparativo de las aplicaciones móviles híbridas desarrolladas con el lenguaje de programación JavaScript, y las aplicaciones móviles nativas. [Tesis de grado]. Universidad Técnica de Babahoyo. https://dspace.utb.edu.ec/handle/49000/11862
Valle Taiman, A., Manrique Villavicencio, L., & Revilla Figueroa, D. (2022). La Investigación Descriptiva con Enfoque Cualitativo en Educación. Pontificia Universidad Católica del Perú. https://repositorio.pucp.edu.pe/index/handle/123456789/184559
Vásquez Acevedo, H. M., Licona Suarez, L. J., & Felizzola Medina, L. D. (2023). Pensamiento Computacional: una competencia del siglo XXI Revisión sistemática en Scopus. Revista Latinoamericana Ogmios, 4(9), 1-16. https://doi.org/10.53595/rlo.v4.i9.090
© 2024 Revista Científica Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
