Dificultades en la Enseñanza-Aprendizaje del Cálculo Diferencial en carreras de Ingeniería de UNAN-Managua, CUR-Estelí Nicaragua

Difficulties in Teaching and Learning Differential Calculus in Engineering Programs at UNAN-Managua, CUR-Estelí Nicaragua

 

José Ismael González
Universidad Nacional Autónoma de Nicaragua, Managua. Centro Universitario Regional de Estelí
https://orcid.org/0000-0001-5232-0266
joseismael26@yahoo.com

RECIBIDO

20/02/2025

ACEPTADO

02/07/2025

 

RESUMEN

El presente artículo analiza las dificultades del proceso de enseñanza-aprendizaje del Cálculo Diferencial en las carreras de ingeniería impartidas en la UNAN-Managua/CUR-Estelí, enfatizando los desafíos metodológicos y conceptuales que enfrentan docentes y estudiantes. Se empleó un muestreo no probabilístico intencional u opinático, para la elección de la muestra.  En el I semestre 2023 se realizó la revisión documental y entrevistas a docentes de matemática. Los resultados evidencian que la naturaleza abstracta del Cálculo Diferencial, sumada a la falta de estrategias didácticas adecuadas, dificulta su comprensión. Factores como la insuficiente integración de tecnologías en el aula, la resistencia al cambio metodológico y las limitaciones en el dominio de las TIC, tanto por parte de los docentes como de los estudiantes, agravan esta problemática. La investigación plantea la necesidad de incorporar herramientas digitales y enfoques pedagógicos innovadores para fortalecer la enseñanza del Cálculo Diferencial. La adopción de metodologías activas y recursos interactivos facilita la asimilación de conceptos fundamentales, también contribuye al desarrollo de competencias transversales esenciales en la formación de ingenieros. El estudio concluye que la transformación de las estrategias educativas es clave para optimizar el aprendizaje y preparar a los estudiantes para afrontar los retos de su ejercicio profesional.

 

PALABRAS CLAVE

Cálculo Diferencial; Ingeniería; TIC; aprendizaje; competencias.

 

ABSTRACT

This article analyzes the difficulties of the teaching-learning process of Differential Calculus in engineering courses taught at UNAN-Managua/CUR-Estelí, emphasizing the methodological and conceptual challenges faced by teachers and students. An intentional or opinion-based non-probabilistic sampling method was used to select the sample. In the first semester of 2023, a document review and interviews with mathematics teachers were conducted. The results show that the abstract nature of differential calculus, combined with the lack of adequate teaching strategies, makes it difficult to understand. Factors such as insufficient integration of technologies in the classroom, resistance to methodological change, and limitations in ICT proficiency, both on the part of teachers and students, exacerbate this problem. The research raises the need to incorporate digital tools and innovative pedagogical approaches to strengthen the teaching of differential calculus. The adoption of active methodologies and interactive resources facilitates the assimilation of fundamental concepts and also contributes to the development of cross-cutting skills that are essential in the training of engineers. The study concludes that the transformation of educational strategies is key to optimizing learning and preparing students to face the challenges of their professional practice.

 

KEYWORDS

Differential calculus; Engineering; ICT; learning; skills.

 

INTRODUCCIÓN

 

El Cálculo Diferencial es un pilar fundamental en la formación de ingenieros, ya que permite desarrollar competencias claves como el pensamiento crítico, el razonamiento lógico y la resolución de problemas aplicados en contextos reales (Estrada et al., 2022). Según Paulette (2023) es una de las ramas fundamentales de las matemáticas, para los estudiantes de ingeniería, ya que proporciona las herramientas matemáticas necesarias para modelar y analizar sistemas dinámicos. También Stewart (2008), afirma que el cálculo es esencial para modelar y predecir fenómenos físicos y mecánicos, ya que permite comprender cómo cambian los sistemas y prever su comportamiento ante diferentes condiciones.

De acuerdo con los autores antes señalados, la relevancia del Cálculo Diferencial radica en su capacidad para vincular conceptos abstractos con aplicaciones prácticas, facilitando no solo la comprensión teórica, sino también su adaptación a contextos reales. No obstante, su enseñanza y aprendizaje presentan múltiples dificultades, principalmente debido a la naturaleza abstracta de sus conceptos y la persistencia de metodologías tradicionales que limitan la apropiación significativa del conocimiento. En este contexto, la baja comprensión de conceptos esenciales como límite, continuidad y derivada impacta negativamente en el aprendizaje de los estudiantes y en su capacidad para aplicar estos conocimientos en situaciones prácticas.

Otros estudios afirman que la enseñanza del Cálculo Diferencial enfrenta barreras metodológicas significativas, entre ellas la escasa integración de recursos TIC y la falta de estrategias didácticas innovadoras (Olmedo y Farrerons, 2017). A pesar de los avances en enfoques pedagógicos, como el aprendizaje basado en la resolución de problemas propuesto por Polya (1957), la resistencia al cambio y la limitada formación continua de los docentes siguen siendo obstáculos para la mejora del proceso educativo.

En la enseñanza del Cálculo Diferencial, el uso sistemático de las TIC obliga a replantear las estrategias didácticas, dando mayor relevancia a métodos gráficos y numéricos. Este enfoque fomenta la motivación del estudiante, ayudándolo a descubrir sus capacidades y enfrentarse a nuevas situaciones de aprendizaje con mayor confianza (Pino y Salazar, 2018). Desde esta perspectiva, el docente debe asumir un papel protagonista y transformador, adaptando las estrategias tradicionales para integrar las tecnologías en el aula, lo que requiere una formación continua en competencias digitales (Revelo y Carrillo, 2018). Esta renovación metodológica no solo fortalece el proceso de enseñanza, sino que también potencia el desarrollo de competencias clave en el área de matemáticas.

La presente investigación se justifica en la necesidad de abordar las persistentes dificultades del proceso de enseñanza-aprendizaje del Cálculo Diferencial en las carreras de ingeniería de la UNAN-Managua/CUR-Estelí. Estos desafíos metodológicos y conceptuales impactan negativamente el rendimiento académico y la futura práctica profesional de los estudiantes. El estudio busca identificar y analizar dichos factores, como la insuficiente integración de TIC y la prevalencia de estrategias tradicionales, para proponer soluciones innovadoras. Contribuir a la mejora del proceso es vital para que los futuros ingenieros adquieran las habilidades necesarias y afronten los retos de una sociedad global y tecnológicamente avanzada.

En este contexto, se destaca la importancia del uso de metodologías activas e interactivas para favorecer un aprendizaje significativo y contextualizado. Desde una perspectiva práctica, la investigación contribuye a la identificación de estrategias que permitan optimizar la enseñanza del Cálculo Diferencial, promoviendo una mayor integración de las TIC y metodologías innovadoras que ofrecen una base para la reflexión y la implementación de mejoras en el proceso formativo de los futuros ingenieros.

Fundamentación teórica

Los principales conceptos que aborda este estudio son:

• Cálculo Diferencial: entendido como la rama de las matemáticas que estudia el cambio de las funciones y sus aplicaciones, siendo crucial para el modelado y análisis de sistemas dinámicos en ingeniería (Stewart, 2008 ; Paulette 2023).
• Educación en ingeniería: se refiere a los procesos formativos que buscan desarrollar en los estudiantes las competencias necesarias para el ejercicio profesional de la ingeniería, incluyendo pensamiento crítico, resolución de problemas y razonamiento lógico (Estrada et al., 2022).
• Tecnologías de la Información y Comunicación (TIC): herramientas y recursos digitales que pueden integrarse en el proceso educativo para mejorar la enseñanza y el aprendizaje, facilitando la visualización, interacción y acceso a la información (Pino y Salazar, 2018 ; Rojas, 2021).
• Aprendizaje: proceso mediante el cual los estudiantes adquieren conocimientos, habilidades y valores. El estudio se enfoca en el "aprendizaje significativo", donde el conocimiento se integra de manera no arbitraria con la estructura cognitiva del estudiante, en contraste con el aprendizaje memorístico (Medina y Salvador, 2009).
• Competencias: conjunto de conocimientos, habilidades, destrezas y valores que una persona posee y aplica para desempeñarse eficazmente en diversos contextos (López y Farfán, 1998). En el contexto universitario de la UNAN-Managua, se refieren tanto a competencias disciplinares (matemáticas) como transversales (resolución de problemas, comunicación, uso de TIC).
  

El objetivo del estudio fue analizar las dificultades en el proceso de enseñanza-aprendizaje del Cálculo Diferencial en las carreras de ingeniería, identificando los principales factores que afectan la formación de los estudiantes y proponiendo estrategias de mejora.

 

MATERIALES Y MÉTODOS

 

La investigación es de tipo descriptiva, y de acuerdo al enfoque filosófico es cualitativa, porque analiza a profundidad las dificultades en la enseñanza-aprendizaje del Cálculo Diferencial en las carreras de ingeniería. Se fundamentó en el enfoque constructivista, que sitúa al estudiante como agente activo en la construcción de su conocimiento (Piaget, citado por Olmedo y Farrerons, 2017). Asimismo, se destaca la importancia del uso de metodologías activas e interactivas para favorecer un aprendizaje significativo y contextualizado.
La población la conformaron 10 docentes de matemática de la UNAN-Managua/CUR-Estelí. El método de selección de la muestra fue el muestreo no probabilístico intencional u opinático, “en este caso los elementos son escogidos con base a criterios o juicios preestablecidos por el investigador” (Arias, 2012, p. 85). Los criterios de selección (o de inclusión) de la muestra son:

• Ser docente de aula en el área de matemática con experiencia de 5 años o más.
• Contar con la experiencia y conocimientos en el desarrollo de contenidos de Cálculo Diferencial.
• Ser docente en el área de matemática en UNAN Managua/CUR-Estelí.
• Accesibilidad y disposición para participar en la investigación.

Se tomó una muestra de 5 maestros de matemática conformada por 4 varones y 1 mujer. 

Las técnicas utilizadas fueron: revisión documental exhaustiva, analizando el Modelo Curricular de la UNAN-Managua, los programas, componentes, planes didácticos y bibliografía recomendada. Se aplicó entrevistas semiestructuradas a docentes especialistas en matemática para explorar las percepciones sobre las principales dificultades pedagógicas, las estrategias didácticas utilizadas y las oportunidades de mejora en el proceso educativo.

Etapas de la investigación

Etapa 1. Revisión documental

Inicialmente se realizó revisión de modelo por competencias de la UNAN-Managua, los componentes de matemática que contienen contenidos de Cálculo Diferencial, planificaciones didácticas y la bibliografía recomendada en los componentes. También se revisó literatura relacionada con la temática en estudio para consolidar los antecedentes y construir el sustento teórico.

Etapa 2. Trabajo de campo

En un segundo momento, se aplicaron entrevistas a los docentes seleccionados, uno a uno. Cada entrevista tuvo una duración aproximada de 45 a 60 minutos. El propósito fue obtener información detallada en relación con la enseñanza-aprendizaje del Cálculo Diferencial y la implementación de las TIC en sus prácticas docentes.

Se hizo énfasis sobre su experiencia en la enseñanza del Cálculo Diferencial, las dificultades observadas en los estudiantes, las estrategias didácticas que utilizan habitualmente, la integración de TIC en sus clases y evaluaciones, su percepción sobre la actualización de los programas y bibliografía, y las capacitaciones recibidas en herramientas digitales. Las entrevistas fueron grabadas (con consentimiento previo) y posteriormente transcritas lo que permitió capturar la riqueza de las perspectivas docentes y sus experiencias directas en el aula.

Etapa 3. Análisis de la información

La información obtenida de la revisión documental y las transcripciones de las entrevistas se analizó para considerar su incorporación en la propuesta didáctica. Los datos recopilados con las entrevistas se procesaron en el Software ATLAS.ti 24. La triangulación de la información entre la revisión documental y las entrevistas fortaleció la validez del estudio, proporcionando una visión integral del problema investigado y orientando las conclusiones hacia propuestas de mejora concretas en el ámbito educativo. Finalmente, se procedió a realizar las respectivas conclusiones en correspondencia con los hallazgos y el objetivo, y se efectuó la confección del artículo.

 

RESULTADOS Y DISCUSIÓN

 

El modelo por competencias en la UNAN-Managua presenta una estructura para la elaboración de un currículo basado en el desarrollo de competencias. El diseño curricular parte del análisis de las necesidades de formación en diferentes áreas de conocimiento. También se toma en cuenta 1as tareas profesionales relacionadas con cada carrera, lo que permite ajustar la oferta académica a las demandas del mercado laboral. Se identifican las competencias necesarias para cada carrera, abarcando tareas profesionales, campos de acción y esferas de actuación.

Este enfoque responde a la necesidad de mejorar la calidad educativa, adaptarse a los retos del siglo XXI, y cumplir con los objetivos del Programa Nacional de Desarrollo Humano y los Objetivos de Desarrollo Sostenible (Universidad Nacional Autónoma de Nicaragua Managua [UNAN-Managua], 2021).

Lo anterior coincide con Herrera (2023) quien afirma que “El nuevo modelo por competencias, quita muchos elementos que no eran necesarios para el estudiante, por ejemplo, varias clases generales que no aportaban al perfil profesional del educando, y solo quedaban como un requisito para poder seguir avanzando” (p, 159).
De igual forma, Herrera (2023) resalta que el enfoque basado en competencias optimiza el currículo educativo al estar centrado en los conocimientos y habilidades esenciales para el desarrollo profesional. Este modelo elimina contenidos generales que no aportan al perfil profesional, permitiendo una formación más específica y relevante. Como resultado, los estudiantes invierten tiempo en aprendizajes significativos, mejorando su preparación para el entorno laboral. Además, esta reestructuración curricular fomenta un mayor compromiso al alinear los contenidos con las demandas del mercado y la realidad profesional, asegurando que el aprendizaje tenga un impacto práctico y tangible.

En el modelo también se establecen los ejes verticales y horizontales del currículo, que integran componentes básicos, profesionalizantes e integradores. Incluye las indicaciones metodológicas para la organización de cada carrera. Define las funciones y responsabilidades de las diferentes comisiones curriculares en la UNAN-Managua, desde la comisión curricular central hasta las comisiones de carrera. Además, describe las modalidades de estudio, la organización del plan de estudios y las normativas de evaluación.

Lo que coincide con lo afirmado por Sáez (2010) el programa de asignatura es el documento de presentación en el que se indica el porqué de la existencia de la asignatura, lo que se desea lograr, lo que se pretende enseñar y la forma como se verificará el logro de los resultados, (cognoscitivos, procedimentales y actitudinales). Contenidos (competencias de aprendizaje, conocimientos, habilidades y valores), orientación de metodología de enseñanza y aprendizaje, recursos didácticos.

En relación al modelo educativo basado en competencias de la UNAN-Managua los docentes destacan que el enfoque coloca al estudiante en el centro del proceso de enseñanza-aprendizaje como se muestra en la Figura 1. Se aborda que el modelo está diseñado para responder a las necesidades específicas de la sociedad, retomando las demandas del mercado laboral nacional como internacional. También expresan que la metodología empleada busca integrar componentes curriculares de manera coherente, promoviendo la autonomía y responsabilidad de los estudiantes a través de un aprendizaje contextualizado y orientado a la resolución de problemas vinculados a su futura profesión.

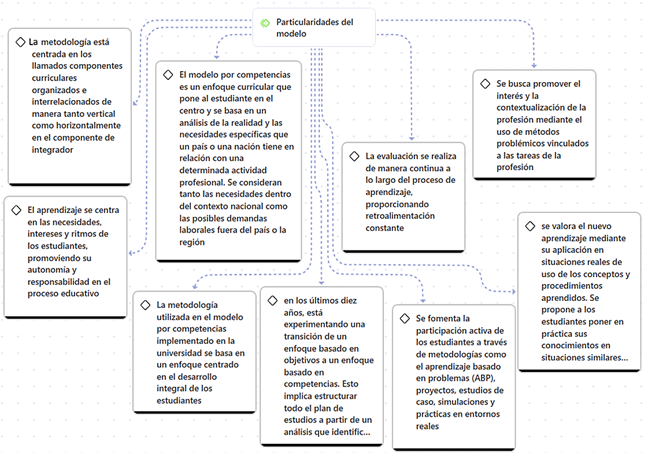
Figura 1.  Componentes establecidos en el modelo por competencias de la UNAN-Managua

En relación a lo expuesto en la Figura 1 se considera que el modelo por competencias enfatiza la evaluación continua, asegurando que el aprendizaje sea un proceso dinámico y retroalimentado constantemente. Este enfoque se adapta a los intereses y ritmos individuales de los estudiantes, orientando métodos activos y participativos que fomentan el desarrollo integral de sus capacidades. La finalidad es formar profesionales que no solo dominen los conocimientos técnicos, sino que también posean las habilidades necesarias para aplicarlos eficazmente en situaciones reales, tanto dentro como fuera de su contexto local.

Esto coincide con lo manifestado por Escoto (2022):

En relación a las competencias los maestros expresan Figura 2 que las competencias de aprendizaje abordan el dominio de los conceptos matemáticos y también enfatizan habilidades transversales como la resolución de problemas, la comunicación, el uso de tecnologías, y la capacidad para aplicar conocimientos en situaciones prácticas. Este enfoque busca preparar a los estudiantes para enfrentar desafíos académicos y profesionales, integrando tanto competencias específicas como habilidades generales esenciales para su éxito en el campo profesional.

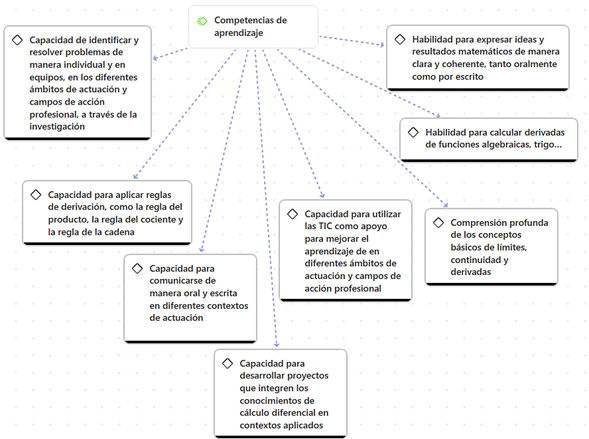
Figura 2.  Competencias establecidas en los componentes disciplinarios

Las competencias mencionadas reflejan un conjunto integral de habilidades cruciales para el desempeño académico y profesional en campos relacionados con las ciencias y la ingeniería. La capacidad para identificar y resolver problemas es fundamental, ya que permite a los estudiantes enfrentar desafíos complejos de manera autónoma o en equipo, utilizando un enfoque analítico que incluye la investigación y la aplicación de conocimientos previos. Esta competencia se complementa con la capacidad para aplicar reglas de derivación, que es esencial para resolver problemas matemáticos avanzados, facilitando la comprensión y manipulación de funciones en diferentes contextos.

Lo que coincide con lo orientado en el diseño curricular para desarrollar competencias en la [UNAN-Managua] (2021) debido a su relevancia, las competencias genéricas son definidas por la universidad en respuestas a las necesidades de la sociedad:

• Capacidad para comunicarse de manera oral y escrita en diferentes contextos de actuación.
• Capacidad de identificar y resolver problemas de manera individual y en equipos, en los diferentes ámbitos de actuación y campos de acción profesional, a través de la investigación.
• Capacidad de demostrar creatividad para hacer avanzar los diferentes ámbitos de actuación y campos de acción profesional donde se desempeña.
• Capacidad para utilizar las TIC como apoyo para mejorar el aprendizaje de en diferentes ámbitos de actuación y campos de acción profesional.
• Capacidad de comprender la realidad socio-económica, política e histórica del país y actuar en su desarrollo social. (p. 10)

Por otro lado, la capacidad para comunicarse de manera oral y escrita y la habilidad para expresar ideas y resultados matemáticos son competencias que garantizan que los estudiantes puedan transmitir sus conocimientos de manera clara y efectiva, tanto en contextos académicos como profesionales. El dominio de las TIC se convierte en un aliado estratégico en este proceso, permitiendo no solo la gestión y presentación de información, sino también la resolución de problemas complejos mediante herramientas digitales.

En cuanto al proceso de evaluación establecido para la óptima aplicación del modelo por competencias se ha establecido las directrices y procedimientos para la evaluación, promoción académica y el reconocimiento de equivalencias en la universidad. Lo que es fundamental para garantizar la transparencia y uniformidad en la manera en que se evalúa y promueve a los estudiantes dentro de la institución ([UNAN-Managua], 2021).

Se puede interpretar entonces que el proceso de evaluación establecido para la aplicación del modelo por competencias en la UNAN-Managua se caracteriza por su enfoque en la estandarización y la equidad. Al establecer directrices claras y procedimientos definidos para la evaluación, promoción académica y reconocimiento de equivalencias, la universidad busca asegurar que todos los estudiantes sean evaluados bajo los mismos criterios, lo que es esencial para mantener la transparencia y coherencia en el proceso educativo. Lo que facilita la comparación y el reconocimiento de competencias adquiridas por los estudiantes en diferentes contextos y también promueve un entorno académico en el que las oportunidades de progreso se distribuyen de manera justa y uniforme, alineándose con los principios de calidad educativa.

Esto coincide con lo expuesto por Aragón (2017):

El documento "Metodología para la Evaluación del Currículo por Competencias en la UNAN-Managua" describe un enfoque estructurado para la evaluación continua del currículo implementado en la universidad. Este enfoque se basa en un diseño curricular orientado al desarrollo de competencias, que busca responder a las necesidades cambiantes de la sociedad y mejorar la calidad académica. Se explica la importancia de la evaluación curricular para mejorar la calidad educativa, la cual está alineada con los Objetivos de Desarrollo Sostenible y el marco de cualificaciones. El currículo por competencias no solo busca formar en habilidades técnicas, sino también desarrollar profesionales con una visión integral, éticamente responsables y capaces de adaptarse a cambios ([UNAN-Managua], 2021).

En la metodología se destaca también la evolución de los procesos de transformación curricular en la UNAN-Managua desde 1992, destacando la participación de toda la comunidad universitaria en estos procesos y los avances logrados a lo largo de los años. El documento justifica la necesidad de realizar evaluaciones sistemáticas del currículo para asegurar su pertinencia, eficiencia y eficacia, y establecer objetivos de dicha evaluación, que incluyan la mejora continua y la alineación con las demandas del entorno.

También en la “Metodología para la Evaluación del Currículo por Competencias en la UNAN-Managua” se discuten las bases teóricas que sustentan el enfoque por competencias, enfatizando la formación integral y la necesidad de una educación que prepare a los futuros profesionales para enfrentar problemas reales con un enfoque crítico y contextual. Se define un sistema de dimensiones y aspectos que deben considerarse para evaluar el currículo, y se detalla la metodología a seguir para llevar a cabo esta evaluación, involucrando a todos los actores de la comunidad universitaria.

En esta misma línea López y Farfán (1998) afirman lo siguiente:

En definitiva, la Normativa de Evaluación ofrece una guía detallada para la evaluación continua del currículo en la UNAN-Managua, enfocada en asegurar que la formación por competencias cumpla con los estándares de calidad y responda efectivamente a las necesidades de la sociedad. Es decir, que tiene como objetivo principal regular las actividades de evaluación y calificación de los estudiantes que cursan estudios en diferentes modalidades (turno regular, por encuentros y a distancia). Esto incluye la asistencia, puntualidad, promoción académica, y el manejo de equivalencias de asignaturas para estudiantes que cambian de carrera o provienen de otras instituciones educativas.

Lo antes descrito coincide con Tobón (2004) que afirma lo siguiente:

Un aspecto central de la normativa es la evaluación basada en competencias, que orienta el proceso de aprendizaje hacia el logro de competencias específicas. Este enfoque permite una evaluación más objetiva y reduce la subjetividad en la calificación. La normativa establece que la evaluación debe ser continua, multivariada y multidimensional, utilizando diferentes técnicas e instrumentos para recopilar evidencias del desempeño estudiantil.

En relación a lo expuesto León (2017) afirma que la conceptualización y operacionalización del aprendizaje significativo de la matemática y la formación de competencias profesionales, en los estudiantes son las variables del proceso de formación. En ese sentido, se va de lo general a lo particular, de tal forma que sea posible entenderlas y comprenderlas.

Se observó que todo lo normado y establecido para el proceso de evaluación en modelo por competencia de la UNAN-Managua, enfatiza la importancia de seleccionar adecuadamente las técnicas de evaluación. Esto implica que pueden utilizarse observaciones, grupos focales, pruebas de ejecución y portafolios, entre otros. Estos instrumentos deben estar alineados con las competencias que se desean evaluar.

Según Flores (2017) estas actividades deben de tener un orden interno entre sí, en ese sentido se recomienda que estas deben hacer que el estudiante realice actividades diversas, no solo ejercicios rutinarios y monótonos, más bien acciones que vinculen sus conocimientos y experiencias previas, con interrogantes que provengan de lo real con la información objeto de conocimiento. Es decir, el proceso evaluativo no debe obviar la elaboración de secuencia didácticas, dado que es un eje central que siempre debe ir de la mano en la planificación didáctica.

La normativa para el proceso de evaluación define las condiciones bajo las cuales los estudiantes pueden ser promovidos al siguiente nivel académico. Esto está estrechamente relacionado con la evaluación de las competencias adquiridas y el rendimiento académico demostrado durante el curso. También aborda el sistema de registro de calificaciones, estableciendo procedimientos claros para asegurar la correcta documentación y validación de las evaluaciones realizadas. También orienta secciones dedicadas a disposiciones especiales y transitorias que podrían aplicarse en circunstancias excepcionales, asegurando la flexibilidad y adaptación a diferentes contextos educativos ([UNAN-Managua], 2021). 

El diseño curricular busca no solo formar profesionales competentes en su campo, sino también ciudadanos capaces de enfrentar desafíos sociales, culturales, y ambientales, con una visión integral y sistémica. La formación por competencias en la UNAN-Managua enfatiza el desarrollo de habilidades críticas, éticas y de autogestión, alineándose con las necesidades de una sociedad en constante cambio ([UNAN-Managua], 2021).

Se consultó también en relación al proceso de aplicación y evaluación del modelo por competencias como se muestra en la Figura 3. Lo manifestado por los docentes aporto elementos que se relacionan con lo establecido en la "Normativa de Evaluación, Promoción Académica y Equivalencias de UNAN-Managua 2021" para garantizar la calidad y equidad en el proceso educativo.

Al establecer un marco claro para la evaluación y promoción, esta normativa contribuye a un ambiente académico más transparente y justo, donde se promueve el desarrollo integral de las competencias en los estudiantes. Además, el enfoque en la evaluación por competencias asegura que el aprendizaje sea significativo y relevante, alineándose con los estándares modernos de educación superior.

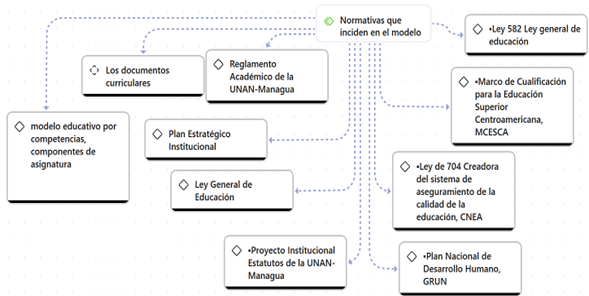
Figura 3.  Normativas que rigen el modelo por competencias en la UNAN-Managua

La Figura 3 muestra cómo un modelo educativo no solo se basa en decisiones internas de las instituciones, como los documentos curriculares y reglamentos, sino que también debe alinearse con normativas nacionales e internacionales para asegurar estándares de calidad y pertinencia. Esto garantiza que el modelo educativo responde tanto a las exigencias legales como a las necesidades del contexto local y regional. De acuerdo con [UNAN-Managua] (2021), diversas directrices, como los Objetivos de Desarrollo Sostenible (ODS), la Agenda 2030 y las conferencias regionales de educación superior, ofrecen pautas para que las universidades mejoren continuamente la formación profesional con un fuerte compromiso social y pertinencia regional.

En el ámbito metodológico para las carreras de ingeniería, los componentes de Matemática recomiendan iniciar con un diagnóstico de los conocimientos previos de los estudiantes, a incluir temas esenciales como funciones, pendiente de una recta, límite y continuidad de una función. Este diagnóstico permite identificar tanto las fortalezas como las debilidades conceptuales y procedimentales, lo que facilita la personalización de estrategias de aprendizaje y la identificación de áreas de mejora. Según Medina y Salvador (2009), la resolución de problemas estimula el pensamiento creativo y evita los aprendizajes memorísticos, favoreciendo un aprendizaje significativo.

Para fortalecer la comprensión teórica y práctica, se utilizan materiales de referencia que incluyan problemas contextualizados en el campo de la ingeniería. Estos libros de texto deben, presentar ejercicios aplicados y gráficos, ayudan a los estudiantes a conectar los conceptos matemáticos con situaciones reales, potenciando su relevancia en los sistemas productivos de la región. Gutiérrez (2019) sostiene que el desarrollo de habilidades matemáticas orientadas a la resolución de problemas es clave para promover el pensamiento matemático en los estudiantes y prepararlos para afrontar desafíos profesionales complejos.

La formación integral en las carreras de ingeniería exige una participación activa del estudiante, partiendo de sus preconceptos y orientada a la construcción de significado. El uso de Software, metodologías colaborativas y herramientas digitales facilita la comprensión de fenómenos matemáticos, fomenta valores como la comunicación y el respeto, y fortalece el pensamiento lógico, permitiendo modelar y resolver problemas contextualizados; todo ello con el objetivo de desarrollar habilidades aplicables al Cálculo Diferencial.

En este sentido la evaluación del aprendizaje en el Cálculo Diferencial debe ir más allá de la obtención de respuestas correctas, centrándose en la comprensión profunda y justificación de los procesos y resultados, lo que facilita la consolidación de un aprendizaje significativo. Es fundamental que el sistema de evaluación sea de carácter procesual, considerando el desempeño del estudiante en actividades como la resolución de problemas, análisis grupal, investigación y comprobación del manejo de aspectos teóricos y prácticos. Salgado (2005) enfatiza que la evaluación es clave para verificar si el estudiante ha alcanzado las competencias establecidas en cada unidad temática, alineando así el proceso evaluativo con los objetivos de aprendizaje.

En el desarrollo de los componentes de la asignatura, se recomienda el uso de recursos didácticos específicos como guías de trabajo, cuestionarios y el plan didáctico, complementados por herramientas tecnológicas como calculadoras científicas, computadoras y proyectores. Estas herramientas facilitan la presentación de contenidos y promueven una interacción más dinámica en el aula. Sin embargo, dado el carácter abstracto del Cálculo Diferencial, el uso exclusivo de recursos tradicionales puede resultar insuficiente para promover un aprendizaje profundo y contextualizado. Rojas (2021) señala que la integración de tecnologías interactivas y herramientas digitales en la educación superior es indispensable para fomentar el desarrollo individual y democratizar el acceso al conocimiento.

El uso de software matemático especializado, simulaciones interactivas y plataformas de aprendizaje adaptativo representa una oportunidad para que los estudiantes visualicen conceptos complejos y las relaciones con situaciones reales de su futura práctica profesional. Pino y Salazar (2018) destacan que las TIC, además de proporcionar recursos lúdicos, incrementan la confianza y motivación de los estudiantes, facilitando un aprendizaje autónomo y colaborativo. Las estrategias más efectivas deben incluir el aprendizaje basado en problemas y proyectos, integrando las TIC para promover el protagonismo del estudiante en su proceso de aprendizaje y facilitando el desarrollo de competencias claves para el siglo XXI.

En este contexto, la educación moderna requiere una renovación metodológica que integre herramientas digitales y estrategias innovadoras, permitiendo una mayor interacción en el proceso de enseñanza-aprendizaje. La combinación de recursos tradicionales y tecnologías avanzadas no solo mejora la comprensión de los conceptos, sino que también garantiza que el aprendizaje sea dinámico, relevante y aplicable al entorno profesional del estudiante.

Planes Didácticos Semestrales

En el proceso de enseñanza-aprendizaje se debe tener en cuenta que existe una fundamentación lógica y psicológica de todo el proceso, basada fundamentalmente en los principios de formación del estudiante. Por ello es necesario mantener un control secuencial, sin obviar la evaluación, que guie y facilité la toma de decisiones acertadas en todo momento.

Para una efectiva planificación didáctica es necesario un debate y una reflexión sobre la utilidad, interés e importancia de los contenidos actuales para un proceso de enseñanza-aprendizaje y mediada por las nuevas tecnologías y condicionada por las demandas sociales. Por lo general, los docentes prefieren atribuir las responsabilidades sobre el fracaso de enseñanza a los propios estudiantes, a sus actitudes y a su escasa formación matemática (Dullius, 2009).

Se observó que existe una correspondencia en la mayoría de los elementos entre el componente y las planificaciones didáctica de los docentes (un ejemplo de ello se muestra en la Figura 4). Es decir, se corresponde el programa de asignatura con la planificación didáctica. No se encontró diferencia en los objetivos generales planteados en el componente con los objetivos plasmados en la programación. En este sentido, son pocas las adecuaciones pertinentes realizadas, que favorecen el proceso de enseñanza-aprendizaje de los estudiantes.

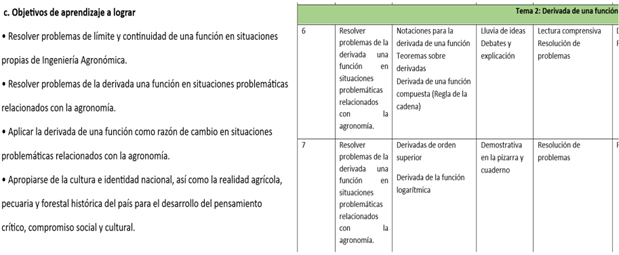
Figura 4.  Correspondencia componente y planificación didáctica.

Bournissen (2017), considera que la programación es esencial, para el desarrollo del proceso educativo y aplicar con éxito el modelo de formación por competencias. Es decir que todos los docentes necesitan realizar una buena programación de las clases que va a impartir. Esto es especialmente relevante si se desea poner a los estudiantes como centro del proceso de enseñanza-aprendizaje y conseguir que el aprendizaje sea atractivo y motivador.

Considerando que existen variadas estrategias, métodos y recursos pedagógicos que privilegian el aprender haciendo y para generar aprendizajes de manera preferentemente inductiva, contextualizada y práctica, es fundamental que su aplicación sea planificada con antelación, incorporando el uso de las TIC. Estos enfoques permiten que el estudiantado logre demostrar los conocimientos, habilidades, destrezas y valores propios del Cálculo Diferencial. En las Figuras 4, 5 y 6 se puede apreciar la falta de implementación de estos factores mencionados.

Esto coincide con lo manifestado por Novalbos (2016) el autor afirma que la programación comprende el tiempo, cantidad y orden en que se deben realizar las diferentes actividades, ejercicios y refleja en términos detallados la labor a realizarse por el docente. La programación previa de las clases permite una reflexión profunda en la asignatura a impartir durante el semestre y orienta a los docentes para desarrollar sus clases de manera atractiva, tranquila y también abierta, flexible y adaptable a los requerimientos, ajustes, cambios y mejoras que fueran necesarios de introducir.

En las planificaciones didácticas se observó que las estrategias de aprendizaje utilizadas son: lecturas comentadas, plenarias, resolución de problemas en la pizarra y cuadernos de los estudiantes y en pocos casos el uso de Software para la representación de funciones. Lo que indica una falta de implementación en el uso de herramientas TIC para facilitar el desarrollo, análisis y comprensión de los conceptos fundamentales del Cálculo Diferencial. En este sentido, no se está favoreciendo el aprendizaje activo y significativo en los estudiantes.

El acelerado desarrollo científico, generador de los avances en el campo de las TIC, hacen que la sociedad necesite de un hombre capaz de usar estas tecnologías para aprender a aprender a lo largo de toda la vida. Vivimos en la sociedad de la era digital donde la información y el conocimiento adquieren un valor cada vez mayor. (Rojas, 2021, p, 4)

Las evaluaciones de los contenidos de Cálculo Diferencial se realizan a través de cuestionario, preguntas dirigidas, aplicación de rúbrica en la resolución de problemas, listas de cotejo aplicadas a exposiciones. No se observó la integración de las herramientas TIC para dinamizar el proceso de evaluación y hacerlo más atractivo para los estudiantes. Las figuras 4 y 5 son claros ejemplos. 

En relación a las estrategias metodológicas y de evaluación lo manifestado por los docentes (Figura 4) refleja un enfoque educativo integral que combina métodos tradicionales, como clases expositivas y el uso de libros de texto, con estrategias más modernas y colaborativas, como el trabajo en grupo y el uso de recursos digitales.

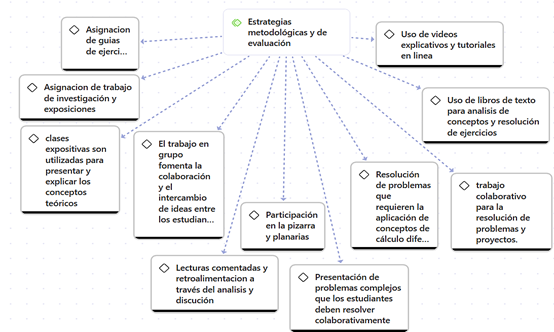
Figura 5.  Estrategias didácticas y de evaluación establecidas en el modelo.

Las estrategias de evaluación están diseñadas para ir más allá de la simple medición del conocimiento adquirido, promoviendo también el aprendizaje activo y la aplicación práctica de los conceptos. Esto refleja un esfuerzo claro por desarrollar competencias claves en los estudiantes, lo cual es esencial para prepararlos y que puedan enfrentar desafíos tanto académicos como profesionales con mayor confianza.

Las técnicas de evaluación son estrategias para la recopilación de evidencias sobe los resultados del aprendizaje logrado por los estudiantes. Esas permiten la identificación del desarrollo de las correspondientes competencias en un período de tiempo de formación: semestre, año o carrera. ([UNAN-Managua], 2021, p. 2)

La asignación de trabajos de investigación y exposiciones promueve la capacidad crítica y promueve la autonomía del estudiante en la búsqueda de información. En cuanto a la asignación de guías de ejercicios, el uso de libros de texto y la resolución de problemas favorecen el aprendizaje práctico, al aplicar los conocimientos adquiridos en situaciones controladas. Estas actividades teóricas se podrían complementar con el uso de TIC que proporcionan una forma dinámica para explicar conceptos complejos y facilitan el aprendizaje autónomo fuera del aula.

Los educadores tienen que afrontar el reto impuesto por los nuevos adelantos tecnológicos y apropiarse de las TIC, pues los mismos estudiantes crean continuamente necesidades de cambio al interactuar diariamente con nuevos instrumentos tecnológicos como nuevos computadores personales y telefonía móvil la cual es cada vez más amigable y versátil. (Restrepo y Jaramillo, 2011, p. 71)

El enfoque de evaluación mencionado, basado en cuestionarios, preguntas dirigidas, rúbricas para la resolución de problemas y listas de cotejo en exposiciones, cubre una gama tradicional de herramientas útiles para medir el aprendizaje. Sin embargo, es evidente la falta de integración de herramientas TIC en el proceso evaluativo (Figura 6), lo que representa una oportunidad desaprovechada para dinamizar y enriquecer la experiencia de los estudiantes. A continuación, se presentan evidencias de un componente desarrollado en segundo año de la carrera de Ingeniería Agronómica.

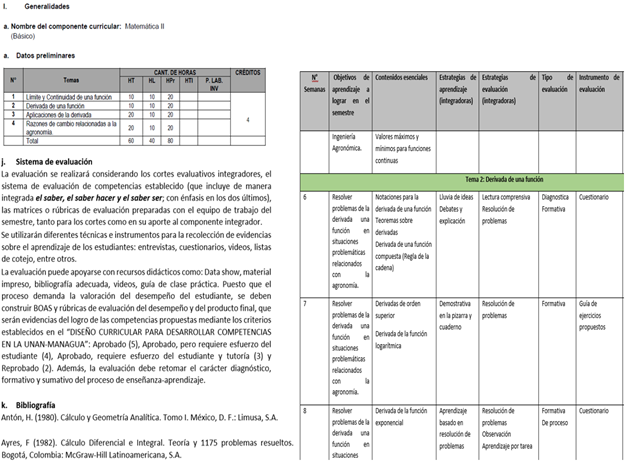
Figura 6.  Componente de Matemática II y planificación docente.

La incorporación de plataformas interactivas, aplicaciones de evaluación en tiempo real, y software especializado podría no solo hacer las evaluaciones más atractivas, sino también proporcionar retroalimentación inmediata y personalizada, fomentando un aprendizaje más participativo y activo. Estas herramientas tecnológicas permiten evaluar competencias de manera más integral, atendiendo a las necesidades de los estudiantes del siglo XXI, quienes tienden a responder mejor a entornos interactivos y digitales que les permitan aplicar los conceptos de manera práctica.

En relación a la integración de las TIC en la evaluación de los aprendizajes López (2006) considera que “Debemos plantearnos unos objetivos, una nueva forma de enseñar los contenidos, una nueva forma de evaluación, en definitiva, una nueva metodología con la que sacarle el mejor partido posible a las TIC” (p, 130). 
Se identificó que en parte los programas y planes didácticos relacionados con el Cálculo Diferencial en la UNAN-Managua/CUR-Estelí no han sido actualizados en los últimos años (Figura 7). Estos documentos aún recomiendan bibliografía que no integra enfoques contemporáneos ni el uso de herramientas digitales para facilitar la comprensión de conceptos claves como el límite, la continuidad y la derivada.

Figura 7.  Contenidos del componente Matemática II y bibliografía recomendada.

Esta situación representa una brecha entre el material disponible y las demandas actuales del entorno profesional, lo que limita la preparación de los estudiantes para enfrentar situaciones complejas en sus carreras.

Según Cárdenas et al. (2013), la actualización continua de los recursos didácticos es fundamental para garantizar la pertinencia y efectividad de la enseñanza. En contraste, la falta de renovación del contenido contribuye a métodos de enseñanza tradicionales, centrados en la repetición de ejercicios y en la memorización de procedimientos, en lugar de fomentar la resolución de problemas reales.

Percepciones de los Docentes sobre la Enseñanza del Cálculo Diferencial

El 90% de los Docentes entrevistados utilizan principalmente la resolución de guías de ejercicios como estrategia didáctica predominante. Aunque esta técnica tiene valor para el desarrollo de habilidades procedimentales, su uso exclusivo reduce las oportunidades de desarrollar competencias transversales como el pensamiento crítico, el análisis lógico y la creatividad. Pino y Salazar (2018) afirman que la integración de TIC en la enseñanza puede mejorar significativamente el aprendizaje, permitiendo a los estudiantes visualizar conceptos abstractos y aplicar sus conocimientos en situaciones prácticas.

Los datos muestran una disparidad significativa entre las estrategias propuestas en el modelo didáctico institucional y las prácticas reales de los docentes. Aunque el modelo promueve el aprendizaje activo y contextualizado, en la práctica prevalecen metodologías tradicionales, debido a la falta de formación continua en el uso de herramientas digitales y la resistencia al cambio por parte de algunos autores educativos (Revelo y Carrillo, 2018).

Esto evidencia la necesidad de reformar las prácticas docentes, incorporando estrategias más activas e innovadoras para el aprendizaje del Cálculo Diferencial. La escasez de recursos tecnológicos y la falta de capacitación docente constituyen barreras importantes que deben ser superadas para garantizar un proceso de enseñanza-aprendizaje más efectivo y alineado con las exigencias actuales.

La aplicación de metodologías como el aprendizaje basado en problemas y el uso de simulaciones interactivas podría transformar el proceso educativo, facilitando una comprensión más profunda de los conceptos matemáticos y mejorando el rendimiento académico de los estudiantes. Estas estrategias también permitirían desarrollar competencias esenciales para el ámbito profesional, como la toma de decisiones y la capacidad para resolver problemas complejos (Estrada et al., 2022).

Una de las principales dificultades identificadas en la enseñanza del Cálculo Diferencial es la naturaleza abstracta de sus conceptos, lo que dificulta la comprensión de los estudiantes. El 75% de los docentes mencionó que conceptos como el límite y la derivada resultan complejos debido a la falta de ejemplos prácticos y recursos visuales en el proceso de enseñanza. Según Estacio y Guerrero (2024), la incorporación de herramientas TIC facilita la comprensión de estos conceptos al ofrecer representaciones gráficas e interactivas.

Otro obstáculo significativo identificado fue la escasa formación docente en el uso de TIC. Aunque el 80% de los docentes reconocen la importancia de las TIC, solo el 30% afirmó sentirse capacitado para integrarlas en sus clases de manera efectiva. (Revelo y Carrillo (2018) destacan que la falta de capacitación continua limita la posibilidad de adoptar nuevas metodologías y herramientas tecnológicas.

A pesar de las dificultades, se identificaron oportunidades para mejorar el proceso de enseñanza. La implementación de estrategias basadas en el aprendizaje activo y colaborativo, así como la integración de simuladores matemáticos y plataformas interactivas, se presenta como una solución viable. Pino y Salazar (2018) destacan que estas herramientas no solo mejoran la comprensión de conceptos abstractos, sino que también fomentan la participación y el trabajo en equipo.

 

CONCLUSIONES  

 

La enseñanza del Cálculo Diferencial enfrenta importantes desafíos, principalmente relacionados con la naturaleza abstracta de sus contenidos y la limitada integración de TIC en el proceso de enseñanza-aprendizaje.

En la enseñanza aún prevalecen enfoques expositivos y mecanicistas, lo que dificulta la construcción de un aprendizaje significativo. Es imprescindible la adopción de metodologías activas, como el aprendizaje basado en la resolución de problemas en contextos reales, para mejorar la comprensión y aplicación del conocimiento matemático.

Se identificaron oportunidades significativas para transformar esta situación mediante la implementación de estrategias didácticas innovadoras y el fortalecimiento de la formación docente en competencias digitales.

Los libros recomendados presentan un desfase con respecto a los avances recientes en la didáctica del Cálculo Diferencial. Esta desactualización afecta la incorporación de enfoques pedagógicos innovadores y dificulta la adaptación a las necesidades actuales del aprendizaje, afectando la comprensión y aplicación efectiva de los conceptos matemáticos.

Se recomienda que las instituciones educativas inviertan en infraestructura tecnológica y diseñen programas de capacitación continua para los docentes, con el fin de promover la integración efectiva de las TIC. Asimismo, se sugiere el uso de herramientas interactivas y simuladores matemáticos para facilitar la comprensión de los conceptos clave del Cálculo Diferencial y fomentar el desarrollo de competencias transversales en los estudiantes.

 

REFERENCIAS BIBLIOGRÁFICAS