Propuesta metodológica para el proceso de enseñanza-aprendizaje del Álgebra en primer año de la Universidad
Methodological proposal for the teaching-learning process of algebra in the first year of the university
María Elena Blandón Dávila1
blandondavila@gmail.com
Recibido: 17 de diciembre de 2018, Aceptado: 22 de mayo de 2019
1 Doctora en Matemática Aplicada por la Universidad Nacional Autónoma de Nicaragua. Máster en Didácticas específicas de la Matemática, Universidad Autónoma de Barcelona-España.
RESUMEN
La presente investigación tuvo como objetivo general disponer de una propuesta metodológica para el aprendizaje significativo de los contenidos de la unidad de Álgebra como parte de la asignatura de Matemática General. Este estudio se realizó en los primeros años de dos carreras de la FAREM-Estelí, UNAN-Managua, en el período 2016-2017. Inició con una revisión documental sobre el tema de investigación, que permitió realizar la fundamentación teórica del mismo. Posteriormente, se procedió a la aplicación de los instrumentos de recogida de datos siendo estos, observación de clases, encuesta a estudiantes de los grupos involucrados en este proceso, grupo focal a estudiantes seleccionados, entrevistas a personal de dirección y docentes. Estas técnicas de investigación aplicada permitieron recopilar la información que luego fue categorizada y procesada para proceder al análisis de resultados. El aporte práctico de esta tesis es la elaboración de una propuesta metodológica que permita una mejor comprensión de los temas de Álgebra en los estudiantes. De igual manera, esta propuesta podrá ser utilizada por los docentes que imparten la asignatura de Matemática General.
Palabras claves: propuesta metodológica; proceso de enseñanza-aprendizaje.
ABSTRACT
The general objective of this research was to present a methodological proposal to help students achieve significant learning of the contents in the Algebra unit as part of the General Mathematics course. This study was carried out in the first years of two races of the FAREM-Estelí, UNITE-Managua, in the period 2016-2017. The research process started with a documentary review on the subject of research, which allowed to carry out the necessary theoretical foundation. Subsequently, data were collected through class observation, a survey to students in the selected groups, as well as focal groups, interviews with administrative staff, and teachers. These applied research techniques allowed the collection of data that were then categorized and processed to proceed to the analysis of results. The practical contribution of this thesis is the elaboration of a methodological proposal so that students achieve a better understanding of the Algebra. In the same way, this proposal can be used by the teachers who teach General Mathematics.
Keywords: methodological proposal; teaching-learning process.
INTRODUCCIÓN
La investigación educativa para el docente del siglo XXI señala una posición constructivista, dado que, se debe buscar que el estudiante aprenda haciendo su propio aprendizaje. El actual ritmo de renovación de estrategias exige un conocimiento de la utilización de saber cómo hacer. La renovación de estrategias se acelera tanto que va de la mano con la renovación tecnológica en la sala de clases, tanto como comunicativas en el desarrollo de la televisión, computadoras de alto nivel de velocidad para los diferentes “software” y las demás telecomunicaciones que se utilizan en las clases.
Cobra importancia destacar el potencial de la Matemática como campo de la investigación, que al igual que otras ciencias, requiere de los aportes de la misma desde dos grandes ámbitos:
La de desarrollos teóricos, es decir, los estudios referidos a la investigación pura (epistemología y estructura de la ciencia) que concretan la Investigación Matemática como un ciclo en el que las ideas se representan en forma abstracta, se manipulan estas abstracciones y se comprueban los resultados comparándolos con las ideas originales.
La de carácter práctico (la más cercana a los docentes en el aula), tal como su planificación, sus estrategias de enseñanza, la elaboración y utilización de recursos y la evaluación, entre otros aspectos que pudieran ser catalogados como de investigación aplicada y que estructuran la Investigación en Educación Matemática.
Una de las disciplinas que forma parte esencial de nuestra sociedad es la Matemática y su desarrollo responde al interés y deseo de resolver situaciones provenientes de los más variados ámbitos.
En la actualidad, la Matemática es una rama del saber que goza de un amplio prestigio social, debido a la asociación que se hace de ésta con el desarrollo científico y tecnológico.
Un estudiante de buen rendimiento en Matemática, es asociado a una persona capaz, con amplias perspectivas de desarrollo profesional. Pero para el común de los estudiantes, la Matemática sigue siendo una asignatura compleja, provista de un lenguaje críptico y de escasa significancia en su vida cotidiana.
La matemática es, sobre todo, saber hacer, es una ciencia en la que el método debe predominar sobre el contenido. Por ello, se debe insistir más en el desarrollo de los pensamientos propios que en la mera transferencia de contenidos, debido a que en este mundo que es muy cambiante, es mucho más valioso desarrollar procesos de razonamiento útiles, que memorizar una serie de conceptos que muy rápido se olvidan.
Es así que, el saber Matemática además de ser satisfactorio, es sumamente importante para interactuar con fluidez y eficacia en un mundo matematizado y la necesidad del conocimiento matemático crece día a día al igual que su aplicación.
En el proceso de enseñanza-aprendizaje de la Matemática, los conocimientos, las herramientas y las maneras de hacerla y comunicarla evolucionan constantemente.
Es por esta razón, que este proceso debe estar enfocado en el desarrollo de las destrezas necesarias para que el estudiantado sea capaz de resolver problemas cotidianos, fortaleciendo así el pensamiento lógico y creativo.
En este sentido, las estrategias desempeñan un papel fundamental, implican un cambio de paradigma, desde el conductista al del enfoque constructivista y al socioconstructivista que se caracterizan por que los estudiantes elaboran activamente significados gracias al rol mediador del docente.
En el ámbito educativo, las estrategias de aprendizaje significativo han sido uno de los focos de investigación más importantes, debido a que éstas facilitan un proceso de aprendizaje eficaz puesto que sirven de herramientas para la construcción de conocimientos y desarrollo de destrezas”. (Gutiérrez & Prieto, 1996, p. 50).
De igual manera, la mediación pedagógica ocupa un lugar privilegiado en cualquier sistema de enseñanza-aprendizaje. En el caso de la relación presencial es el docente quien debería actuar como mediador pedagógico entre la información a ofrecer y el aprendizaje por parte de los estudiantes.
Tomando en consideración que la sociedad contemporánea exige la constante renovación de las instituciones de Educación Superior, lo que implica transformaciones en la Docencia, Investigación, Extensión y Gestión Universitaria y la UNAN-Managua, consciente de su responsabilidad histórica, y de acuerdo con su Misión, asume el compromiso de formar profesionales mediante la gestión de un Modelo Educativo centrado en las personas, que contribuya con el desarrollo integral de los estudiantes. Este Modelo articula las acciones de los diferentes actores partícipes en el quehacer educativo de la Universidad y, orienta la formación de profesionales con una concepción científica y humanista, capaces de interpretar los fenómenos sociales y naturales con un sentido crítico, reflexivo y propositivo. Sus componentes esenciales son:
- Modelo Pedagógico.
- Modelo Curricular.
- Modelo Didáctico.
En los ejes rectores del modelo educativo se desarrollan aspectos relacionados con la misión, la visión, los valores, los ejes y objetivos estratégicos. (UNAN-Managua, Modelo Educativo, 2007, p.7).
Los métodos y procedimientos de investigación son los siguientes:
Métodos del nivel teórico
- Histórico y lógico: Para conocer el fenómeno objeto de estudio en sus antecedentes y tendencias actuales, en lo que respecta al desarrollo del proceso de enseñanza-aprendizaje.
- Analogía: Para la búsqueda de regularidades en el proceso de enseñanza-aprendizaje desde la visión de la asignatura de la Matemática General y de forma particular la unidad de Álgebra.
- El analítico-sintético, el inductivo-deductivo y el enfoque sistémico: Para estudiar las tendencias didáctico-metodológicas del proceso de enseñanza-aprendizaje de la Matemática en el nivel universitario y las particularidades de esta didáctica cuando se proponen estrategias metodológicas para la enseñanza-aprendizaje.
- Análisis documental: Para el estudio y análisis de la literatura especializada en torno al tema, documentos normativos vigentes, resultados de investigaciones afines e informes.
Métodos del nivel empírico
- La observación de clases, para determinar el desempeño de estudiantes y docentes en el proceso de enseñanza-aprendizaje.
- Entrevista, encuestas, y grupos focales para conocer criterios de docentes y estudiantes, buscar hechos que fundamentan la existencia del problema de investigación acerca del proceso de enseñanza-aprendizaje de los contenidos de la unidad de Álgebra y obtener información que permita utilizarlas en la propuesta metodológica.
La trascendencia de esta investigación está relacionada con el aporte en la elaboración de una propuesta metodológica activa-participativa contribuyendo a la motivación y generación de interés por el aprendizaje de la unidad de estudio.
En relación al aspecto metodológico, la propuesta elaborada estará disponible en un documento base para estudiantes y docentes. De igual manera, se considera que este estudio servirá de base para otras investigaciones que tengan como interés principal profundizar sobre la temática.
MATERIAL Y MÉTODO
El paradigma de la investigación
El presente estudio se realizó basado en el paradigma naturalista-humanista o interpretativo, teniendo como naturaleza ser dinámico, múltiple, holístico, construido y divergente. Este tiene como propósito, comprender e interpretar la realidad, los significados de las personas, interacciones y acciones.
Barrantes (2009), enfatiza en la comprensión e interpretación de la realidad educativa desde los significados de las personas implicadas en los contextos educativos. Aquí se requiere que el investigador utilice e interprete dos lenguajes, el propio y el de las personas que le proporcionan la información, a fin de interpretar de forma correcta lo que sucede en el contexto de la investigación.
El enfoque de la investigación
En el proceso de realización de la investigación la metodología utilizada de mayor predominio y presencia es el cualitativo, debido a que, utiliza la recolección de datos sin medición numérica para descubrir o afinar preguntas de investigación. Además se aplica la lógica inductiva de lo particular a lo general. Aunque se abordan algunos aspectos de índole cuantitativa (Hernández, Fernández & Baptista, 2014, p. 364).
Se partió del enfoque cualitativo en donde se inició con la observación a clases en primer año de las carreras de Física-Matemática y Psicología, luego se desarrollaron grupos focales en donde participaron estudiantes de las carreras antes mencionada, posterior se aplicó entrevista a docentes de ambas carreras, coordinadores y director de departamento. Se continuó con el enfoque cuantitativo en donde se aplicó encuesta a estudiantes participantes en este proceso. Aplicar los dos enfoques, permitió como investigadora usar técnicas cualitativas y cuantitativas.
De acuerdo al contexto, la investigación es no experimental, se caracteriza porque no hay manipulación de la variable independiente, no se asignan al azar los grupos. Solo se observan los cambios que ocurren. (Baena, 2014, p.12).
Por su finalidad la investigación es aplicada. De acuerdo con Baena (2014), la investigación aplicada, concentra su atención en las posibilidades concretas de llevar a la práctica las teorías generales, y destinan sus esfuerzos a resolver las necesidades que se plantean la sociedad y los hombres.
Por su alcance temporal es un estudio de tipo transeccional o transversal. Los estudios transversales pueden realizarse a la vez con varias realidades y muestras equivalentes que compartan características similares para poder obtener conclusiones más precisas que aumenten la posibilidad de generalizarlas a un mayor número de casos. Por ejemplo, se pueden estudiar a la vez varios grupos de alumnos de un mismo nivel académico y de distintos centros para analizar los factores que influyen con más probabilidad en su adaptación y rendimiento académico. (Martínez, 2007, p. 29).
Población y muestra
La población y la muestra fue seleccionada en base a criterios previamente definidos. Este estudio por razones de accesibilidad y conveniencia de la investigadora se realizó en la Facultad Regional Multidisciplinaria (FAREM-Estelí). Corresponde a cinco docentes y 98 estudiantes de primer año de las carreras de Física-Matemática y Psicología que cursan Matemática General en el I semestre 2017. Cabe señalar que las carreras antes indicadas se ofertan en otras Facultades de la UNAN-Managua.
La muestra la conforman 95 estudiantes del año y carreras antes mencionadas, distribuidos en 49 de la carrera de Física-Matemática y 46 de Psicología, dos docentes que facilitaron la asignatura durante el primer semestre 2017, un director del departamento de Ciencias de la Educación y Humanidades, dos coordinares de carrera.
La muestra es no probabilística, conocida también como guiada por uno o varios propósitos. El muestreo utilizado fue por conveniencia denominado también intencional, de voluntarios o por oportunidad. Para Hernández et al (2014, p. 386), la elección de las muestras no probabilísticas no depende de la probabilidad, sino de causas relacionadas con las características de la investigación o los propósitos del investigador.
Descripción de las etapas de la investigación
Revisión bibliográfica y documental: Se recopiló información teórica, en los diversos documentos y textos que abordan la temática de investigación.
Observación a clases: Dirigida a los grupos de estudiantes de primer año de las carreras de Física-Matemática y Psicología. Con estas observaciones se recopiló información respecto a la conducción del proceso enseñanza-aprendizaje, para ello se elaboró guía de observación.
Encuesta: Se aplicaron encuestas a los estudiantes de los dos grupos sujetos de estudio.
Grupos focales: Se realizaron dos grupos focales en la que participaron estudiantes de las carreras antes indicadas.
Entrevista: Se aplicó a docentes, director de departamento, coordinadores de carrera.
La información recopilada mediante los instrumentos antes indicados estuvo encaminada al desarrollo del proceso enseñanza-aprendizaje de los contenidos de la unidad de Álgebra, lo que posterior permitió realizar el análisis respectivo y triangular información.
RESULTADOS Y DISCUSIÓN
Se presentan los resultados obtenidos de la investigación a partir del procesamiento, análisis e información recopilada, los que se resumen a continuación.
Se analizó el rol de docentes y estudiantes en el desarrollo del proceso de aprendizaje, así como la motivación, en este último son muchos los factores que inciden tal como la habilidad que tiene el docente para la conducción del proceso, el entusiasmo, el interés por la materia, la percepción de su utilidad, es pues que la motivación tiene una influencia importante en el aprendizaje.
En las observaciones realizadas a clases, se hace referencia a la relación de los contenidos desarrollados con los conocimientos previos de los estudiantes, contextualización de estos, fomento de la comunicación docente-estudiante, estudiante-estudiante, motivación al estudiantado utilizando diversas técnicas, desempeño del rol de facilitador de procesos.
De acuerdo a lo observado en las sesiones de clases se constató que los docentes relacionan los contenidos con los conocimientos previos. La comunicación docente-estudiante en todas las clases observadas fue muy buena.
Se motiva al estudiantado para que comprendan los contenidos desarrollados, utilizan recursos didácticos, tales como tarjetas, guías de trabajo, orienta preguntas, algunas de estas las realiza de forma directa.
Se encontraron debilidades en los estudiantes en el dominio de conceptos fundamentales, por ejemplo, reducir términos semejantes, resolver ecuaciones, entre otros.
En lo que respecta a la resolución de problemas aplicados a los contenidos de Álgebra en la planificación y desarrollo de las clases, se observó muy poco.
Al ser consultados los estudiantes sobre el uso e importancia de las TIC, manifestaron no haber utilizado estas, pero las consideran que son de gran importancia.
La evaluación la realizan de forma sistemática en el transcurso de la clase, ya sea mediante preguntas orales, trabajos orientados en casa, trabajos realizados en equipo en el período de clases, ejercicios resueltos por los estudiantes en la pizarra.
En las entrevistas realizadas a autoridades expresan que los docentes cumplen con el desarrollo de los contenidos que están orientados en el programa de asignatura, señalando que debido a las dificultades con que vienen los estudiantes de secundaria, los maestros hacen repaso de los contenidos y con mayor énfasis en Álgebra ya que es de generaciones que los estudiantes tienen gran rechazo por esta temática.
Expresan que una de las dificultades grandes que se tiene es que los estudiantes no leen, y por ende se les dificulta la comprensión. “No es tan fácil cambiar la conducción del proceso enseñanza-aprendizaje, pero los maestros debemos buscar estrategias de aprendizaje en la que los estudiantes se involucren y se contextualicen los contenidos, se debe hacer uso de los saberes científicos y matemáticos para afrontar los diversos desafíos”.
Los docentes que formaron parte de la muestra señalaron que es necesario realizar una buena planificación de las clases, en donde se utilicen diferentes estrategias y recursos didácticas, se contextualicen los temas a fin de que se logre un aprendizaje significativo, pero también es fundamental que los estudiantes lean los materiales de estudio orientados, puedan aclarar sus dudas consultando diferentes fuentes bibliográficas o buscando ayuda personalizada. “Se debe hacer uso de los saberes científicos y matemáticos para afrontar los diversos desafíos”
Al preguntarles a los estudiantes en el grupo focal si las metodologías activas utilizadas por los docentes en el desarrollo de los contenidos de la unidad de Álgebra de la asignatura de Matemática General les permiten comprender con facilidad los contenidos que se abordan en la clase; los estudiantes manifestaron que algunas veces, sobre todo cuando usa material didáctico y es un tema que recuerdan de secundaria, pero los “los contenidos de Álgebra han sido bien áridos desde que los vimos en secundaria, y tuvimos que aprendernos las reglas de los productos notables y casos de factorización de memoria, entonces los olvidamos con facilidad y esto nos está afectando ahorita que estamos en la universidad”.
Cuando se les consultó sobre los principales recursos didácticos utilizados por los docentes en el aula de clases al facilitar los contenidos de la unidad de Álgebra correspondientes, respondieron que “en la unidad de Álgebra más que todo las guías de ejercicios que llevan los docentes, tarjetas, papelógrafo, la calculadora en menor medida, folletos”.
En base al análisis de las encuestas realizadas se seleccionaron algunas preguntas y gráficos cuyos resultados se presentan a continuación.
Gráfico 1: Uso de recursos didácticos
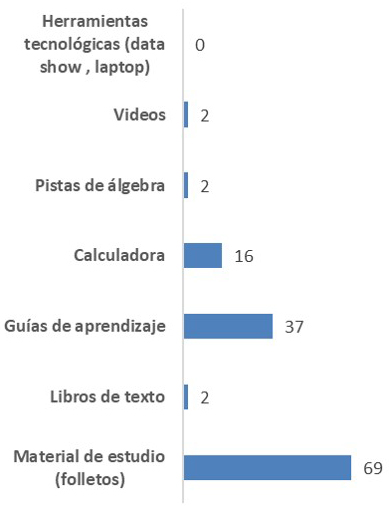
Fuente propia
Llama la atención el recurso didáctico más utilizado para el desarrollo del proceso de aprendizaje por los docentes son los folletos.
En la pregunta referida a las principales dificultades que se han encontrado en la asimilación de los contenidos de Álgebra, indicaron desmotivación por la incomprensión de los contenidos, deficiencia en los contenidos previos. El Álgebra la ven muy compleja, aunque se aborda primero la unidad de Aritmética no hay un cambio en el pensamiento del estudiante, poca aplicación en la vida real, expresaron “no encontramos en la práctica donde aplicar estos contenidos por eso se vuelven áridos, a veces uno que otro ejemplo que se aplica a la geometría”. El empleo de las ecuaciones para la resolución de problemas cuesta mucho, pasar del lenguaje común al lenguaje algebraico “poco entendemos, no interpretamos mucho cómo hacerlo”.
Referente a la importancia de los contenidos abordados en Álgebra en su mayoría expresan que son de utilidad
Gráfico 2: Importancia de los contenidos abordados en la unidad de Álgebra
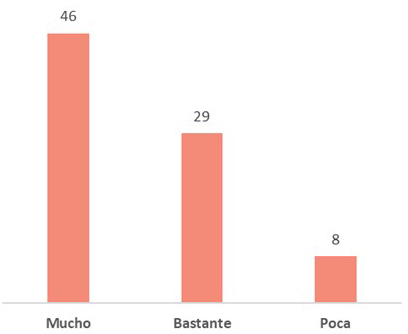
Fuente propia
En lo que respecta a la metodología utilizada por los docentes en el desarrollo de las clases se reflejan los resultados en el siguiente gráfico.
Gráfico 3: Valoración de la metodología utilizada por los docentes
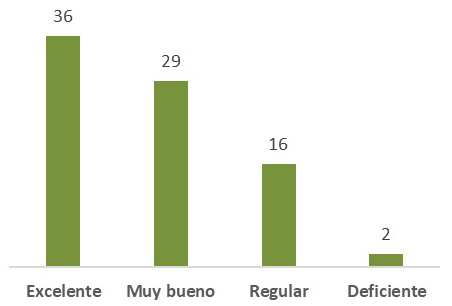
Fuente propia
Al consultarles sobre las estrategias didácticas utilizadas con mayor frecuencia cuando imparte los contenidos de Álgebra, respondieron lo siguiente:
Gráfico 4: Estrategias didácticas

Fuente propia
En la guía de encuesta se orientó a los estudiantes resolver una serie de ejercicios.
A continuación, se muestra ejemplos con sus resultados.
Reduzca la expresión
![]()
Tabla No. 1. Número de estudiantes que lo resolvieron de la forma:
| Correcta | Incorrecta | En parte | No lo resolvieron |
| 16 | 22 | 21 | 24 |
Fuente propia
Se presentan los procedimientos más comunes utilizados por los estudiantes para resolver el ejercicio.
Al solicitarles que determinaran el valor numérico de la expresión ![]() , las respuestas obtenidas fueron:
, las respuestas obtenidas fueron:
Tabla No. 2. Número de estudiantes que lo resolvieron de forma:
| Correcta | Incorrecta | En parte | No lo resolvieron |
| 17 | 12 | 19 | 35 |
Fuente propia
Algunas formas que lo resolvieron
![]()
![]()
Al plantearles que resolvieran el siguiente binomio ![]() , los resultados fueron los siguientes:
, los resultados fueron los siguientes:
Tabla No. 3. Número de estudiantes que lo resolvieron de forma:
| Correcta | Incorrecta | En parte | No lo resolvieron |
| 8 | 23 | 20 | 32 |
Fuente propia
Algunas respuestas obtenidas
![]()
![]()
![]()
![]()
Esto conlleva a concluir que hay falta de análisis antes de resolver los ejercicios, no tienen dominio de la ley de los signos y se adolece de patrones que les permitan que cuando resuelven ejercicios hagan uso de estos y los asocien, caso específico la forma en que se suma y resta en Aritmética.
Es fundamental la visión ampliada del Álgebra como instrumento de modelización matemática que se puede y debe ir construyendo progresivamente desde los primeros niveles educativos.
Aunque el cálculo literal, basado en las propiedades estructurales de los conjuntos numéricos se suele iniciar en secundaria, los procesos de simbolización, expresión de relaciones, identificación de patrones, son propios de los primeros niveles de alegorización, y como hemos visto en los resultados obtenidos por décadas los docentes que facilitamos la asignatura de Matemática en los distintos niveles pueden, y deben iniciarse desde la educación primaria.
CONCLUSIONES
Se constató que los docentes en su planificación tomaron en cuenta lo indicado en el modelo educativo, retomaron estrategias metodológicas propuestas en el mismo, así como el roll del docente y del estudiante en el aula de clases.
Los docentes prepararon cierto tipo de material didáctico para el desarrollo de las clases, pero para que este desempeñe su verdadero papel de hacer más dinámica y comprensiva la clase. Es fundamental los conocimientos previos de los estudiantes y el estudio constante, así como incorporar otros tipos de materiales didácticas acorde a los temas que se desarrollan.
Se constató a través de la observación a clases, encuesta y grupo focal que los estudiantes tienen dificultades en el dominio de temas básicos.
Aunque los docentes hacen grandes esfuerzos por utilizar metodologías activas, se continúa trabajando en parte con el método tradicional (pizarra, cuaderno, esquemas, resúmenes y resolución de ejercicios).
Entre Aritmética y Álgebra debe existir una correspondencia, pero la práctica dice que no es así, dado que, se limita el aprendizaje del Álgebra solo como una generalización de la Aritmética olvidando que hacer Álgebra no es solo hacer explícito lo que se encuentra implícito en la Aritmética.
En los ejercicios de productos notables y casos de factorización los estudiantes no logran discriminar cuando se le presentan los ejercicios frente a qué caso están. También se constató que hay grandes dificultades en la aplicación de las leyes de los exponentes. De aquí que es fundamental trabajar a profundidad la modelación matemática, así como la discriminación visual.
Se debe potenciar las posibilidades que ofrecen las TIC para lograr un aprendizaje que permita desarrollar competencias existentes en los estudiantes.
Los estudiantes tienen poco dominio de la calculadora, expresaron que en secundaria no les permitían el uso en clase, significa entonces que los docentes tenemos un reto y es enseñar a los estudiantes este recurso.
En suma, la visión que parece tener los estudiantes sobre el Álgebra, está enfocada exclusivamente a la generalización de algunos procesos aritméticos que estudiaron en el nivel secundario.
Se concluye esta investigación con la elaboración de la propuesta metodológica en donde se abordan los contenidos de la unidad de Álgebra.
BIBLIOGRAFÍA
Baena Paz, G. (2014). Metodología de la investigación México: Patria. Recuperado de goo.gl/yrcG31.
Barrantes, R. (2009). Investigación: Un cambio al conocimiento, un enfoque cuantitativo y cualitativo. San José, Costa Rica: UNEC.
Gutiérrez, F. & Prieto, D. (1996). Mediación Pedagógica (3a ed.). Guatemala: IIME/EDUSAC.
Hernández, F. & Soriano, E. (1997). La enseñanza de las matemáticas en el primer ciclo de la educación primaria: Una experiencia didáctica. España: Universidad de Murcia.
Martínez, A. (2007). La investigación en la práctica educativa: Guía metodológica de investigación para el diagnóstico y evaluación de los centros educativos. Madrid: FARESO, S. A. Recuperado de goo.gl/ZLE0h
UNAN-Managua. (2011). Modelo educativo, Normativa y Metodología para la planificación curricular. Managua: Editorial Universitaria. Tutecotzimí.
© 2019 - Revista Científica de FAREM-Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
