
https://revistas.unan.edu.ni/index.php/Multiensayo
DOI: https://doi.org/10.5377/multiensayos.v11i22.20839
Aplicación de la Estadística Inferencial en la investigación de Contextos Educativos
Application of Inferential Statistics in Educational Contexts Research
Jolbin José Mairena Aráuz
Universidad Nacional Autónoma de Nicaragua, Managua. Centro Universitario Regional de Estelí. UNAN-Managua/CUR-Estelí, Nicaragua
https://orcid.org/0009-0003-5906-1748
jolbinjosemairena@gmail.com
Yesner Yancarlos Briones Rugama
Universidad Nacional Autónoma de Nicaragua, Managua. Centro Universitario Regional de Estelí. UNAN-Managua/CUR-Estelí, Nicaragua
https://orcid.org/0009-0008-4112-7784
yesneryancarlosbrionesrugama@gmail.com
Keren Jasmina González González
Universidad Nacional Autónoma de Nicaragua-León, Centro Universitario Regional de Somoto. UNAN-León/CUR-Somoto, Nicaragua
https://orcid.org/0009-0009-3079-6760
gkerenjasmina@yahoo.com
RECIBIDO
26/05/2025
ACEPTADO
03/07/2025
RESUMEN
En el mundo actual, saturado de datos, la clave no es sólo observar la información, sino ser capaz de hacer predicciones e inferencias: aquí es donde entra en juego la estadística inferencial. En la investigación científica, la estadística es una herramienta indispensable para contrastar hipótesis, identificar patrones y generar nuevos conocimientos. A diferencia de la estadística descriptiva, que se limita a la presentación de datos, la estadística inferencial permite generalizar sobre toda la población a partir del análisis de una muestra, con un margen de error controlado y un nivel de confianza determinado. El ensayo tiene como objetivo analizar los fundamentos teóricos, las herramientas metodológicas y los aspectos aplicados de la estadística inferencial, especialmente en el campo de las matemáticas. También se destaca su importancia para aumentar la fiabilidad y objetividad de la investigación científica.
PALABRAS CLAVES
Estadística inferencial; investigación científica; hipótesis; muestra; análisis de datos.
ABSTRACT
In today’s data-saturated world, the key is not only to observe information, but to be able to make predictions and inferences: this is where inferential statistics come into play. In scientific research, it is an indispensable tool for testing hypotheses, identifying patterns, and creating new knowledge. Unlike descriptive statistics, which is limited to the presentation of data, inferential statistics allow generalizations to be made about the entire population based on the analysis of a sample with controlled error and a given confidence level. This essay aims to analyze the theoretical foundations, methodological tools, and applied aspects of inferential statistics, especially in the field of mathematics. It also highlights its importance in increasing the reliability and objectivity of scientific research.
KEYWORDS
Inferential statistics; scientific research; hypothesis; sample; data analysis:
INTRODUCCIÓN
En un mundo lleno de datos, la verdadera pregunta no es qué se ve, sino qué se puede predecir a partir de lo que se observa: ahí es donde la estadística inferencial cobra vida. En la investigación científica, la toma de decisiones basada en datos se ha convertido en una herramienta fundamental para validar hipótesis, establecer relaciones y crear nuevos conocimientos. En este contexto, la estadística inferencial desempeña un rol fundamental al permitir que los investigadores extraigan conclusiones a partir de muestras representativas, con un margen de error controlado y un nivel de confianza establecido.
A diferencia de la estadística descriptiva, que se limita a resumir los datos observados, la también llamada inductiva va más allá al proporcionar métodos para hacer generalizaciones sobre una población entera (Mayorga-Ponce et al., 2020). Esta capacidad de inferir, predecir y valorar la incertidumbre la convierten en un pilar esencial de la indagación científica, social, económica y educativa.
El presente ensayo tiene como objetivo analizar las principales aplicaciones de esta disciplina en el proceso investigativo, abordando sus fundamentos teóricos, herramientas metodológicas y usos más relevantes en distintas áreas del conocimiento especialmente en matemática. Asimismo, se pretende evidenciar cómo esta disciplina contribuye a la generación de resultados válidos, confiables y extrapolables, fortaleciendo el rigor y la objetividad de los estudios.
La motivación para realizar este análisis surge de la necesidad de comprender y aplicar adecuadamente los métodos inferenciales en el proceso investigativo, especialmente en un entorno donde los datos son cada vez más abundantes y complejos (Herrera Castrillo, 2023). Para alcanzar estos fines, se adoptará una metodología de revisión teórica y análisis reflexivo, a partir del estudio de literatura especializada, ejemplos prácticos en los que la estadística inferencial ha desempeñado un papel decisivo en la obtención de conclusiones científicas. Con ello, se busca no solo profundizar en su importancia técnica, sino también destacar su valor como instrumento clave para el avance del conocimiento.
Metodológicamente, este ensayo se basa en una revisión documental de tipo narrativa con enfoque analítico, seleccionando literatura reciente (2019–2024) que discute las implicaciones del uso de la estadística inferencial en contextos educativos. La revisión permitió establecer relaciones entre los fundamentos teóricos y su aplicabilidad en distintas etapas del proceso investigativo
DESARROLLO
Estadística
La estadística es el puente entre la información que se tiene y el conocimiento profundo de dichos datos. En general, es una rama de las matemáticas cuya función es recopilar, organizar, analizar, interpretar y presentar datos con el propósito de proporcionar fundamentos claros y precisos para la toma de decisiones. Según Veiga et al. (2020), la estadística es una metodología científica que permite la elección entre diferentes opciones o formas posibles de resolver una situación de la vida cotidiana de modo que sea más efectiva y racional ante la incertidumbre, lo que la cambia en una herramienta indispensable en distintos campos del conocimiento.
Su aplicación en el campo de la investigación permite transformar información aparentemente caótica en conocimientos útiles para comprender fenómenos, descubrir patrones y hacer predicciones. Gracias a la estadística, se pueden realizar estudios que analicen muestras representativas y, a partir de los resultados obtenidos, inferir en conductas o particularidades de una población más amplia. Como afirman Suárez et al. (2020), la estadística ofrece las herramientas necesarias para comprobar hipótesis y respaldar científicamente los hallazgos de una investigación.
Además, no solo permite describir los datos, sino también establecer relaciones entre variables, identificar tendencias y evaluar la confiabilidad de los resultados. En este sentido, la estadística inferencial cobra mayor relevancia, puesto que facilita concebir generalizaciones más allá de los datos observados (Herrera Castrillo, 2019; Gil-Velázquez, 2020). Por ello, Mayorga et al. (2020) sostienen que esta disciplina permite inferir disoluciones válidas a través del análisis de una muestra, lo que la hace un elemento esencial para cualquier estudio exhaustivo.
Asimismo, no solo aborda un grupo de datos, sino que establece relaciones entre varios grupos. Por consiguiente, puede ser que solo se conozca una parte del o los grupos de datos a estudiar. Cualquiera que sea el caso existen ciertos pasos para el análisis estadístico los cuales se muestran en la siguiente figura:
Figura 1 Pasos del análisis estadístico
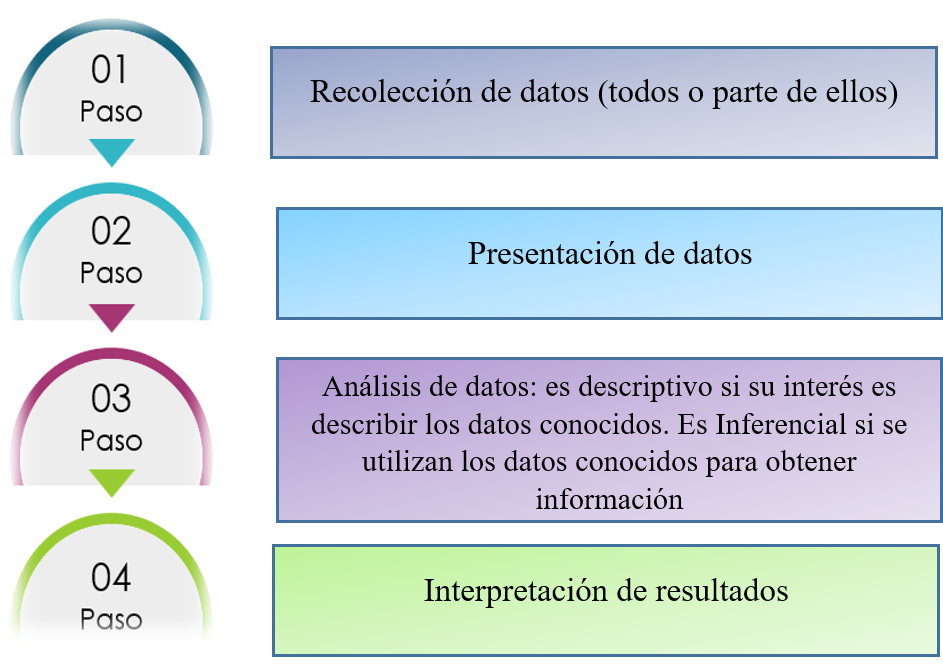
Nota. La figura muestra los cuatro pasos de un análisis estadístico. Fuente: creación de los autores.
De acuerdo con el análisis de datos que se necesite realizar, existen dos tipos de estadística: estadística descriptiva: consiste en realizar descripciones de un conjunto de datos conocidos y estadística inferencial que para fines de este trabajo se cubrirá con mayor realce.
Estadística inferencial
En muchos casos, es imposible determinar los valores de una variable para toda la población, por lo que debe utilizarse una parte de ella para analizar su comportamiento. La estadística inferencial ayuda a identificar la significancia de los resultados obtenidos; es decir, permite generalizar, predecir o extraer conclusiones sobre toda la población a partir del análisis de una muestra representativa. (Vásquez Sánchez y Ortiz Basauri, 2022). Metafóricamente, es como una lupa científica que, al observar una pequeña muestra, revela verdades ocultas sobre una gran realidad.
Su objetivo es tomar decisiones o hacer inferencias con base en los datos recopilados, valorando el grado de confianza y el margen de error. Para Castillo (2020), la inferencia estadística consiste en métodos que toman los resultados obtenidos de una muestra para estimar propiedades de una población completa. Esta área es fundamental en la investigación, porque “ayuda a los investigadores a proyectar decisiones hacia un contexto más amplio, con respaldo cuantitativo.
En síntesis, la estadística inferencial consiste en estudiar una parte de un conjunto de datos para obtener información sobre todo el conjunto. En otras palabras, determina en qué grado la información obtenida en un subconjunto de datos puede ser generalizada a todo el conjunto. Ese subconjunto de la población se define seguidamente.
Figura 2 Concepto de estadística inferencial
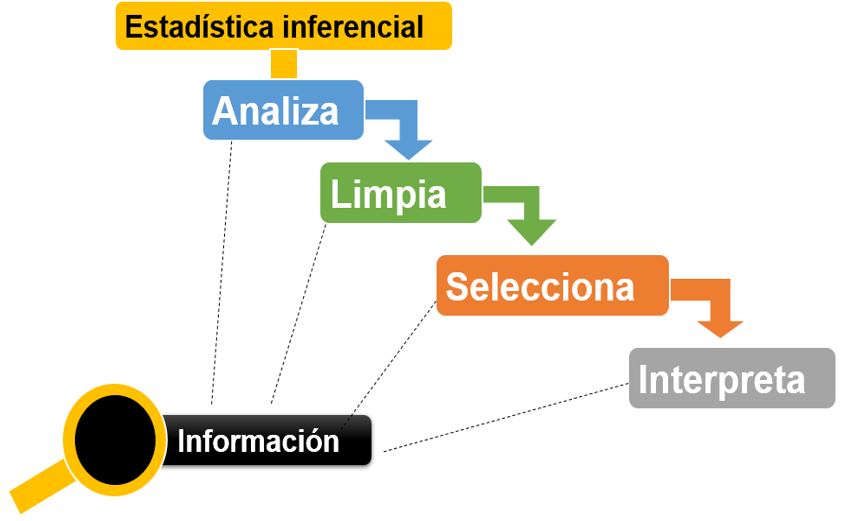
Nota. La figura muestra la directriz de la estadística inferencial. Fuente: creación de los autores.
Muestra:
Es una parte de la población. Esta se utiliza cuando la población es muy grande o imposible de cubrir en su totalidad, por ejemplo: cuando no se cuenta con los recursos económicos ni el tiempo, cuando la población es muy homogénea y el nivel de confianza es el apropiado para los fines que se persiguen, o cuando la unidad de estudio se destruye o transforma al ser examinada.
Figura 3 Selección de la muestra
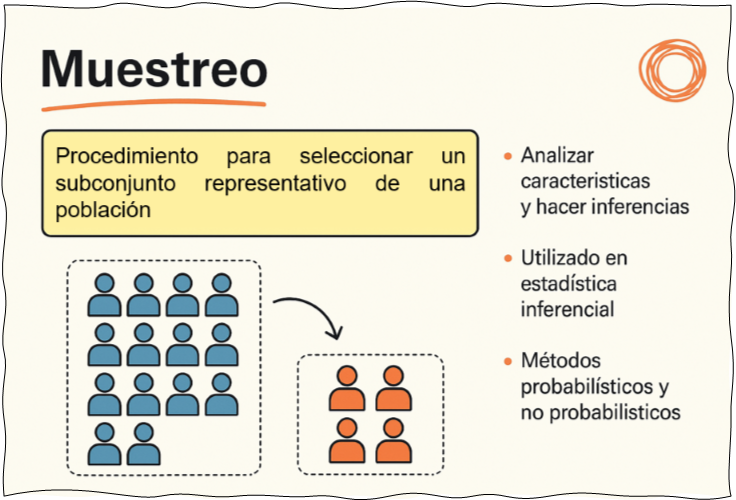
Nota. La figura menciona los tipos de muestreo. Fuente: creación de los autores
Cañas y Galo (2022) resaltan que no es posible plantear un problema científico si las variables que rigen la investigación no son medibles, tampoco se puede formular una hipótesis sin considerar un diseño para su verificación, de igual forma, realizar inferencias sin tener conocimiento de la distribución de las variables. Es importante considerar estas directrices en la investigación científica dado que el proceso de contrastación de la hipótesis que se propone en la ciencia empírica está condicionado al manejo de datos que surgen de los acontecimientos o fenómenos, información que se recoge de muestras representativas y pertinentes aplicando muestreos de acuerdo a como se distribuyen las unidades muestrales, en las que las variables a examinar serán medidas utilizando instrumentos válidos y confiables, que permita la prueba lógica y el análisis de inferencias en la población tal como se observa en la siguiente figura.
Tamaño muestral
Para determinar la idoneidad del tamaño de la muestra en un estudio, es necesario considerar no solo la varianza de la población (diversidad poblacional), sino también otros dos factores importantes: el nivel de confianza y el error máximo permisible en las estimaciones (error de muestreo). Como principio general, se puede afirmar que cuanto más homogénea sea la población, menor será el tamaño de la muestra requerido. Una vez determinados los parámetros poblacionales, el tamaño de la muestra se calcula utilizando diversos criterios estadísticos. Uno de ellos es la denominada fórmula "n" (tamaño de la muestra). Por lo tanto, para poblaciones infinitas, el cálculo de la muestra se puede realizar mediante la siguiente ecuación:
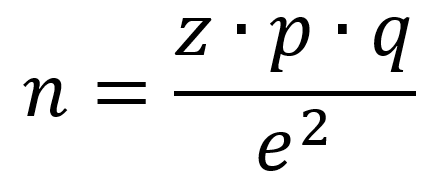 (1)
(1)
Donde:
n = tamaño de la muestra
z = nivel de confianza seleccionando por el investigador. Es una constante para 99%; equivale a 2,58.
p = probabilidad de éxito
q = probabilidad de fracaso
e2 = error máximo de estimación (seleccionado por el investigador, funciona como un resorte: a mayor error de estimación menor número muestral y a menor error de estimación mayor será el número muestral.
También hay fórmulas especiales para poblaciones finitas, en las que se introduce un error de estimación calculado sobre la base del tamaño de la población. Es así como, para poblaciones finitas, el cálculo de la muestra se puede realizar aplicando la fórmula representada en la siguiente ecuación:
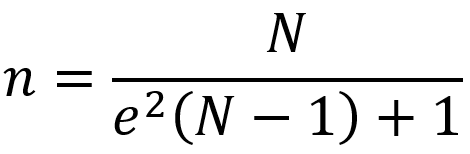 (2)
(2)
Donde:
n = tamaño de la muestra
N = población
e = error de estimación
Por ejemplo, si la población está integrada por 120 sujetos, considerando un error de estimación de 0,09, se tiene:
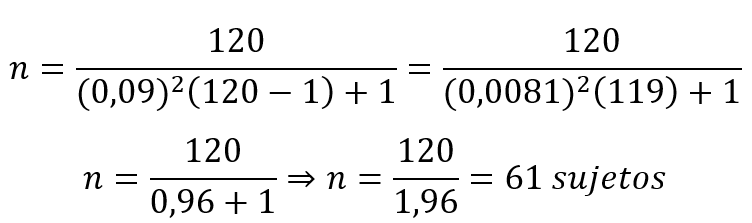
Muestreo
El proceso de seleccionar un grupo de elementos, individuos u objetos de una población que se consideren representativos, con el fin de estudiar sus características y luego hacer generalizaciones sobre toda la población, se denomina muestreo. De acuerdo con Hernández (2021) el muestreo está condicionado al tipo de investigación y fundamentalmente al diseño para la contratación de las hipótesis, dado que cada muestreo tiene diferente metodología, por lo tanto, éstos pueden ser probabilístico y no probabilístico.
Tal como se mencionaba anteriormente, existen diversas tipologías de muestreo, tanto probabilísticos (como el aleatorio simple, estratificado o sistemático) como no probabilísticos (por conveniencia, juicio o bola de nieve), y su votación obedece del propósito del estudio y de los recursos disponibles. Como señalan Mercado y Coronado (2021), “la validez de una investigación depende en gran medida de la calidad de la muestra seleccionada y de la técnica de muestreo empleada” (p.82). Por ello, un muestreo adecuado es la base sobre la cual se construyen inferencias confiables y científicamente sustentadas.
En el contexto de la estadística inferencial, el muestreo permite aplicar herramientas matemáticas para estimar parámetros poblacionales, probar hipótesis y calcular probabilidades, basándose únicamente en los datos de una muestra. Por tanto, todo proceso de investigación debe tener una visión clara sobre este aspecto en específico, ya que una muestra bien seleccionada proporciona estimaciones válidas sobre una población, siempre que se utilicen métodos estadísticos adecuados y se reconozca el error de muestreo. Esto implica que los resultados obtenidos mediante el análisis de la muestra pueden ser generalizados con un grado aceptable de confianza y precisión.
Enfoque de una investigación
Por otro lado, la orientación metodológica que adopta un investigador para abordar un problema o fenómeno de estudio se conoce como enfoque de la investigación, y está determinado por la forma en que se concibe la realidad, el ambiente de los datos que se desean seleccionar y los métodos de análisis utilizados. Existen principalmente tres enfoques: cuantitativo, cualitativo y mixto. Cada uno posee características, procesos y finalidades diferentes, lo cual implica que el tipo de enfoque elegido debe estar en conexión con los objetivos de la investigación. Acosta (2023) señala que el enfoque define el camino a seguir en el proceso investigativo, desde la recolección de datos hasta la interpretación de los resultados, lo que demuestra su relevancia en la planificación científica.
El enfoque cuantitativo se basa en el cálculo del objetivo de fenómenos, utilizando herramientas estadísticas para describir y analizar relaciones entre variables. Este enfoque busca explicar y predecir comportamientos por medio del análisis numérico de datos, frecuentemente obtenidos mediante encuestas, experimentos o análisis de bases de información. Es esencialmente ventajoso cuando se requiere probar hipótesis, generalizar resultados a una población determinada o evaluar el impacto de una intervención. Hernández (2021) indica que en el enfoque cuantitativo, el investigador prueba teorías mediante la examinación de las relaciones entre variables medibles, expresadas numéricamente y analizadas con procedimientos estadísticos. Esto lo transforma en la base de la estadística inferencial, ya que permite inferir resultados de una muestra hacia una población más amplia (Hernández-Sampieri & Mendoza Torres, 2020).
En cambio, el enfoque cualitativo se centraliza en la intuición profunda de fenómenos complejos, desde la perspectiva de los involucrados, explorando significados, percepciones y experiencias. Este tipo de investigación es flexible, interpretativa y utiliza métodos como entrevistas, grupos focales u observaciones. Mientras que el enfoque cuantitativo pretende generalizar, el cualitativo busca comprender la singularidad y riqueza del fenómeno estudiado. Finalmente, el enfoque mixto combina los métodos de ambos modelos, integrando datos cuantitativos y cualitativos para lograr una perspectiva más completa del problema de investigación. Según Franco y Vera (2020), “el enfoque mixto representa una tercera vía que permite superar las limitaciones de los métodos puramente cuantitativos o cualitativos” (p. 58), promoviendo una investigación más integral y sólida.
Alcance de una investigación
Imagine que el proceso de investigación es como un vasto océano, lleno de posibilidades y diversas respuestas por descubrir. No obstante, al igual que un marinero debe establecer un rumbo claro para evitar perderse, el alcance de la investigación actúa como esa brújula que define hacia dónde se dirige el estudio, qué se va a explorar y qué se va a dejar de lado. Establecer límites no figura restringir el conocimiento, sino dirigir la mirada en lo esencial para poder ahondar de manera efectiva en el tema elegido, guiando el proceso de forma clara y precisa.
En otros términos, se refiere a la profundidad y nivel de generalización con los que se abordará un fenómeno de estudio. Este concepto está estrechamente unido con los objetivos que se pretenden alcanzar, puesto que establece los lineamientos y la intención del investigador al desarrollar un trabajo científico. Tal como lo expresan Arias et al. (2020), “el alcance de una investigación depende del estado del conocimiento sobre el tópico y de los objetivos esbozados, puesto que de ello se deriva la estrategia metodológica a seguir” (p. 91). En relación a lo anterior, dependiendo del propósito del estudio, se identifican cuatro tipos principales de alcance: exploratorio, descriptivo, correlacional y explicativo.
Ahora bien, un estudio exploratorio se aplica cuando el problema de investigación es poco conocido o no ha sido abordado con anterioridad. Su función principal es familiarizarse con el fenómeno, identificar variables relevantes y esbozar hipótesis futuras. En cambio, el alcance descriptivo busca especificar las propiedades, particularidades y perfiles de individuos o situaciones, proporcionando una imagen precisa del fenómeno en estudio. Como lo indica Sampieri et al. (2014), “los estudios descriptivos miden de forma independiente conceptos o variables para ofrecer una visión detallada del objeto de análisis” (p. 92).
Por otra parte, los estudios correlacionales tienen como objetivo establecer la relación o grado de asociación entre dos o más variables, sin manejar directamente. Finalmente, los estudios con alcance de tipo explicativo buscan reconocer las causas de los fenómenos y establecer relaciones de causalidad. Son los más complejos y profundos, debido a que pretenden responder al porqué de los acontecimientos. En palabras de Cañas (2022), “los estudios explicativos se centran en probar hipótesis y construir teorías que expliquen fenómenos mediante relaciones causa-efecto” (p. 67). Por consiguiente, el alcance de la investigación no solo orienta el tipo de diseño metodológico que se debe utilizar, sino que también condiciona la interpretación y utilidad de los resultados obtenidos
Todo lo anterior da lugar a lo siguiente: La estadística inferencial desempeña un papel fundamental en la realización de investigaciones porque permite realizar generalizaciones y conclusiones sobre toda la población a partir de una muestra preseleccionada. Dependiendo del tipo de alcance de la investigación, la estadística inferencial puede influir de diferentes maneras: En pocas palabras es una herramienta clave que permite generalizar los resultados de una muestra a contextos más amplios, independientemente del alcance de la investigación.
Figura 4 Influencia de la inferencia estadística en el alcance de una investigación
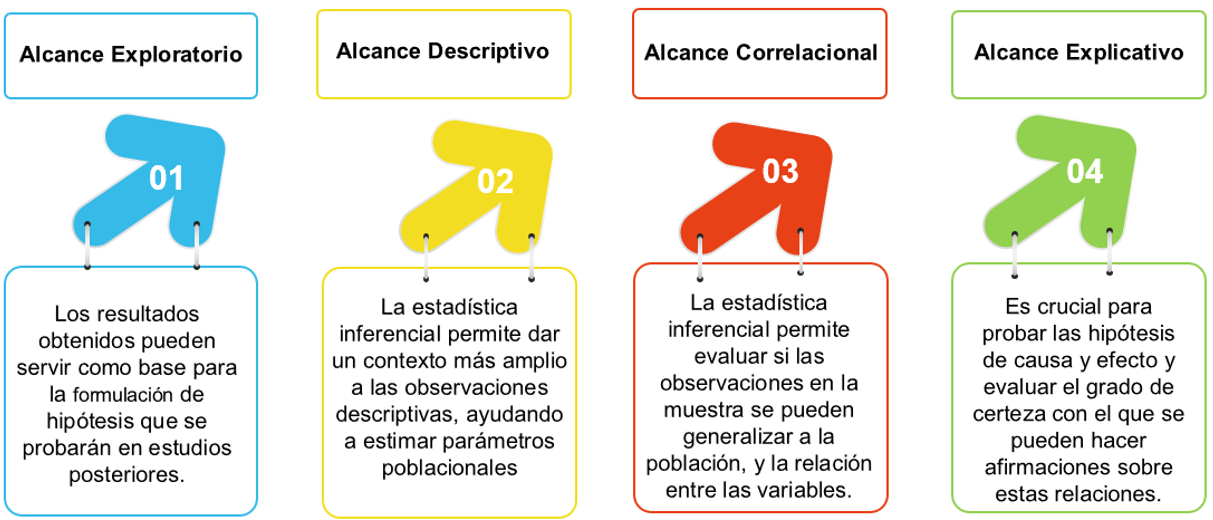
Nota. La figura describe los alcances de la Estadística Inferencial. Fuente: Creación propia
Diseño de investigación
Los tipos de diseño de investigación se clasifican según el grado de control del investigador sobre las variables y el propósito del estudio. En general, existen tres tipos principales, como se muestra en la Tabla 2:
Tabla 1 Tipos de diseños de investigación
| No experimental | Cuasi - experimental | Experimental |
|---|---|---|
| el investigador observa los fenómenos tal como se dan en su contexto natural, sin manipular variables, siendo común en estudios descriptivos y correlacionales | implica cierta manipulación de variables, pero sin un control total del entorno ni asignación aleatoria | el investigador manipula una variable experimental no comprobada, bajo condiciones estrictamente controladas. Su objetivo es describir de qué modo y por qué causa se produce o puede producirse un fenómeno |
Nota. La tabla describe los tipos de diseño de la investigación. Fuente: creación de los autores
Según Pereyra y Vaira (2021), “el diseño de investigación depende del grado de control que se tenga sobre las variables y del propósito que se desea alcanzar con el estudio”
La estadística inferencial influye en estos diseños, de modo que extrae conclusiones sobre un objeto en estudio a partir de datos obtenidos de muestras, lo que fortalece la validez y difusión de los resultados Guevara et al. (2020). Además, su uso varía según el tipo de diseño. En el diseño experimental, se aplican técnicas como el análisis de varianza, pruebas t y modelos de regresión para comparar grupos y evaluar los efectos de las variables independientes sobre las dependientes.
En los diseños no experimentales, se emplean correlaciones y regresiones simples o múltiples para analizar asociaciones. En todos los casos, la inferencia estadística permite ir más allá de la simple descripción de datos, aportando profundidad y solidez a las interpretaciones del estudio por lo que resulta de suma importancia para cualquier investigador que busque comprender, explicar o predecir fenómenos a partir de datos empíricos.
Paradigmas de investigación
Los paradigmas son el cuerpo de creencias, presupuestos, reglas y procedimientos que guían lo que se investiga y cómo se investiga. De Franco y Vera (2020), resaltan que un paradigma es una forma de representar objetivamente el conocimiento, un modelo que confirma una determinada forma de percibir la realidad, basada en un lenguaje específico y una forma característica de comprender el mundo. Entre los paradigmas más comunes en la investigación científica se encuentran los paradigmas con enfoques cuantitativos y cualitativos. (Rodríguez & Mendivelso, 2018).
En la tabla 3 se presentan las principales características de los tipos de paradigma:
Tabla 2 Características de los tipos de paradigmas
| Aspecto | Paradigma Positivista (Cuantitativo) | Paradigma Interpretativo (Cualitativo) |
|---|---|---|
| Fundamentos filosóficos | Se basa en el empirismo y el positivismo lógico. Defiende que el conocimiento se alcanza solo a través de la objetividad. Busca descubrir relaciones causales entre fenómenos. | Se apoya en la fenomenología y el enfoque interpretativo. Acepta la subjetividad como vía válida para conocer. El conocimiento se genera a partir de la interacción entre el investigador y el objeto de estudio. |
| Propósito de la investigación | Su objetivo es explicar, predecir y controlar fenómenos, así como comprobar teorías. Busca formular leyes generales independientes del contexto, mediante razonamiento deductivo. | Busca comprender e interpretar la realidad social, enfocándose en el significado que las personas dan a sus experiencias. Utiliza un enfoque inductivo centrado en la comprensión profunda. |
| Relación investigador-sujeto | El investigador mantiene una postura objetiva, distante y neutral. Observa los fenómenos desde fuera, sin intervenir para evitar sesgos. Teoría y práctica se consideran elementos separados. | Existe una interacción directa y cercana entre el investigador y los participantes. Se reconoce la interdependencia y se valora la retroalimentación entre teoría y práctica. |
| Técnicas e instrumentos | Utiliza herramientas cuantitativas como pruebas estandarizadas, cuestionarios, observaciones estructuradas y experimentos. | Se apoya en técnicas descriptivas cualitativas, donde el investigador actúa como el principal instrumento de recopilación y análisis. |
| Análisis de datos | Se realiza un análisis estadístico, tanto descriptivo como inferencial, basado en el manejo numérico de los datos. | El análisis se basa en la interpretación inductiva de los datos y en la triangulación de fuentes y perspectivas. |
Nota. La tabla menciona los tipos de paradigmas y sus características. Fuente: Stracuzzi y Pestana (2012)
Formulación de Hipótesis
Una hipótesis es una proposición que expresa una solución posible, lógica y comprobable a un problema. Es una respuesta preliminar a una pregunta de investigación y se formula como una generalización o afirmación. Una hipótesis puede comprobarse para determinar su validez (Stracuzzi & Pestana, 2012).
La formulación de hipótesis es una etapa fundamental dentro del proceso de investigación científica. Esta proposición o afirmación tentativa sobre la relación entre dos o más variables, puede ser puesta a prueba mediante procedimientos estadísticos. En la investigación cuantitativa, las hipótesis deben formularse de forma clara, específica y comprobable
Existen principalmente dos tipos de hipótesis:
- Hipótesis nula (H₀): plantea que no existe diferencia o efecto entre los grupos o variables. Es el punto de partida de la prueba estadística.
- Hipótesis alternativa (H₁ o Hₐ): sugiere que sí existe una diferencia, relación o efecto significativo entre las variables.
Por ejemplo:
- H₀ la aplicación de la estadística inferencial en la investigación no tiene impacto significativo en la precisión de los resultados obtenidos.
- H₁ la aplicación de la estadística inferencial en la investigación mejora significativamente la precisión de los resultados obtenidos.”
La primera hipótesis plantea que el uso de la estadística inferencial no mejora ni empeora la precisión de los resultados en comparación con otras metodologías de análisis. Sin embargo, la segunda sugiere que la aplicación de la estadística inferencial tiene un impacto positivo y significativo en la precisión de los resultados de la investigación, permitiendo hacer inferencias más confiables a partir de los datos muestrales.
La estadística inferencial influye directamente en la validación o rechazo de estas hipótesis. Gracias a diversas herramientas los investigadores pueden analizar datos muestrales y generalizar los resultados a toda una población, evaluando la probabilidad de que un resultado haya ocurrido por azar. A través del valor y el nivel de significancia , se determina si hay suficiente evidencia estadística para rechazar la hipótesis nula Manterola et al. (2019).
En este sentido, la inferencia estadística no solo aporta objetividad al proceso de toma de decisiones científicas, sino que también proporciona el fundamento matemático para determinar si los resultados percibidos en un estudio son estadísticamente relevantes Castillo (2020) Esto consolida la validez interna del estudio y da lugar a que los hallazgos puedan ser utilizados para mejorar teorías, políticas o prácticas en el área investigada.
Aplicaciones principales de la estadística inferencial en la investigación
Como se ha mencionado antes la inferencia estadística posibilita la formulación conclusiones generales sobre un conjunto a partir del estudio de un subconjunto (muestra) Cañas et al. (2022). Entre sus principales aplicaciones en la investigación destacan la estimación de parámetros poblacionales, la verificación de hipótesis y también el estudio de las relaciones entre variables. Este enfoque se caracteriza por la objetividad y la imparcialidad: el investigador adopta una postura externa e imparcial respecto al objeto de estudio, considerando al participante como tal. Mantiene cierta distancia para evitar la distorsión de los resultados, separando claramente la teoría de la práctica, considerándolas entidades separadas e independientes.
Según Stracuzzi y Pestana (2012), es clave en investigaciones cuantitativas porque facilita la validación mediante pruebas empíricas. Esta aplicación se amplía a campos como la psicología, educación, economía y ciencias sociales, donde se busca vislumbrar anomalías complejas a través del análisis de datos. Al mismo tiempo, Manterola et al. (2019) resaltan que su uso ha sido indispensable en investigaciones recientes sobre el cambio climático, la eficacia de vacunas y el comportamiento social ante crisis globales. En la siguiente tabla se muestran otras de sus aplicaciones en contextos educativos, como muestra ta tabla 4:
Tabla 3 Aplicaciones de la estadística inferencial en la investigación educativa
| Área | Aplicación e influencia de la estadística inferencial |
|---|---|
| Investigación educativa |
|
| Didáctica de la matemática |
|
| Evaluación del aprendizaje |
|
| Formación docente |
|
| Tecnología educativa |
|
| Educación inclusiva |
|
| Currículo y planificación |
|
| Educación matemática |
|
| Psicología educativa |
|
| Sociología de la educación |
|
Nota. La tabla describe la vinculación de la estadística inferencial con la investigación educativa. Fuente: (Roque Hernández, 2022)
Por lo tanto, la inferencia estadística como conjunto de técnicas del método Científico, proporciona instrumentos para la elección de diversas opciones cuando prevalecen las condiciones de incertidumbre. En la investigación científica, es primordial seguir ciertos estándares, puesto que la contrastación de hipótesis en la ciencia práctica depende del análisis de datos emanados de hechos o fenómenos. Éstos a su vez, se recogen de grupos específicos mediante técnicas de muestreo que consideran la distribución de las unidades muestrales. Las variables de interés se miden con instrumentos válidos y confiables, lo cual aprueba una demonstración lógica de la hipótesis y la inferencia a la población original, completando así el circuito del proceso de investigación tal como se observa en la figura.
Técnicas inferenciales utilizadas en investigaciones científicas, sociales y educativas
En la investigación científica, social y educativa, las técnicas inferenciales son piezas que hacen posible obtener conclusiones válidas sobre un conjunto amplio de individuos basándose en el estudio de un grupo representativo. Entre los métodos más comunes incluyen pruebas de hipótesis, intervalos de confianza, análisis de varianza, regresión lineal y pruebas no paramétricas. Estas técnicas posibilitan identificar relaciones entre variables, comparar grupos y evaluar el impacto de intervenciones, todo ello con un control estadístico que reduce el margen de error y favorece la validez de los resultados (Hernández Sampieri et al., 2014)
Tabla 4. Técnicas inferenciales y su aplicación por área
| Técnica Inferencial | Aplicación Principal | Área de Investigación |
|---|---|---|
| Prueba t | Comparar dos grupos | Psicología, Educación |
| ANOVA | Comparar más de dos grupos | Ciencias Sociales, Medicina |
| Regresión lineal | Predicción entre variables | Economía, Marketing |
| Chi-cuadrado | Asociación entre variables categóricas | Sociología, Ciencias Políticas |
| Intervalo de confianza | Estimar parámetros poblacionales | Ciencias de la Salud, Ingeniería |
Nota. La tabla menciona las técnicas inferenciales y el área de aplicación. Fuente: creación de los autores
Tabla 5 Finalidades de la estadística descriptiva y la estadística inferencial
| Estadística Descriptiva | Estadística Inferencial | |
|---|---|---|
| Generalidades | También es conocida como estadística deductiva | También es conocida como estadística inductiva |
| Finalidad | Describe lo que sucede en una muestra o conjunto de datos | Hacer generalizaciones y predicciones sobre una población |
| Aplicación | Tablas, gráficos, medidas de tendencia central y dispersión | Pruebas de hipótesis, intervalos de confianza, regresión |
| Técnicas utilizadas | Tablas, gráficos, medidas de tendencia central y dispersión | Pruebas de hipótesis, intervalos de confianza, regresión |
| Población vs. Muestra | Se enfoca directamente en los datos disponibles (muestra) | Usa la muestra para decir algo sobre toda la población |
Nota. La tabla describe generalidades de la estadística descriptiva e inferencial. Fuente: creación de los autores.
Diferencias entre estadística descriptiva e inferencial en el proceso investigativo
La estadística descriptiva y la inferencial se complementan, pero persiguen objetivos diferentes. Mientras la descriptiva proporciona un panorama general de los datos observados, la inferencial va un paso más allá para tomar decisiones o hacer afirmaciones sobre una población completa.
Sin embargo, la distinción clave entre ambas ramas radica en sus objetivos y alcances, la estadística descriptiva se limita a resumir y presentar datos observados, proporcionando un "escenario" del conjunto de datos. Por el contrario, la estadística inferencial va más allá al inferir en características y actitudes de una población completa a partir de una muestra. Es decir, la descriptiva nos dice "qué" muestran los datos recogidos, mientras que la inferencial nos ayuda a entender el "qué podría ser" para la población en general. Las dos son complementarias y su correcta aplicación es crítica para avalar la validez y confiabilidad de los resultados de un estudio de investigación.
Tabla 6 Comparación entre estadística descriptiva e inferencial
| Característica | Estadística Descriptiva | Estadística Inferencial |
|---|---|---|
| Propósito | Resumir los datos | Generalizar o inferir |
| Uso de muestras | Opcional | Obligatorio |
| Uso de probabilidad | No | Sí |
| Ejemplo | Promedio de edades | Estimar promedio poblacional |
Nota. La tabla describe las características de la estadística descriptiva e inferencial. Fuente: creación de los autores.
Partiendo de eso la estadística inductiva que es en la que se centra este trabajo presenta cierto beneficios y limitaciones a la hora de aplicarla en el proceso de investigación, como se refleja en la tabla 6:
Tabla 7 Beneficios y limitaciones de estadística inferencial
| Beneficios |
|
| Limitaciones |
|
Nota. La tabla menciona beneficios y limitaciones de la inferencial. Fuente: creación de los autores.
La Tabla 6 muestra que la estadística inferencial ofrece importantes ventajas, como la capacidad de tomar decisiones informadas basadas en datos estadísticos, el ahorro de recursos al trabajar con muestras y el aumento de la fiabilidad científica de la investigación y la comprobación de hipótesis. Sin embargo, sus resultados dependen de la representatividad de la muestra, y los errores de tipo I y tipo II pueden llevar a conclusiones incorrectas. Además, la aplicación incorrecta de los métodos reduce la fiabilidad de los datos obtenidos.
Importancia de la estadística inferencial en la investigación
Figura 5 Importancia de la estadística inferencial en la investigación
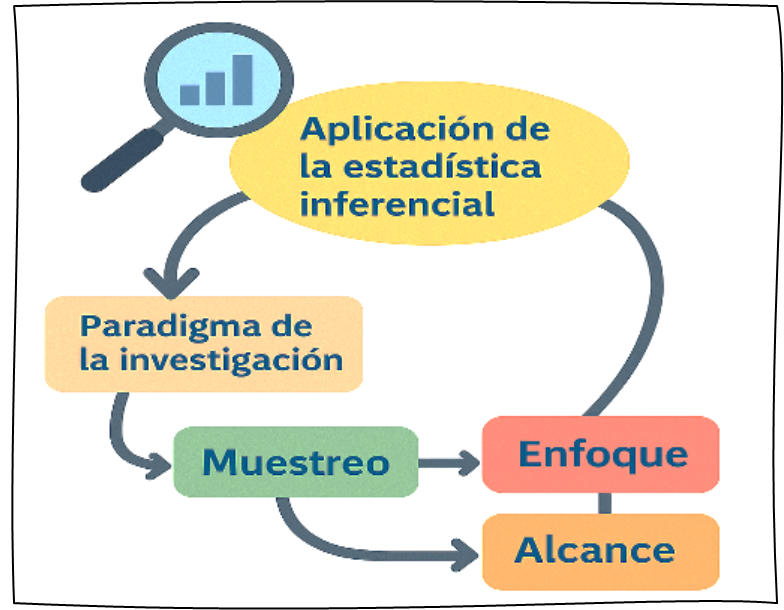
Nota. La figura muestra la importancia de la estadística inferencial en la investigación. Fuente: creación de los autores.
El esquema gráfico ilustra de forma visual y didáctica cómo la estadística inferencial se posiciona como un eje articulador dentro del proceso de investigación científica, relacionándose con componentes clave como el paradigma de la investigación, el enfoque, el muestreo y el alcance del estudio. La estadística inferencial depende de un muestreo adecuado, puesto que se basa en los datos de la muestra para hacer predicciones sobre la población total. Si el muestreo es sesgado, las inferencias serán poco confiables. Por consiguiente, esto define el nivel de profundidad del estudio ya sea de tipo: exploratorio, descriptivo, correlacional o explicativo.
Por otro lado, el paradigma figura como la base filosófica y cognitiva que orienta el estudio investigativo, influyendo desde la formulación del problema hasta la interpretación de resultados (de Franco & Vera Solórzano, 2020; Triminio-Zavala et al., 2024). Paradigmas como el positivista promueven el uso de enfoques cuantitativos, donde la estadística inferencial constituye una cosmovisión que guía las decisiones metodológicas de los investigadores. Mientras que el enfoque es el que determina la estrategia metodológica que puede ser: cuantitativa, cualitativa o mixta (Suárez Reynoso et al., 2020).
Por último, el componente alcance define la profundidad de los objetivos de investigación: exploratorio, descriptivo, correlacional o explicativo. A medida que el alcance avanza hacia lo explicativo, se requiere un mayor rigor inferencial para establecer relaciones entre variables Hernández y Ávila (2020). De este modo, la estadística inferencial conecta la visión epistemológica (paradigma), la estrategia metodológica (enfoque), la técnica de recolección (muestreo) y la profundidad del estudio (alcance). Su aplicación rigurosa permite garantizar la validez científica de los hallazgos de una investigación.
CONCLUSIONES
La estadística inferencial desempeña un papel esencial en la investigación desde sus inicios hasta la actualidad, en donde se siguen realizando inferencias sobre poblaciones a partir de datos muestrales, lo cual mejora la eficiencia, la validez y la aplicabilidad de los hallazgos científicos para la solución de un determinado problema o avances en diferentes áreas. Por ello, su aplicación en las ciencias sociales, educativas y naturales ha fortalecido la calidad de los estudios, aportando herramientas y descubriendo nuevas formas de concebir la realidad respecto a algo, destacando procesos como prueba de hipótesis, estimando ciertos parámetros para el análisis de información que unifique, cree y transforme. No obstante, se requiere que el investigador comprenda de manera rigurosa los fundamentos y restricciones para evitar interpretaciones erróneas. Todas las ideas expuestas aquí se resumen en la siguiente frase: "la estadística inferencial transforma datos en decisiones, permitiendo que las muestras hablen por poblaciones enteras y guiando el camino hacia conclusiones fundamentadas."
REFERENCIAS BIBLIOGRÁFICAS
Acosta Faneite, S. F. (2023). Los enfoques de investigación en las Ciencias Sociales. Revista Latinoamericana OGMIOS, 3(8), 82-95. https://orcid.org/0000-0003-2719-9163
Arias Gonzáles, J. L., Covinos Gallardo, M. R., & Cáceres Chávez, M. (2020). Formulación de los objetivos específicos desde el alcance correlacional en trabajos de investigación. Ciencia Latina Revista Científica Multidisciplinar, Ciudad de México, 4(2), 237-247. https://doi.org/10.37811/cl_rcm.v4i2.73
Cañas Escamilla, J. J., & Galo Sánchez, J. R. (2022). Estadística, probabilidad e inferencia. (J. G. Rivera Berrío, Ed.) Córdoba , España: Red Educativa Digital Descartes Interactivo. https://proyectodescartes.org/iCartesiLibri/index.htm
Castillo Riquelme, V. (2020). Enseñanza de la estadística inferencial mediante una aplicación móvil. Revista Latinoamericana de Investigación en Matemática Educativa, 23(2), 233 - 258. https://doi.org/10.12802/relime.20.2324
de Franco, M., & Vera Solórzano, J. L. (2020). Paradigmas, enfoques y métodos de investigación: análisis teórico. Mundo Recursivo, 3(1), 1-24. https://doi.org/https://atlantic.edu.ec/ojs/index.php/mundor/article/view/38/54
Gil-Velázquez, C. L. (2020). Los paradigmas en la educaciónEl aprendizaje cognitivo. UNO Sapiens Boletín Científico de la Escuela Preparatoria No. 1, 2(4), 19-22. https://repository.uaeh.edu.mx/revistas/index.php/prepa1/issue/archive
Guevara Alban, G. P., Verdesoto Arguello, A. E., & Castro Molina, N. E. (2020). Metodologías de investigación educativa (descriptivas, experimentales, participativas, y de investigación-acción). RECIMUNDO, 4(3), 163-173. https://doi.org/10.26820/recimundo/4.(3).julio.2020.163-173
Hernández González, O. (2021). Aproximación a los distintos tipos de muestreo no probabilístico que existen. Revista Cubana de Medicina General Integral, 37(3), 1-3. http://scielo.sld.cu/pdf/mgi/v37n3/1561-3038-mgi-37-03-e1442.pdf
Hernández González, O. (2021). Aproximación a los distintos tipos de muestreo no probabilístico que existen. Revista Cubana de Medicina General Integral., 37(3), 1-3. https://doi.org/http://revmgi.sld.cu/index.php/mgi/article/download/1442/453
Hernández Mendoza, S. L., & Avila, D. D. (2020). Técnicas e instrumentosde recolección de datos. Boletín Científico de las Ciencias Económico Administrativas del ICEA, 9(17), 51-53. https://repository.uaeh.edu.mx/revistas/index.php/icea/issue/archive
Hernández Sampieri, R., Fernández Collado, C., & Baptista Lucio, P. (2014). Definiciones de los enfoques cuantitativo y cualitativo, sus similitudes y diferencias. Metodología de la investigación, sexta edición. Mexico. https://apiperiodico.jalisco.gob.mx/api/sites/periodicooficial.jalisco.gob.mx/files/metodologia_de_la_investigacion_-_roberto_hernandez_sampieri.pdf
Hernández-Sampieri, R., & Mendoza Torres, C. P. (2020). Metodología de la investigación Las rutas cauntitativa, cualitativa y mixta. México: Mc Graw Hill. http://www.biblioteca.cij.gob.mx/Archivos/Materiales_de_consulta/Drogas_de_Abuso/Articulos/SampieriLasRutas.pdf
Herrera Castrillo, C. J. (2019). Estadística y Probabilidades | Física Matemática. UNAN-Managua / FAREM-Estelí. https://n9.cl/estadisticayprob
Herrera Castrillo, C. J. (2023). Interdisciplinariedad a través de la Investigación en Matemática y Física. Revista Chilena de Educación Matemática, 15(1), 31-45. https://doi.org/10.46219/rechiem.v15i1.126
Manterola, C., Quiroz, G., Salazar, P., & García, N. (2019). Metodología de los tipos y diseños de estudio más frecuentemente utilizados en investigación clínica. Revista Médica Clínica Las Condes, 30(1), 36-49. https://doi.org/10.1016/j.rmclc.2018.11.005
Mayorga-Ponce, R. B., Sillis-Palma, K., Martínez-Alamilla, A., Salazar-Valdez, D., & Mota-Velázquez, U. I. (2020). Cuadro comparativo “Estadística inferencial y descriptiva”. Educación y Salud Boletín Científico Instituto de Ciencias de la Salud Universidad Autónoma del Estado de Hidalgo, 8(16), 93-95. https://repository.uaeh.edu.mx/revistas/index.php/ICSA/issue/archive
Mercado Piedra , J. A., & Coronado Manqueros, J. M. (2021). El muestreo y su relación con el diseño metodológico de la investigación. Manual de temas nodales de la investigación cuantitativa. Un abordaje didáctico. Universidad Pegagógica de Durango, México. http://www.upd.edu.mx/PDF/Libros/Nodales.pdf
Pereyra, L. C., & Vaira, M. (2021). Diseño de Muestreo. Universidad de Jujuy, Argentina. https://ri.conicet.gov.ar/bitstream/handle/11336/156720/CONICET_Digital_Nro.765f1689-fa9b-4347-bf51-55265c8d3477_A.pdf?sequence=2
Rodríguez, M., & Mendivelso, F. (2018). Diseño de investigación de corte transversal. Revista Médica Sanitas, 21(3), 141-146. https://doi.org/10.26852/01234250.20
Roque Hernández, R. V. (2022). La enseñanza de la estadística para la investigación: algunas recomendaciones reflexionadas desde la praxis. Revista Educación, 46(2), 646-656. https://www.scielo.sa.cr/scielo.php?script=sci_arttext&pid=S2215-26442022000200646
Stracuzzi, S. P., & Pestana, F. M. (2012). Metodología de la investigación cuantitativa. Caracas: Fondo Editorial de la Universidad Pedagógica Experimental Libertador. https://gc.scalahed.com/recursos/files/r161r/w23578w/w23578w.pdf
Suárez Reynoso, C. A., Medrano Reynoso, E., & Suárez Reynoso, W. E. (2020). Metodología de la investigación y estadística inferencial de egresados de la Universidad Nacional del Centro del Perú, Huancayo 2019. Sendas, 1(4), 65 - 80. https://doi.org/10.47192/rcs.v1i4.52
Triminio-Zavala, C. M., Herrera-Castrillo, C. J., & Medina-Martínez, W. I. (2024). Formación investigativa del estudiante universitario en el Modelo por competencia de UNAN-Managua. Revista Científica Estelí, 12(48), 108–128. https://doi.org/10.5377/farem.v12i48.17529
Vásquez Sánchez, E., & Ortiz Basauri, G. M. (2022). Estadística Inferencial en la lógica de la investigación científica. Universidad Nacional Pedro Ruiz Gallo, Lambayeque.
Veiga, N., Otero, L., & Torres, J. (2020). Reflexiones sobre el uso de la estadística inferencial en investigación didáctica. InterCambios. Dilemas y transiciones de la Educación Superior, 7(2), 97-105. https://doi.org/10.29156/INTER.7.2.10
© 2025 Revista Multi-Ensayos.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.