ISSN 2410-5708 / e-ISSN 2313-7215
Year 11 | No. 30 | February - May 2022
© Copyright (2022). National Autonomous University of Nicaragua, Managua.
This document is under a Creative Commons
Attribution-NonCommercial-NoDerivs 4.0 International licence.
What mistakes do Primary Education students make in solving additive verbal enunciation problems?
https://doi.org/10.5377/rtu.v11i30.13393
Submitted on April 26, 2021 / Accepted on September 20, 2021
Ph.D. Jony Alexander Rojas Rojas
Doctor of Science with Orientation in Applied Mathematics
National Autonomous University of Nicaragua, Managua
Faculty of Education and Languages
https://orcid.org/0000-0003-4428-5127
B.A. Keneth Jovan Sotelo Sánchez
Teacher of Secondary Education in Mathematics
Section: Education
Scientific Articles
Keywords: education, error, mathematics, problems, fractions.
Abstract
In mathematics education for primary, a mistake is a teaching opportunity for the teacher, since realizing that the students have not reached the correct solution of the problem, he will then be able to design strategies that allow the students to overcome the error. However, this is possible only if the error has already been described. This paper describes the errors made by undergraduate students during work with additive problems of verbal enunciation on fractions. A total of 14 types of errors were found in the grouping problems, of these 13 are committed in aggregation problems.
INTRODUCTION
How concepts and problem-solving involving fractions are taught is one of the most difficult tasks for Mathematics teachers who address this content in primary education, because, according to Morales (2014), “the fractionation of the unit is prioritized or focuses on the mechanization of algorithms, that leave aside the reasoning and understanding of the concept that would allow the approach and solution of different mathematical problems”.
In some sectors, it is considered that learning to solve problems is learning to learn and that the most convenient approach concerning achieving this goal in teaching and learning environments is problem-based learning (Tandogan, & Orhan, 2007) cited by Gonzales and Maz (2018). Nicaragua’s own fifth-grade primary education curriculum establishes it as one of the competencies that every student must develop.
However, problems involving some application of school mathematics are left for the end of a unit or the end of the program, so most of the time students learn formal and abstract mathematics out of context. This fact was pointed out by Morales (2014), who states that these problems are usually omitted due to lack of time. This leads to problem-solving competence not being developed by students.
In Nicaraguan educational context, this phenomenon manifests itself because it is prioritized to comply with the programming of the contents in a set time. Therefore, the interest of this article is to identify the errors made by a sample of fifth-grade students of primary education when solving additive problems of aggregation and grouping. To achieve this identification of errors, we applied a questionnaire, composed of 4 items, which evaluates aspects of procedural development, translation from natural language to arithmetic, and conceptual processes in the resolution of additive problems. The analysis is carried out from two methodologies: thorough analysis of the students’ productions and through descriptive statistics tools. This allowed us a classification of errors that are within those proposed in the literature and other errors that had not been classified.
METHODOLOGY
The present research, according to its approach, is mixed. Quantitative because it makes use of statistical tools for the treatment of data information through the categorization and description of the properties, characteristics, and profiles of people, groups, communities, processes, and objects or any other phenomenon that is submitted to the analysis (Hernández, Fernández, and Baptista, 2010). Qualitative since it is a systematic activity oriented to the in-depth understanding of educational and social phenomena (in our case the errors made by students of 5th grade in the resolution of additive problems of verbal statement with fractions), to the transformation of practices and socio-educational scenarios, to decision making and also towards the discovery and development of an organized body of knowledge (Bisquerra, 2009). As for its level, it is descriptive because it deals with the characterization of a fact, phenomenon, individual or group, to establish its structure or behavior (Fidias, 2012), in addition, it has as a primary point the identification of the errors committed by primary education students in the resolution of additive problems of verbal statement both of aggregation. As a group for Bisquerra (2009) prospective studies advance in the collection of data, while the facts are happening, then the research is transversal and prospective because the data collection was in a single period, specifically in the second semester of the 2020 school year, and all the information was collected, according to the criteria of the researcher and for the specific purposes of the research, after the planning of the research.
Objectives
1.Identify the mistakes made by students of 5th grade of Primary Education in the resolution of additive problems of verbal enunciation.
2.Identify the family of problems (aggregation or grouping) that generates the greatest number of errors in students during work with additive verbal statement problems.
Participants
The research involved 20 out of 37 students enrolled in the fifth grade C of Primary Education of the Public School Teacher Calixto Moya de Masatepe. The age of the participants ranges from 10 to 13 years, in addition, 8 of the participants were girls and the remaining 12 were boys. It was not necessary to apply any formula to calculate the sample size, since the fifth grade C was selected because it was accessed, and the final sample was 20 because they were the ones who attended a class regularly. Finally, it should be noted that the type of sampling used was the causal or accidental non-probabilistic sample, which is the one in which the researcher directly and intentionally selects the sample, mainly because it has easy access to it and is representative of the population (Gil, Rodríguez and García, 1995; Albert, 2006).
Tools
For the collection of the information, the survey was used as a technique and a questionnaire was used as an instrument, which consisted of 4 additive problems of the verbal statement, of which 2 were of grouping and 2 of aggregation. The first two problems involve fractions with equal denominators and the last two fractions with different denominators. The problems were excerpted from the fifth-grade textbook The Power of Mathematics, by Avendaño D. (2019). And then appropriate to the second cycle level of Nicaraguan primary education. This instrument was validated in terms of content and belonging by the full professor and the director of the Public School.
Regarding the analysis criteria for the identification of errors, the classification was taken that includes the set of all arithmetic errors in verbal problems (Table 1) proposed by Casajús (2005) and recently used in Del Rosal, Gutiérrez and Maz-Machado (2018) and Maz-Machado, González de Quevedo Herranz and Argudo-Osado (2018). In addition, all the errors evidenced in the productions of the students according to the aforementioned classification were collected and counted. When the approach was incorrect, it continued to be corrected to verify if there were errors in the execution of the operations. Similarly, in a correct approach, the analysis was not finished until all the errors committed were collected.
Table 1.
Error Code
|
Aspects to categorize |
|
Error-free problem |
|
Unanswered problem |
|
Incorrect problem (with incorrect approach) An error of leads. (E1) Incorrect translation of the data figure (change some figures for different ones). Alteration of the digits. (E2) Always subtract larger numbers except for the small ones (both in minuend and in Subtrahend). (E3) Although it clearly expresses the operation to be performed (addition or subtraction), it alters the two operations in its execution. (E4) It misplaces the members of the subtraction, whether or not there is success in the choice of the algorithm. (E5) Data digits are left or added to the statement. (E6) There are no errors in the execution of operations. (E7) In a trade, numbers are left unoperated. (E8) It expresses an operation and operates contrary to what is proposed. (E9) Use numbers in the letters of the statement as data. (E10) The incomplete problem for not expressing the solution explicitly. (E11) Operations are missing. (E12) Meaningless operation. (E13) Wrong problem (with correct approach) In a trade, numbers are left unoperated. (E14) Error in the carried. (E1) |
RESULTS
To report clearly and simply the findings of the research, we have divided this section into two parts: In the first, we report all the errors evidenced in the productions of the students during the work with the problems present in the instrument. In the second, we present the description of the distribution of the totality of the errors according to the type of error, the family of problems (grouping or aggregation), and the sex.
Errors evidenced in the productions of the students.
Of the 15 errors present in the classification of Casajús (2005) only 4 of them were obtained: Always subtract the largest numbers except for the small ones (E3), there are no errors in the execution of the operations (E7), incomplete problem for not expressing the solution explicitly (E11), Meaningless operation (E8). In addition, 10 errors were identified that do not belong to the Classification of Casajús, namely Incorrect production of data to an arithmetic language (D1), Does not respect the problem-solving structure (D2), Invents data (D3), Operates only the numerators (D4), Applies contrary operation (D5), incomplete simplification (D6), Sin simplify (D7), Simplify inadequately (D8), Incorrectly applies the algorithm of the sum of fractions with different denominator is (D9), Writes as a response data of the statement (D10); of these D6 and D9 belong to a classification present in Gonzales (2015), the error D1 appears raised in Morales (2014) as a possible difficulty of students when solving a verbal problem, the other errors constitute the first finding of this work.
Below, we present two examples that show the mistakes made by students in solving additive problems on fractions.
There are no errors in the execution of operations (E7).
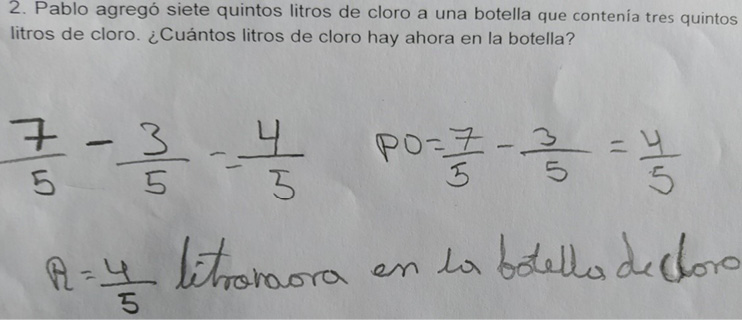
Paul added seven-fifths liters of chlorine to a bottle containing three-fifths liters of chlorine. How many liters of chlorine are now in the bottle? (Literal translation of the Math problem)
(Figura 1) Liter now in the bottle of chlorine (Literal translation of a student's response).
We can observe that the student incorrectly poses the data of the problem by not correctly identifying the operation that was required to be applied, however, he correctly executes the proposed subtraction.
It does not respect the problem-solving structure (D2).

Paul added seven-fifths liters of chlorine to a bottle containing three-fifths liters of chlorine. How many liters of chlorine are now in the bottle? (Literal translation of the Math problem)
(Figura 2) PO: 5/1 liter is in Paul's bottle (literal translation of another student's response).
Regarding the problem-solving structure, we can observe that the student does not write data, the operations approach is named as Re and the answer as Po. This can be attributed to the little learning acquired about the problem-solving structure.
Total distribution of errors
Once we have identified the mistakes that students make during work with additive problems of verbal statements involving fractions, it is interesting to know how frequent these errors are, which will allow us to infer about their persistence.
In total it was found that 100% of the problems present at least one error in their resolution. In addition, all the problems were worked on by the students, which indicates that they had ideas and/or strategies to address the problems.
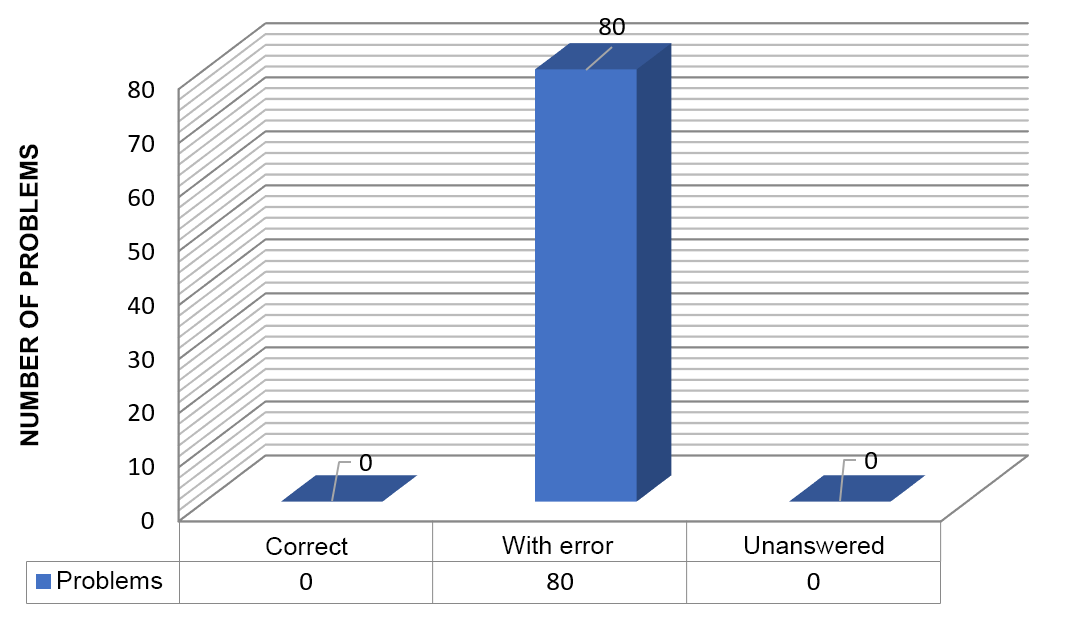
Graphic 1.
Frequency of problems according to student responses.
When taking into account the frequency with which each of the errors evidenced occur, it must be that globally of the 15 types of errors considered in the classification of Casajús (2005), 4 of them are present in the productions of the students. Of these, the most frequent is E7 with a percentage of 7.11% of the total. Of the errors that are not considered by Casajús the most frequent are: D1, D2, and D9 with a percentage of 14.13%, 30.04%, and 12.25%, respectively.
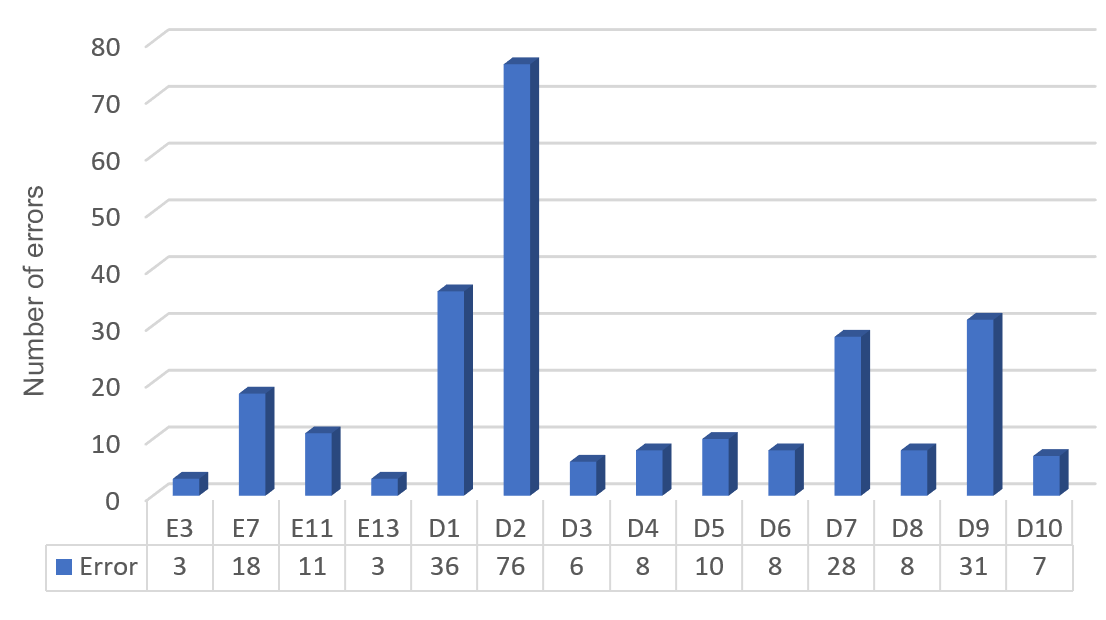
Graphic 2.
Frequency of errors present in the study.
According to the family of problems, for the aggregation family, 13 types of errors were committed of the 14 identified, being the most frequent: It does not respect the problem-solving structure (D2), without simplifying (D7), Incorrect translation of data into an arithmetic language (D1)and Incorrectly applies the algorithm of the sum of fractions with different denominator is (D9).
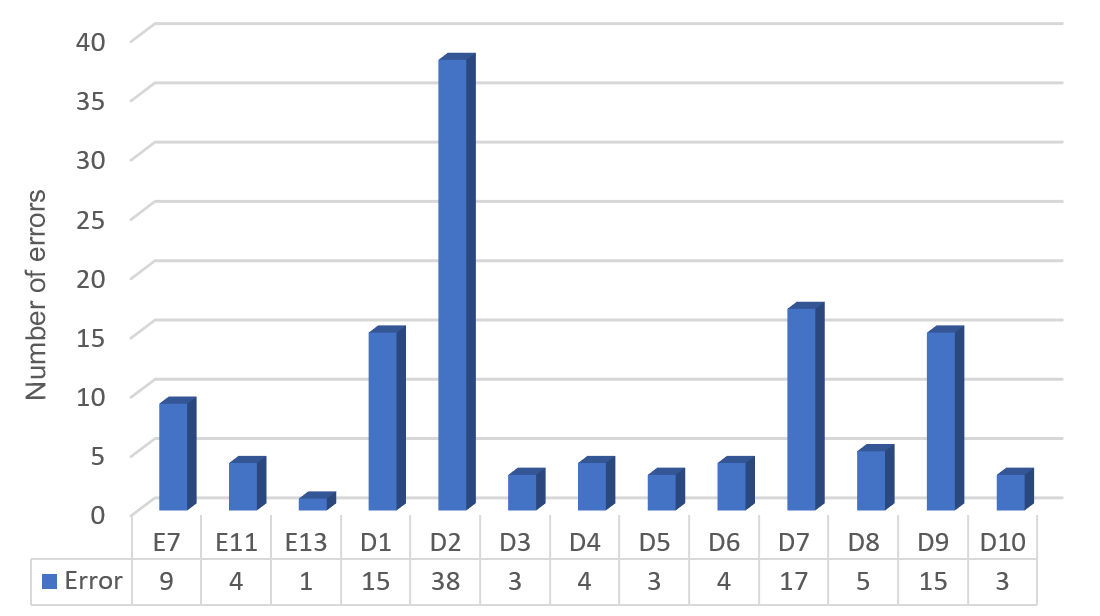
Graphic 3.
Frequency of errors present in aggregation problems.
In the problems of the grouping family, the 14 errors were identified, the most frequent being: It does not respect the problem-solving structure (D2), Incorrect translation of data into an arithmetic language (D1), and incorrectly applies the algorithm of the sum of fractions with different denominator (D9).
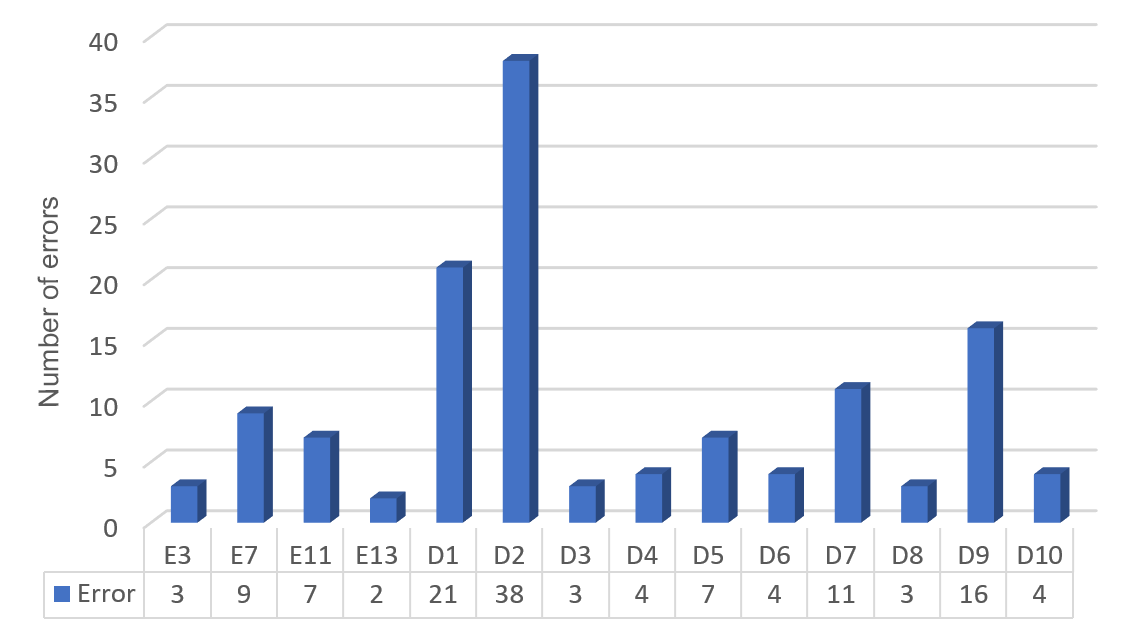
Graphic 4.
Frequency of errors present in grouping problems.
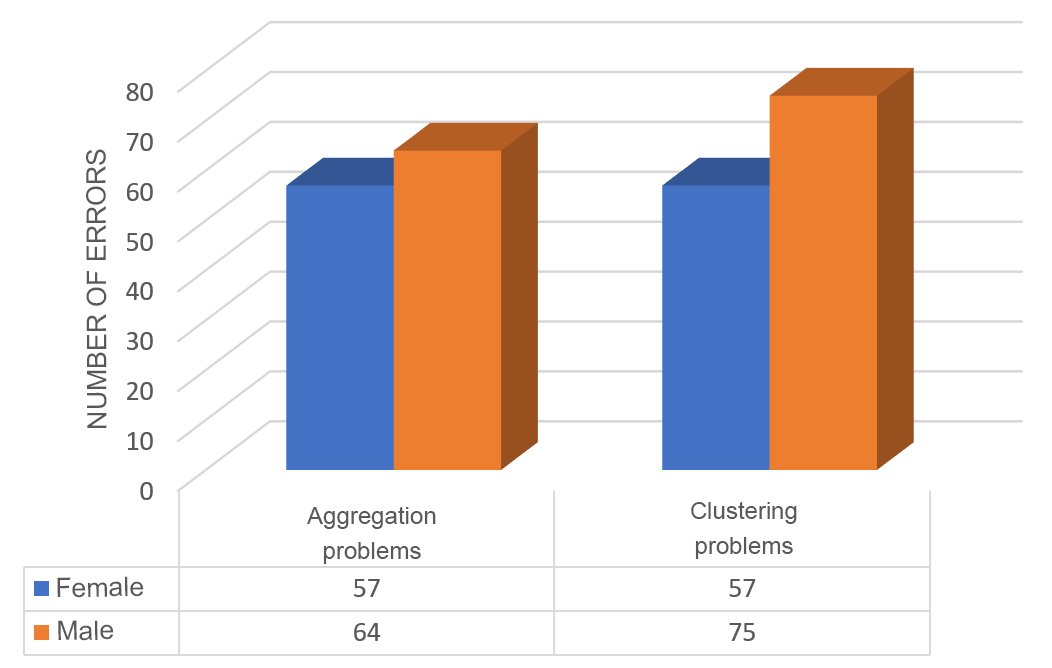
When reviewing the errors by a family of problems and by sex it is obtained that men made more mistakes than women, with percentages of 54.94% and 45.06%, respectively. In addition, for women, both families generate the same difficulty, while men make more mistakes in the grouping family, which means that it generates greater difficulty.
CONCLUSIONS
After having carried out the research process, with the data obtained, we can confirm that students present difficulties in the correct interpretation of the statement of a problem and when operating fractions of different denominators.
It was possible to identify that the most mistakes committed by students were: do not respect the problem-solving structure (D2), Incorrect translation of data into an arithmetic language (D1), and incorrectly applying the algorithm in the sum of fractions of the different denominator is (D9 ), which represent 30.04%, 14.13% and 12.25% of the total errors made in the study, respectively. It is important to note that none of the students tried to find equivalent fractions to add fractions of different denominators, this means that they do not know or do not master the algorithm of the sum of fractions via fraction enlargement.
The data obtained show that more errors were made in the grouping problems (52.17%), however, the percentages of errors made in each family of problems concerning the total of errors made in the study, are similar.
In the Nicaraguan context, the classification of Casajús (2005) is insufficient to make a classification of errors in primary education on fractions, so we propose as future work the design and validation of an instrument that allows identifying the errors that students commit during their productions in the resolution of additive problems of verbal statements that involve fractions.
In addition, it is evident that students, although they have ideas to solve problems, these present inconsistency and fail to concretize it due to failures in operations with fractions and little practice in the translation of the verbal problem into arithmetic language.
References
Albert, M. (2006). Educational research. Theoretical Keys. Madrid: McGraw-Hill.
Bisquerra, R. (2009). Methodology of educational research. Madrid: The Wall.
Del Rosal, A., et al (2018). Errors in the resolution of arithmetic problems of change and combination in students of 2nd grade of primary school.
Phidias, G. (2012). The research project: Introduction to scientific methodology (ed.). Bolivarian Republic of Venezuela: EDITORIAL EPISTEME, C.A.
Gonzales, D. (2015). Common mistakes in the learning of fractions: A study with students of 12/13 years in Cantabria.
Gonzales, M., Maz, A. (2018). Analysis of errors in solving additive problems of verbal enunciation in primary education.
Gil, J., Rodriguez, G., and Garcia, E. (1995). Basic statistics are applied to the sciences of education. Seville: Kronos.
Hernández, R., Fernández, C., & Baptista, M. (2010). Research methodology. Mexico: McGra-Hill.
León, C., Maz, A., Madrid, M., Casas, J. (2013). Student-to-teacher mistakes when working with fractions.
Morales, R. (2014). Difficulties and errors in solving problems with rational numbers.
Rodríguez, C., Navarro, C., Castro, A., García, M. (2019) Semantic structures of additive problems of verbal enunciation in Mexican textbooks.
Salgado, J., et al, (2019), Mathematics 5th grade,Managua, Nicaragua, MINED.
Zubieta, J. (2018). Typification of errors and difficulties in the development of trigonometric functions of tenth-grade students.