Palabras Clave: Función costo, Derivadas parciales, Ciencias económicas, Producción y resolución de problemas.

RESUMEN

El presente artículo de investigación tiene como título “Aplicaciones de las derivadas parciales en las ciencias económicas: Función de costo y producción”, el cual consiste en una serie de situaciones con sus respectivas soluciones aplicables en el área de las ciencias económicas y empresariales. El objetivo de este estudio es disponer de una guía de problemas con sus respectivas soluciones mediante derivadas parciales aplicadas en el área de Administración y Economía. Se utilizó un análisis descriptivo y un enfoque mixto con predominancia cualitativa, proporcionando una mejor adquisición de las ciencias exactas puesto que se tomaron aspectos relevantes de diferentes fuentes de información confiables. Por medio de este estudio se logró obtener resultados de calidad que ayuden a fomentar e incrementar los conocimientos tanto de estudiantes como también docentes que puedan acceder a este estudio y esto contribuye al desarrollo del aprendizaje significativo en materia de ciencias económicas y administrativas, puesto que toma los aspectos de innovación en la resolución de problemas y además permite fortalecer el pensamiento crítico.

Abstract

This research article is entitled “Applications of partial derivatives in economics: Cost and production function”, which consists of a series of situations with their respective solutions applicable in the area of economics and business. The objective of this study is to have a guide of problems with their respective solutions by means of partial derivatives applied in the area of Administration and Economics. A descriptive analysis and a mixed approach with a qualitative predominance were used, providing a better acquisition of the exact sciences since relevant aspects were taken from different reliable sources of information. Through this study it was possible to obtain quality results that help to promote and increase the knowledge of both students and teachers who can access this study and this contributes to the development of meaningful learning in economic and administrative sciences, since it takes the aspects of innovation in problem solving and also allows to strengthen critical thinking.

Keywords: Cost function, Partial derivatives, Economics, Production and problem solving.

1. INTRODUCCIÓN

En la época actual existen un sin número de aplicaciones de las matemáticas y en su aspecto general relacionadas con otras ciencias como la economía, la medicina, la ingeniería, la física, entre otras, las cuales hacen de la matemática una ciencia primordial para el desarrollo de modelos que resuelvan una situación del contexto social o ya sea de la índole que se trate.

Sustentando lo expresado anteriormente por medio de Moriana (2003), que argumenta que “es universalmente aceptada la idea de que las matemáticas constituyen el lenguaje de las ciencias. En la medida que una rama del conocimiento humano se desarrolla, se va estructurando, adopta el lenguaje preciso de las matemáticas” (p. 12). En contraste con lo que plantea Herrera Castrillo (2023), “las matemáticas siempre han sido vistas aisladas de otras ciencias, pero en realidad esta guarda mucha relación con otros ámbitos” (p. 32).

Por lo antes planteado y tomando en cuenta la relación de la matemática con otras ciencias, el desarrollo de este trabajo se basa en aplicaciones de las derivadas parciales (perteneciente al cálculo diferencial) en las ciencias económicas como una propuesta basada en la resolución de problemas, es decir se presentan un sinnúmero de situaciones problemáticas que se aplican en el área económica.

Se considera el concepto de modelo económico en sentido amplio, como una representación simplificada mediante una formulación matemática de un cierto conjunto de relaciones económicas (Sampedro J. L. 1959, citado en Moriana, 2003, p 102). Es decir, los modelos han de tratar de representar un fenómeno económico real mediante un conjunto de relaciones y lo han de hacer en términos matemáticos.

Es de gran relevancia señalar que las aplicaciones propuestas son tomadas de distintas revisiones bibliográficas realizadas, algunas que ya estaban resueltas se desarrollaron de una manera más sencilla y detallada, pero en su mayoría son de los problemas propuestos en los libros de texto de matemática para administración y economía los cuales detallamos en la bibliografía de dicho trabajo.

La resolución de problemas constituye el eje fundamental de cualquier proceso y especialmente donde se encuentre involucrada la Matemática o, en su defecto, cualquier ciencia que dependa directa o indirectamente de la misma. Brousseau (1983), en su Teoría de las situaciones didácticas atribuye un lugar preferencial a la resolución de problemas como base fundamental del conocimiento. De acuerdo a la relación de la matemática con las ciencias económicas porque nos lleva a la aplicación de modelos matemáticos que permitan darle solución a diversas situaciones económicas y por tal razón, la presente investigación se fundamenta en la resolución de problemas de derivadas parciales involucrando ambas ciencias.

De acuerdo a revisiones bibliográficas, existen grandes cantidades de publicaciones y estudios que tratan del papel que cumplen las matemática en las ciencias económicas. Este tema, no exento de polémica, y además de repercutir en el desarrollo de la Economía como ciencia social, influye decisivamente en el desarrollo de los profesionales e involucrados en los procesos económicos.

Son cada vez más los economistas y administradores que consideran que la utilización de las matemáticas como lenguaje simbólico y método de razonamiento científico constituye un elemento de ayuda inestimable en las tareas y objetivos de dichas ciencias. Su presencia resulta fundamental tanto en la descripción de las complejas relaciones económicas como en la formulación de proposiciones sobre relaciones de comportamiento.

De tal modo, la contribución de la Matemática a las Ciencias Económicas no puede verse de manera aislada sino como una consecuencia de la evolución histórica de ambas y de sus relaciones con otros campos como la Física, Biología, Ecología, Medicina, Astronomía, entre otros.

2. MÉTODOS

2.1. Tipo de Estudio

Esta investigación, según su enfoque, es de tipo mixta, ya que hace énfasis en la descripción y analisis de problemas referente al ambito economico y administativo para inferir y afinar preguntas de investigación en el proceso de interpretación, además se aplica la lógica inductiva de lo particular a lo general. Por ende, posee el carácter cuantitativo y cualitativo.

Según Hernández et al. (2014), “la meta de la investigación mixta no es reemplazar a la investigación cuantitativa ni a la investigación cualitativa, sino utilizar las fortalezas de ambos tipos de indagación combinándolas y tratando de minimizar sus debilidades potenciales” (p. 532).

Cabe destacar que, el enfoque de mayor predominio y presencia es el cualitativo, es decir que, durante el proceso investigativo se describe y analizan problemas de aplicación sobre función de costos.

De este modo, Taylor y Bodgan (2001), afirman que:

La investigación cualitativa produce datos descriptivos: las propias palabras de las personas, habladas o escritas, y la conducta observable. Es decir, este enfoque puede concebirse como un conjunto de prácticas interpretativas que hacen al mundo visible, lo transforman y convierten en una serie de representaciones en forma de observaciones, anotaciones, grabaciones y documentos. (p. 20).

Recolección de la Información

Hernández y Duana (2020), explican que:

La recolección de datos es considerada como la medición y es una precondición para obtener el conocimiento científico. El instrumento de recolección de datos está orientado a crear las condiciones para la medición. Los datos son conceptos que expresan una abstracción del mundo real, de lo sensorial, susceptible de ser percibido por los sentidos de manera directa o indirecta, donde todo lo empírico es medible, (p.51).

Es decir, que la recolección de información es aquella que proporciona la explicación de una temática importante para el desarrollo del conocimiento, por ejemplo, en esta investigación se tomaron diferentes fuentes de información para recolectar datos adecuados al contenido tales como: revistas, libros, sitios web, PDF, entre otros.

En este estudio se dio un análisis descriptivo para llegar a la interpretación de los datos obtenidos mediante las diferentes fuentes de información, iniciando con la codificación de los datos recabados para que resultara más fácil su comprensión, la que se elaboró mediante resumen, imágenes, notas al pie y tomando en cuenta el análisis cualitativo y cuantitativo de los problemas de función de costo y producción.

3. ANÁLISIS Y DISCUSIÓN DE RESULTADOS

En este apartado se presentan una serie de problemas aplicados a costo y producción, solucionándolos por medio de las definiciones y propiedades básicas de las derivadas parciales, y para comprender mejor se presenta la definición básica de costo y producción, posteriormente los problemas de aplicación a estos dos términos.

Costo: De acuerdo a (Bravo, 2014, citado en Cando, 2020), los costos son:

Los desembolsos que realiza la empresa para la fabricación o elaboración de un producto o la prestación de un servicio, el costo constituye una inversión, es recuperable, trae consigo ganancia, es un concepto que tiene vigencia en la empresa industrial. El costo de los productos fabricados está dado por los costos de producción en que fue necesario incurrir para su fabricación. El costo constituye la base para el costeo de productos, la evaluación del desempeño y la toma de decisiones gerenciales. El costo se define como el “valor” sacrificado para obtener bienes y servicio, (pp. 21-22).

Producción: Según Valhondo y Sáez, (2014), la producción consiste en:

Una secuencia de operaciones que transforman los materiales haciendo que pasen de una forma dada a otra forma que se desea obtener. También se entiende por producción la adición de valor a un bien o servicio, por efectos de una transformación. Producir es extraer, modificar los bienes con el objeto para volverlos aptos para satisfacer las necesidades. (pp. 19-21)

De manera general se puede concluir que las empresas son las encargadas de la producción, es decir de los bienes y servicios que se ofrecen en el mercado, considerando no solamente la producción de bienes físicos (alimentos, vestidos, automóviles, entre otros), sino también la prestación de servicios (comercialización, sanidad, enseñanza, transportes, investigaciones entre otras).

Problemas de Aplicación

1. Se construye una caja rectangular cerrada de manera que su volumen sea 36 pies cúbicos. El costo del material de la tapa y de la base es de $10 el pie cuadrado, el del material para las partes de enfrente y de atrás es de $9 el pie cuadrado y el material para los otros lados es de $7 el pie cuadrado.

a. Determine la función de costo , donde son las medidas del largo y el ancho de la base de la caja respectivamente.

b. Calcule e intérprete los resultados.

Figura 1. Representación del primer problema

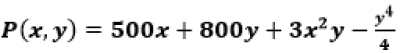
Creación Propia

Solución:

a. Determinar la función de costo de la función

Tomando en cuenta que el volumen de un rectángulo está dado por:

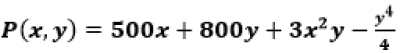
De acuerdo a los datos brindados por el problema, el costo del material para construir la caja es

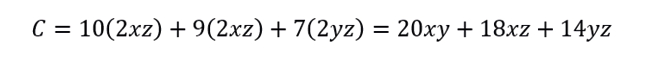
Al reemplazar la expresión de en el costo , se obtiene

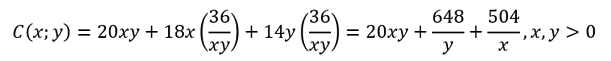
b. Las derivadas parciales de con respecto a son

Luego

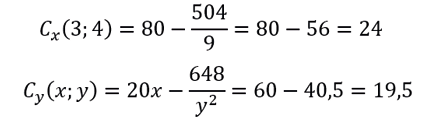
Interpretación de los resultados

Por tanto, cuando el lado de la base de la caja de medida es 3 pies y el lado de medida se mantiene constante en 4 pies, el costo de construcción de la caja aumenta a una razón de $24 por cada pie de aumento en .

De manera similar, cuando el lado de la base de medida es 4 pies y el lado de medida se mantiene constante en 3 pies, el costo de construcción aumenta a una razón de $19,5 por cada pie de aumento en .

2. Una compañía que fabrica computadoras ha determinado que su función de producción está dada por 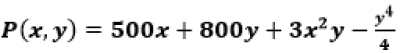, donde es el tamaño de la fuerza de trabajo (en horas de trabajo por semana) e es la cantidad de capital (en unidades de $1000) invertido.

a. Encuentre Px (x,y) y Py (x,y) cuando x=50 e y= 20 e intérprete los resultados.

Solución:

Sea x=el tamaño de la fuerza de trabajo (en horas de trabajo por semana)

y=la cantidad de capital (en unidades de $1000) invertido.

Derivando parcialmente respecto a en la función de producción tenemos:

Derivar parcialmente respecto a la variable y respecto a la variable en la función de producción:

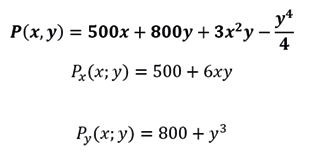
Sustituyendo x=50 e y= 20 en Px (x;y) y Py (x;y)

Px (50;20)=500+6(50)(20)

Px (50;20)=500+6000

Px (50;20)=6 500

Py (50;20)=800+(20)3

Py (50;20)=800+8000

Py (50;20)=8 800

Interpretación de los resultados: En conclusión, cuando el tamaño de la fuerza de trabajo equivale a 50 horas de trabajo por semana y, el capital invertido se mantiene fijo en 20 (unidades de $1000) la producción de computadoras aumenta en 6500 unidades producidas.

De manera similar, cuando el capital invertido es de 20 (unidades de $1000) y tamaño de la fuerza de trabajo se mantiene fija en 50 horas de trabajo por semana la producción de computadoras aumenta a 8800 unidades producidas.

3. El costo (en dólares) de una pequeña compañía de muebles por fabricar una Unidad de varios artículos distinto de maderas está dado por:

C(x;y)=5+5x+22y

Donde x representa el número de píes de tablas utilizados y
expresa el número de horas de trabajo necesarias para ensamblado y acabado. Si para hacer un librero se necesitan 20 pies de tabla y 2.5 horas de trabajo, encuentre el costo de fabricación.

Solución:

Sea x el número de píes de tablas utilizados

Sea y el número de horas de trabajo necesarias para ensamblado y acabado

para resolver dicha situación solo necesitamos sustituir x=20 e y =2,5 en la función original.

C(x;y)=5+5x+22y

C(20;2,5)=5+5(20)+22(2,5)

C(20;2,5)=5+100+22(2,5)

C(20;2,5)=5+100+55

C(20;2,5)=160 dólares

4. Suponga que la producción de Q unidades del producto de una compañía se determina mediante la función de producción de Cobb-Douglas

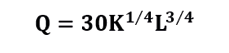
Donde K representa la inversión de capital en dólares y L las horas de trabajo

a. Encuentre Q si K=10 000 dólares y L=625 horas.

Remplazando tenemos:

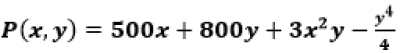
Convirtiendo las potencias en raíces se logra lo siguiente:

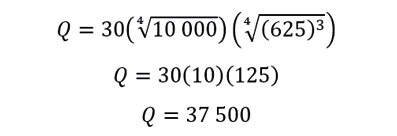
R// Cuando el capital invertido es 10 000 dólares y se trabajan 625 horas, las unidades producidas serán 37 500.

b. ¿Qué pasa sí la inversión y las horas trabajadas se reducen a la mitad? Entonces K=5 000 dólares y L=312,5 horas.

Remplazando tenemos:

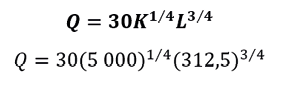
Convirtiendo las potencias en raíces se logra lo siguiente:

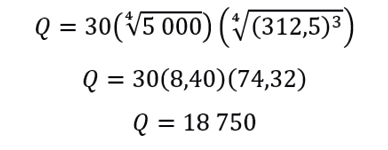
Respuesta: Cuando el capital invertido y las horas trabajadas se reducen a la mitad la producción también se reduce a la mitad.

c. Si se mantiene la inversión de capital en 10 000 dólares, trace la gráfica de Q como función de L.

La ecuación sería:

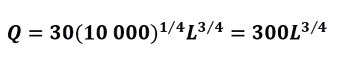
Figura 2. Gráfica de Q en función de L

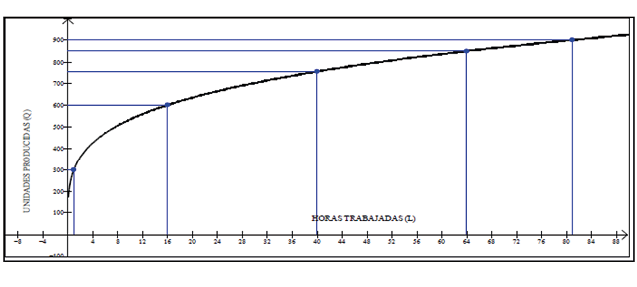
Creación Propia

5. Una pastelería produce chocolates blancos y chocolate oscuro. El costo de material y mano de obra por producir un kilo de chocolate blanco es de 6 dólares y los oscuros 5 dólares. Suponga que la empresa tiene costos fijos semanales de 1200 dólares.

a. Encuentre el costo semanal como función de la cantidad de kilos de chocolates de cada tipo producido a la semana.

b. Suponga que la pastelería vende el kilo de chocolate blanco a 10 dólares y el oscuro a 8 dólares. Obtenga la función de utilidad mensual como función del número de kilos de cada tipo producidas y vendidas a la semana.

Solución:

a. El costo de material y manos de obra por producir q1 kilos de chocolate blanco y kilos de chocolate oscuro están dado por y respectivamente.

El costo conjunto en este caso está dado por 6q1 y 5q2 respectivamente.

C(q1,q2) = costo fijo + costo variable

C(q1,q2) = 1 200+(6q1+5q2)

b. Primero obtendremos la función de ingreso conjunto es claro que

q1=kilos de chocolate blanco

q2=kilos de chocolate oscuro

I(q1,q2) = Ingreso por la venta de q1 + Ingreso por la venta de q2

I(q1,q2)=10q1+8q2

Finalmente tenemos que

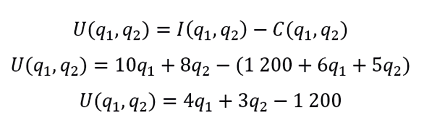
6. La función de producción de una empresa es P(l,k)=450l3⁄5 k2⁄5 donde es la producción que se obtiene cuando se emplean I unidades de mano de obra y k unidades de capital. Si en un momento dado se ocupan 243 unidades de mano de obra y 32 de capital.

a. Aproxime el efecto en la producción de incrementar la mano de obra a 248 unidades y disminuir el capital a 31 unidades monetarias.

b. Calcular el cambio porcentual en la producción.

Solución:

a.Si representamos el cambio de la producción como dt, y el incremento en la mano de obra y el capital como dl y dk, respectivamente tendremos la ecuación

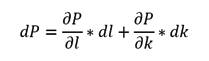
Las derivadas parciales son:

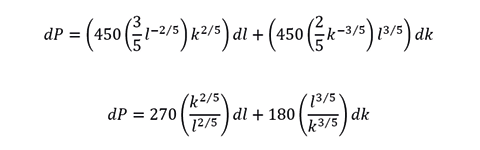
Si tenemos que l=243, k=32 entonces:

dl = 248 - 243 = 5 y dk = 31 - 32 = -1

Sustituyendo los valores en

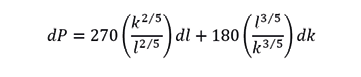
Tenemos

Respuesta: De esta manera la producción disminuye aproximadamente en 7,5 unidades.

b. El cambio porcentual de la producción es

Respuesta: La producción cae en un 0,015%.

4. CONCLUSIONES

Se revisaron los aspectos teóricos y prácticos sobre las distintas aplicaciones de las derivadas parciales en las ciencias económicas basadas en la resolución de problemas.

Tomando en cuenta los fundamentos teóricos se realizó una breve reseña histórica de las matemáticas en relación con las ciencias económicas resaltando la importancia y su aplicabilidad en dicha área del conocimiento.

Además, se tomaron en cuenta los aspectos generales de las derivadas parciales como la definición, notación y los distintos tipos que existen como fundamento básico para la resolución de problemas.

Se analizaron en su forma general las distintas aplicaciones de las derivadas parciales y su relación con las ciencias económicas tomando en cuenta distintas bibliografías de las cuales se tomaron situaciones resueltas y en su mayoría propuestas.

Se proponen una serie de problemas con sus respectivas soluciones detalladas y análisis de las respuestas, entre las cuales sobre salen problemas de costo y producción.