ISSN 2410-5708 / e-ISSN 2313-7215
Year 13 | No. 37 | June - September 2024
© Copyright (2024). National Autonomous University of Nicaragua, Managua.
This document is under a Creative Commons
Attribution-NonCommercial-NoDerivs 4.0 International licence.
Applications of partial derivatives in economics: cost and production function
https://doi.org/10.5377/rtu.v13i37.18131
Submitted on June 01, 2023 / Accepted on May 23rd, 2024
Norman Rafael López Sánchez
B.S. in Educational Sciences with a major in Mathematical Physics
National Autonomous University of Nicaragua, Managua. Regional Multidisciplinary Faculty of Esteli
Cliffor Jerry Herrera Castrillo
PhD in Applied Mathematics
National Autonomous University of Nicaragua, Managua. Regional Multidisciplinary Faculty of Esteli
Section: Social sciences, Business education and Law
Scientific research article
Keywords: Cost function, partial derivatives, economic sciences, production, and problem solving
ABSTRACT
This research article is entitled “Applications of partial derivatives in economics: Cost and production function”, which consists of a series of situations with their respective solutions applicable in the area of economics and business. The objective of this study is to have a guide of problems with their respective solutions using partial derivatives applied in the area of Administration and Economics. A descriptive analysis and a mixed approach with a qualitative predominance were used, providing a better acquisition of the exact sciences since relevant aspects were taken from different reliable sources of information. Through this study, it was possible to obtain quality results that help to promote and increase the knowledge of both students and teachers who can access this study and this contributes to the development of meaningful learning in economic and administrative sciences since it takes the aspects of innovation in problem-solving and also allows to strengthen critical thinking.
1. INTRODUCTION
In the present time, there are a great number of applications of mathematics and in its general aspect related to other sciences such as economics, medicine, engineering, and physics, among others, which make mathematics a primordial science for the development of models that solve a situation of the social context or whatever it may be.
This is supported by Moriana (2003), who argues that “it is universally accepted that mathematics is the language of the sciences. As a branch of human knowledge develops and becomes structured, it adopts the precise language of mathematics” (p. 12). In contrast to what Herrera Castrillo (2023) states, “Mathematics has always been seen in isolation from other sciences, but in reality it is closely related to other fields” (p. 32).
Given the above and taking into account the relationship of mathematics with other sciences, the development of this work is based on applications of partial derivatives (belonging to differential calculus) in the economic sciences as a proposal based on problem-solving, i.e. several problematic situations are presented that are applied in the economic area.
The concept of the economic model is considered in a broad sense, as a simplified representation utilizing a mathematical formulation of a certain set of economic relations (Sampedro J. L. 1959, cited in Moriana, 2003, p 102). In other words, models must try to represent a real economic phenomenon utilizing a set of relationships and they must do so in mathematical terms.
It is of great relevance to point out that the proposed applications are taken from different bibliographic reviews, some that were already solved were developed in a simpler and more detailed way, but most of them are from the problems proposed in the textbooks of mathematics for administration and economics, which are detailed in the bibliography of this work.
Problem-solving constitutes the fundamental axis of any process, especially where mathematics is involved or, failing that, any science that depends directly or indirectly on it. Brousseau (1983), in his Theory of didactic situations, attributes a preferential place to problem solving as the fundamental basis of knowledge. According to the relationship of mathematics with economic sciences, it leads us to the application of mathematical models that allow us to give solutions to diverse economic situations and for this reason, the present research is based on the resolution of partial derivatives problems involving both sciences.
According to bibliographic reviews, there are a large number of publications and studies dealing with the role of mathematics in the economic sciences. This topic is not exempt from controversy, and besides having repercussions on the development of economics as a social science, has a decisive influence on the development of professionals and those involved in economic processes.
More and more economists and administrators consider that the use of mathematics as a symbolic language and method of scientific reasoning is an invaluable aid in the tasks and objectives of these sciences. Its presence is fundamental both in the description of complex economic relationships and in the formulation of propositions about behavioral relationships.
Thus, the contribution of mathematics to the economic sciences cannot be seen in isolation but as a consequence of the historical evolution of both and of its relations with other fields such as physics, biology, ecology, medicine, and astronomy, among others.
2. METHODS
2.1. Type of Study
This research, according to its approach, is of a mixed type, since it emphasizes the description and analysis of problems related to the economic and administrative environment to infer and refine research questions in the process of interpretation, in addition to applying the inductive logic from the particular to the general. Therefore, it has a quantitative and qualitative character.
According to Hernández et al. (2014), “the goal of mixed research is not to replace quantitative research or qualitative research, but to use the strengths of both types of inquiry by combining them and trying to minimize their potential weaknesses” (p. 532).
It should be noted that the most predominant approach is the qualitative one, i.e., during the research process, application problems on cost function are described and analyzed.
Thus, Taylor and Bodgan (2001) state that:
Qualitative research produces descriptive data: people’s own words, spoken or written, and observable behavior. In other words, this approach can be conceived as a set of interpretive practices that make the world visible, transform it, and convert it into a series of representations in the form of observations, notes, recordings, and documents (p. 20).
2.2. Information Collection
Hernández and Duana (2020), explain that:
Data collection is considered a measurement and is a precondition for obtaining scientific knowledge. The data collection instrument is oriented to create the conditions for measurement. Data are concepts that express an abstraction of the real world, of the sensory, susceptible to be perceived by the senses directly or indirectly, where everything empirical is measurable, (p.51).
That is, the collection of information is that which explains an important subject for the development of knowledge, for example, in this research different sources of information were taken to collect data appropriate to the content such as magazines, books, websites, and PDF, among others.
In this study, a descriptive analysis was made to arrive at the interpretation of the data obtained through the different sources of information, starting with the codification of the data collected to make it easier to understand, which was elaborated using a summary, images, footnotes and taking into account the qualitative and quantitative analysis of the cost and production function problems.
3. ANALYSIS AND DISCUSSION OF RESULTS
In this section a series of problems applied to cost and production are presented, solving them using the definitions and basic properties of the partial derivatives, to better understand the basic definition of cost and production, later the problems of application to these two terms are presented.
Cost: According to (Bravo, 2014, cited in Cando, 2020), costs are:
The disbursements made by the company for the manufacture or elaboration of a product or the provision of a service, the cost constitutes an investment, is recoverable, brings profit, is a concept that is valid in the industrial company. The cost of the manufactured products is given by the production costs incurred for their manufacture. Cost is the basis for product costing, performance evaluation, and management decision-making. Cost is defined as the “value” sacrificed to obtain goods and services (pp. 21-22).
Production: According to Valhondo and Sáez, (2014), production consists of:
A sequence of operations that transform materials causing them to pass from a given form to another form that is desired to be obtained. Production is also understood as the addition of value to a good or service, through the effects of a transformation. To produce is to extract, to modify goods to make them suitable to satisfy needs (pp. 19-21).
Generally speaking, it can be concluded that companies are in charge of production, that is, of the goods and services offered in the market, considering not only the production of physical goods (food, clothing, automobiles, among others) but also the provision of services (marketing, health, education, transportation, research, among others).
APPLICATION PROBLEMS
1.A closed rectangular box is constructed so that its volume is 36 cubic feet. The cost of the material for the lid and base is $10 per square foot, the material for the front and back sides is $9 per square foot, and the material for the other sides is $7 per square foot.
a.Determine the cost function C(x; y), where x and y are the measures of the length and width of the base of the box respectively.
b.Calculate Cx (3; 4) and Cy( 3;4) and interpret the results.
Figure 1.
Representation of the first problem
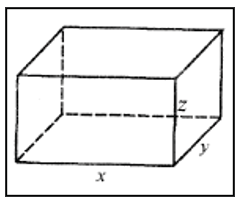
Own creation
Solution:
a.Determine the cost function of the function
Taking into account that the volume of a rectangle is given by:
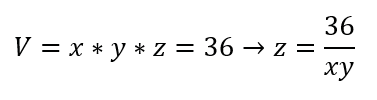
According to the data given by the problem, the cost of the material to build the box is
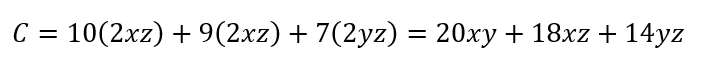
By replacing the expression for z in the cost C, we obtain
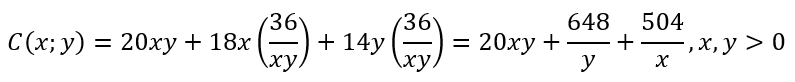
b.The partial derivatives of C concerning x and y are
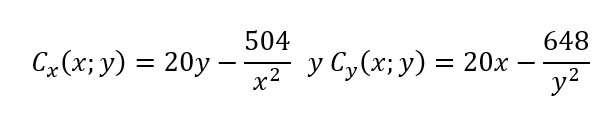
Then
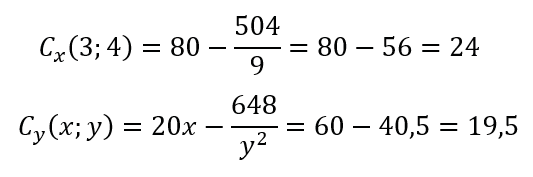
Interpretation of the results
Thus, when the base side of the box measuring x is 3 ft and the side measuring y is held constant at 4 ft, the cost of building the box increases at a rate of $24 per foot increase in x.
Similarly, when the base side of measurement y is 4 feet and the side of measurement x is held constant at 3 feet, the construction cost increases at a rate of $19.5 for each foot of increase in y.
2.A company that manufactures computers has determined that its production function is given by P(x, y) = 500x + 800y + 3x2y - y4/4 where x is the size of the labor force (in labor hours per week) and y is the amount of capital (in units of $1000) invested.
a.Find Px (x, y) y Py (x, y) when x=50 and y=20 and interpret the results.
Solution:
Let x = the size of the labor force (in hours of work per week).
y = the amount of capital (in units of $1000) invested.
Deriving partially concerning x and y in the production function we have:
Deriving partially concerning the variable x and concerning the variable y in the production function:
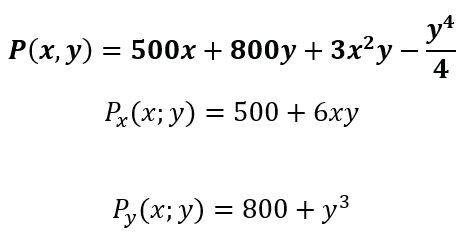
Substituting x=50 e y=20 en Px (x; y) y Py (x; y)
Interpretation of the results
In conclusion, when the size of the labor force equals 50 working hours per week and, the invested capital is kept fixed at 20 ($1000 units) the computer output increases by 6500 units produced.
Similarly, when the capital invested is 20 ($1000 units) and the labor force size is held fixed at 50 labor hours per week the output of computers increases to 8800 units produced.
3.The cost (in dollars) of a small furniture company to manufacture a unit of various items other than wood is given by:
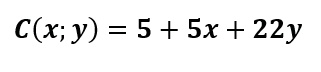
where x represents the number of board feet used and y expresses the number of working hours needed for assembly and finishing. If it takes 20 board feet and 2.5 labor hours to make a bookcase, find the manufacturing cost.
Solution:
Let x be the number of board feet used.
Let y be the number of working hours required for assembly and finishing.
To solve this situation we only need to substitute x=20 e and y =2.5 in the original function.
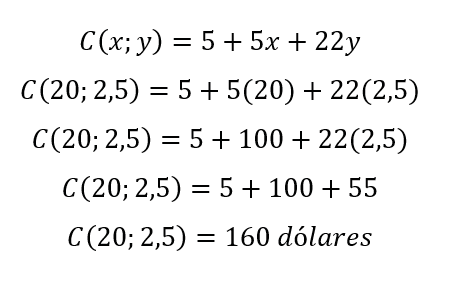
Answer: The manufacturing cost of a bookcase will be $160.
4.Assume that the output of Q units of a company’s product is determined by the Cobb-Douglas production function
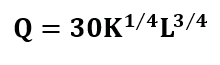
Where K represents the capital investment in dollars and L the labor hours.
a.Find Q if K= $10 000 and L=625 hours.
Replacing we have:

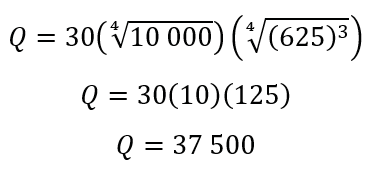
Answer: When the capital invested is $10 000 and 625 hours are worked, the units produced will be 37 500.
b.What happens if the investment and the hours worked are halved? Then K=$5 000 and L=312.5 hours.
Replacing we have:
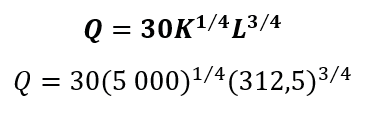
Converting the powers to roots yields the following:
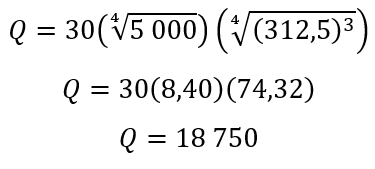
Answer: When capital invested and hours worked are halved output is also halved.
c.If capital investment is kept at $ 10,000, plot the graph of Q as a function of L.
The equation would be:
Figure 2.
Plot of Q as a function of L.
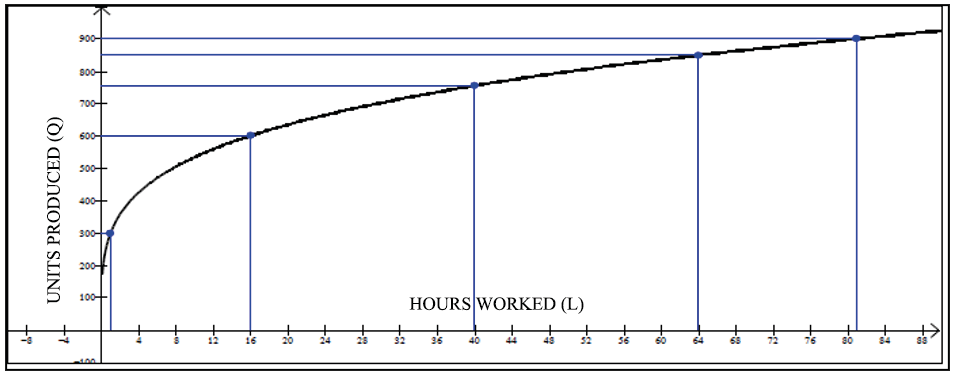
Own creation
5.A bakery produces white chocolates and dark chocolate. The material and labor cost of producing a kilogram of white chocolate is $6 and dark $5. Assume that the company has weekly fixed costs of $1200.
a.Find the weekly cost as a function of the number of kilograms of chocolates of each type produced per week.
b.Assume that the bakery sells a kilogram of white chocolate for $10 and dark chocolate for $8. Obtain the monthly utility function as a function of the number of kilograms of each type produced and sold per week.
Solution:
a.The material and labor costs of producing q1 kilograms of white chocolate and q2 kilograms of dark chocolate are given by 6q1 and 5q2 respectively.
The joint cost in this case is given by
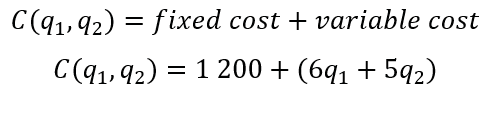
b.First, we will obtain the joint revenue function, it is clear that

Finally, we have that
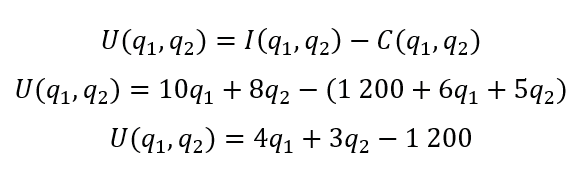
6.The production function of a firm is where P is the output obtained when I units of labor and k units of capital are employed. If at a given time 243 units of labor and 32 units of capital are employed.
a.Approximate the effect on output of increasing labor to 248 units and decreasing capital to 31 monetary units.
b.Calculate the percentage change in output.
Solution:
a.If we represent the change in output as dt, and the increase in labor and capital as dl and dk, respectively we will have the equation.
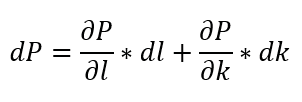
The partial derivatives are:
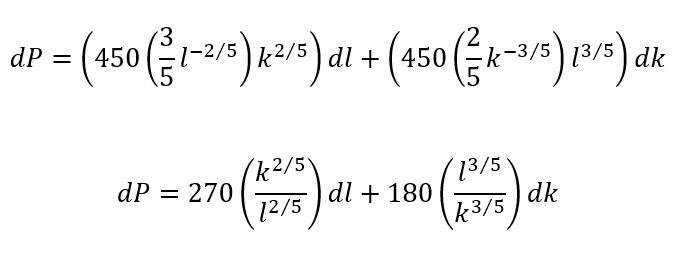
If we have that l = 243, k = 32, then:
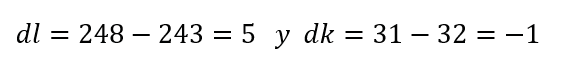
Substituting the values in
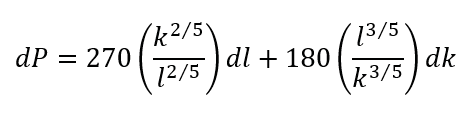
We have
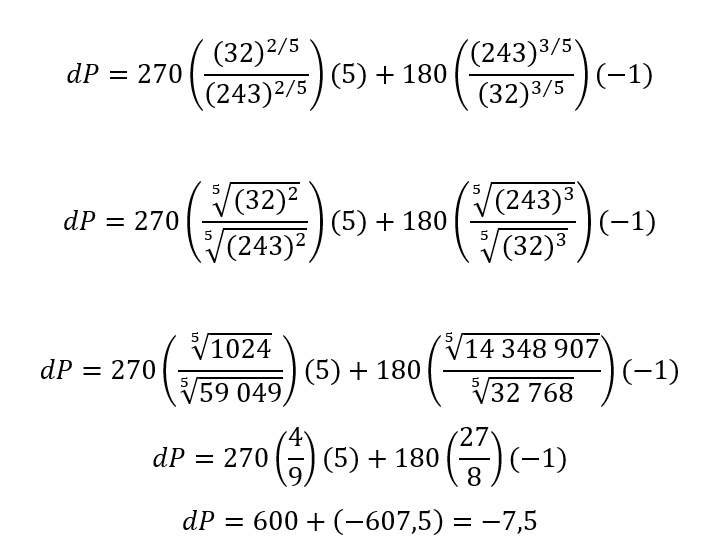
Answer: Thus, production decreases by approximately 7.5 units.
b.The percentage change in production is

Answer: Production falls by 0.015%.
4. CONCLUSIONS
Theoretical and practical aspects of the different applications of partial derivatives in economic sciences based on problem-solving were reviewed.
Taking into account the theoretical foundations, a brief historical review of mathematics about the economic sciences was made, highlighting the importance and its applicability in this area of knowledge.
In addition, the general aspects of partial derivatives such as definition, notation, and the different types that exist as a basic foundation for problem solving were taken into account.
The different applications of partial derivatives and their relation with the economic sciences were analyzed in a general way, taking into account different bibliographies from which solved and mostly proposed situations were taken.
A series of problems are proposed with their respective detailed solutions and analysis of the answers, including cost and production problems.
WORKS CITED
Brousseau, G. (1983). Fondements et méthodes de la didactique des mathématiques. Recherches en Didactique des Mathématiques, 7(2).
Cando, J. A. (2020). Determinación de los costos de producción de la empresa "PELILEO STORE". Ecuador: SENESCYT.
Hernández Mendoza , S. L., y Duana Avila , D. (2020). Técnicas e instrumentos de recolección de datos . Boletín Científico de las Ciencias Económico Administreativas del ICEA, 9(17), 51-53. https://repository.uaeh.edu.mx/revistas/index.php/icea/issue/archive
Hernández Sampieri, R., Fernández Collado, C., y Baptista Lucio, M. d. (2014). Metodología de la investigación. México.D.F: McGraw-Hill Interamericana.
Herrera Castrillo, C. J. (2023). Interdisciplinariedad a través de la Investigación en Matemática y Física. Revista Chilena de Educación Matemática, 15(1), 31-45. doi:https://doi.org/10.46219/rechiem.v15i1.126
Moriana, M. B. (2003). ECONOMÍA Y MATEMÁTICAS; PRODUCTIVIDAD, TRABAJO Y DISTRIBUCIÓN DE. Madrid-España.
Taylor, S. J., y Bogdan, R. (2001). Introducción a los métodos cualitativos de investigación (3 ed.). Paidós Ibérica, S.A.
Valhondo, J. B., y Llovera Sáez, F. J. (2014). Organización de la producción: una perspectiva histórica. Barcelona-España: ESERP.