ISSN 2410-5708 / e-ISSN 2313-7215
Año 13 | No. 38 | Octubre 2024 - Enero 2025
© Copyright (2024). Universidad Nacional Autónoma de Nicaragua, Managua.
Este documento está bajo una licencia Creative Commons
internacional
Reconocimiento-NoComercial-SinDerivados 4.0.
Integrales dobles en el cálculo de la densidad de circulación de fluidos en un campo vectorial
https://doi.org/10.5377/rtu.v13i38.19126
Enviado el 13 de enero, 2023 / Aceptado el 7 de junio, 2024
Jonny Ever Rodríguez Díaz
Profesor de Educación Media con Mención en Física-Matemática
Elmer Misael Rivera González
Profesor de Educación Media con Mención en Física-Matemática.
Universidad Nacional Autónoma de Nicaragua, Managua.
Facultad Regional Multidisciplinaria de Estelí
Freddy Josué Altamirano Vásquez
Profesor de Educación Media con Mención en Física-Matemática.
Universidad Nacional Autónoma de Nicaragua, Managua.
Facultad Regional Multidisciplinaria de Estelí.
Cliffor Jerry Herrera Castrillo
Máster en Matemática Aplicada.
Universidad Nacional Autónoma de Nicaragua, Managua. Facultad Regional Multidisciplinaria de Estelí.
Universidad Nacional Autónoma de Nicaragua, Managua.
Facultad Regional Multidisciplinaria de Estelí.
Sección: Educación
ARTÍCULOS CIENTÍFICOS
Palabras Clave: Integrales dobles, densidad, fluido, caudal volumétrico, campo vectorial, evaluación educativa.
Resumen
El presente artículo tiene como objetivo analizar las aplicaciones de integrales dobles en el cálculo de la densidad de circulación de fluidos en un campo vectorial. Se aplicó el enfoque cualitativo, así mismo, se utilizó el diseño documental por ser un estudio descriptivo, en el cual se analizan conceptos básicos de integrales, campos vectoriales, fluidos, volumen de sólidos, caudal volumétrico, propiedades y tipos de evaluaciones educativas que forman parte de la columna vertebral de este trabajo. La recolección de datos fue mediante la observación de videos en la plataforma de YouTube, entrevistas a maestros universitarios, libros de textos y artículos de revista relacionados con el tema de integrales dobles, campos vectoriales y fluidos. Así mismo, para el análisis de la información fue necesario la triangulación de teorías, tomando en cuenta los diferentes puntos de vista de los investigadores con respecto al tema con el fin de llegar a una conclusión y darle solución a los dos problemas inéditos planteados a través del análisis de diferentes variables físicas y matemáticas, los cuales están relacionados con la interdisciplinariedad de cálculo integral, cálculo vectorial y mecánica de fluido. Para el análisis de resultados fue necesario la resolución de dos problemas para poner en práctica todo lo analizado y descrito en el referente teórico y dar así cumplimiento a los objetivos del trabajo.
Abstract
The objective of this article is to analyze the applications of double integrals in the calculation of fluid flow density in a vector field. The qualitative approach was applied, likewise, the documentary design was used because it is a descriptive study, in which basic concepts of integrals, vector fields, fluids, volume of solids, volumetric flow, properties and types of educational evaluations that are part of the backbone of this work are analyzed. Data collection was through the observation of videos on the YouTube platform, interviews with university teachers, textbooks and journal articles related to the topic of double integrals, vector fields and fluids. Likewise, for the analysis of the information it was necessary the triangulation of theories, taking into account the different points of view of the researchers regarding the topic in order to reach a conclusion and give a solution to the two unpublished problems posed through the analysis of different physical and mathematical variables, which are related to the interdisciplinary nature of integral calculus, vector calculus and fluid mechanics. For the analysis of the results it was necessary to solve two problems in order to put into practice everything analyzed and described in the theoretical reference and thus fulfill the objectives of the work.
1. INTRODUCCIÓN
La presente investigación se ha llevado a cabo para facilitar información sobre el tema, integrales dobles en el cálculo de la densidad de circulación de fluido en un campo vectorial y proponer problemas aplicando los conceptos y fórmulas indicadas para darle salida al tema y sus objetivos, el cual será de gran utilidad para estudiantes universitarios y docentes interesados en la materia. Este contenido es de gran complejidad para comprenderlo, ya que no se encuentran documentos o libros que hablen de manera clara y sencilla; por eso se ha dado a la tarea de realizar un análisis científico para la correcta comprensión de la temática.
Se ha propuesto describir conceptos y propiedades fundamentales de la interdisciplinariedad: Cálculo, Álgebra, Estructura de la Materia y Evaluación Educativa, que formarán los componentes teóricos que fueron de utilidad para analizar y aplicarlos en la resolución de problemas mediante el análisis de tales aplicaciones. De esa manera se iniciará la explicación para abordar el tema, una vez entendido todo lo teórico se puede llevar a la práctica, a través de la solución de problemas que involucran varias asignaturas.
Según Rogawski, (2012) define las integrales dobles como:
La integral doble de f sobre D se define como la integral de f sobre R:
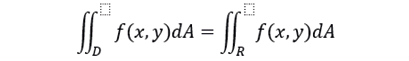
se dice que f es integrable sobre D si la integral de f sobre R existe. El valor de la integral no depende de la elección concreta de R pues f es cero fuera de D. (p. 878)
La búsqueda de información y redacción de este documento se hace porque analizar, describir y aplicar conceptos, propiedades y algunos principios sobre la integral doble en el cálculo de la densidad de circulación de un fluido en un campo vectorial, resulta complejo por ser un tema con muchas oportunidades y retos en el que se necesita, realizar un análisis científico de las variables en juego y llevarlo a la práctica, mediante la resolución de problemas, además, no hay un documento o libro que hable de manera clara y sencilla, es por eso que este trabajo será un gran aporte a la comunidad científica y educativa sirviendo a aquellos estudiantes universitarios y docentes que necesiten conocer y enriquecer sus conocimientos sobre el tema analizado y así utilizarlos en diferentes campos de estudio y la docencia de manera precisa y confiable.
Los aportes de docentes universitarios, libros de cálculo integral y proyectos de investigación relacionados con este tema antes descrito, da seguridad, factibilidad y credibilidad de ser auténticamente útil y confiable. Además, cabe mencionar que este estudio básicamente se enfoca en la solución de problemas de cálculo de densidad de circulación de fluido en campos vectoriales al utilizar integrales dobles.
La importancia de esta investigación de carácter científico consiste en enriquecer los conocimientos de todos aquellos interesados en conocer más acerca de fluidos en circulación, sus características, campos vectoriales y propiedades fundamentales de integración que son útil para ser aplicados en problemas relacionados con la vida cotidiana, por ejemplo: cálculo de la densidad de un determinado fluido que es útil para darse cuenta de que tipo de fluido es debido a su densidad o para saber si un determinado objeto puede flotar en ese líquido a su densidad. El trabajo realizado servirá como punto de partida para otras investigaciones o como complemento de conocimientos.
El principal beneficio es que el lector clarifique sus posibles dudas e inquietudes y obtenga los conocimientos necesarios y los reproduzca para beneficio de la comunidad educativa. Con certeza este documento será de gran utilidad y provecho, ya que contiene información clara y concisa que es muy utilizada en la Ingeniería Civil, Ingeniería Eléctrica y Estructura de la Materia, por mencionar algunas, así como la resolución de problemas relacionados con volúmenes de sólidos, cálculo de densidad, entre otros.
2. MÉTODOS
2.1. Tipo de Estudio
En la presente investigación se trabajó bajo un enfoque cualitativo, ya que este depende que la información que se tenga una preparación, organización de datos confiables y de calidad para aprender con mayor facilidad el análisis del contenido, mostrando la realidad en su contexto natural, el cual es dar solución a problemas. Según Bejarano, (2016) considera que: “el método cualitativo asume la inducción como vía para el desarrollo de criterios que permitan determinar la validez de los diferentes conocimientos” (p. 2).
En el presente trabajo se llevó a cabo una investigación cualitativa. Como define Álvarez (2011) “este es un diseño flexible a partir de información cualitativa, que no implica un manejo estadístico riguroso, ya que su estructura se orienta más al proceso que a la obtención de resultados” (p. 109). Así mismo, se utilizó el diseño documental siendo este un estudio descriptivo, el cual intenta obtener, analizar, interpretar y comparar información sobre el tema de estudio; el cual tiene como propósito ampliar y profundizar el conocimiento desde su naturaleza principal.
Paradigma: según León, (2016), define paradigma como: “acciones que se llevan a cabo de cierta forma establecida para obtener conclusiones individuales o en conjunto. Funciona así, porque de alguna manera representa creencias y costumbres que llevan a actuar de cierta manera, aunque no representa una verdad absoluta” (p. 1).
2.2. Recolección de la Información
La recolección de datos es mediante la observación de videos en la plataforma de YouTube, conversaciones a maestros universitarios que imparten cálculo integral, además, análisis de diversos libros de textos en digital de autores muy reconocidos como: Tom Apóstol, James Stewart y Louis Leithold, por mencionar algunos, además, artículos de revista anteriormente elaborados por universidades internacionales de España y México relacionados al tema de integral doble en el cálculo de la densidad de circulación de fluidos en un campo vectorial.
2.3. Análisis de la Información
Para el análisis de la información fue necesario la “triangulación de teorías” para así tomar en cuenta los diferentes puntos de vista de los investigadores con respecto al tema con el fin de llegar a una conclusión concreta. Los autores Benavides y Gómez-Restrepo, (2005) agregan que: “en este tipo de triangulación se establecen distintas teorías para observar un fenómeno con el fin de producir un entendimiento de como diferentes suposiciones afectan los hallazgo e interpretaciones de un mismo grupo de datos o información” (p. 123).
3. ANÁLISIS Y DISCUSIÓN DE RESULTADOS
La resolución de dos problemas inéditos propuestos a continuación, están basados en función de darle salida a cada uno de los objetivos planteados por el equipo investigador en el presente trabajo. Se pretende dar por confirmado que si se puede o no resolver problemas de densidad de circulación de fluidos a través de la aplicación de integrales dobles. Con la recopilación de la información y la descripción de los diferentes conceptos, fórmulas de integrales dobles, campos vectoriales y fluidos que se encuentran plasmados en el referente teórico, es necesario realizar la aplicación de estos puntos en la resolución de problemas inéditos relacionados con la vida cotidiana para constatar así la importancia, la eficiencia y eficacia del estudio realizado.
Los siguientes problemas se basan en la interdisciplinariedad haciendo uso de las integrales dobles para calcular el volumen de un sólido. Un tubo por donde circula un fluido, el cual representa un campo vectorial debido a la circulación del mismo con una determinada velocidad de desplazamiento y cálculo de la densidad del tanque que contiene el fluido (agua), dándole así solución a la temática planteada de este trabajo de investigación.
A continuación, la siguiente representación gráfica de la estructura de un tanque en forma de un paraboloide elíptico, el cual está siendo llenado por un líquido (agua) que circula por una tubería: en la vida cotidiana de los seres humanos se ve a diario cuando se pone a llenar una pila, tanques o cualquier otro envase, y surgió la incógnita de la velocidad de él agua, cuánto tiempo tardará un envase en llenarse, etc.
• Resolución del problema propuesto número 1
Un tanque en forma de paraboloide elíptico tiene ecuación x2+y2 =z y se encuentra dentro de un cilindro que tiene como ecuación x2+y2=3 , si este es llenado por un fluido(agua) en 50 minutos a través de una tubería de 10 cm de diámetro, determinar:
Volumen (v) del tanque en (m3 )
Caudal (Q) del agua en la tubería en m3/s
Velocidad del agua de la tubería en (m/s)
Densidad (p) del agua contenida en el tanque en kg/m 3
Figura 1
Representación gráfica del tanque de agua
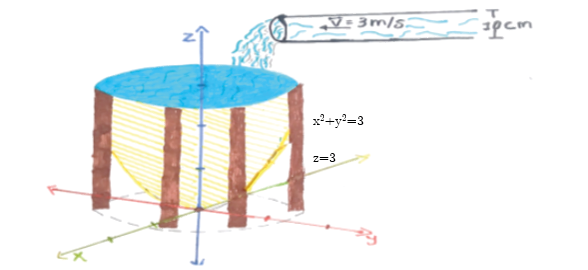
Creación Propia
Figura 2
Simulación del tanque de agua en el plano tridimensional
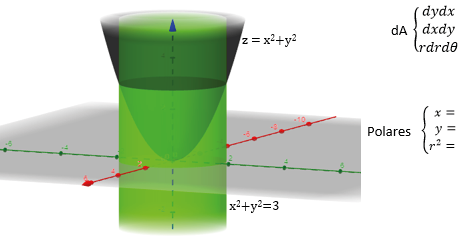
Creación Propia
Siendo x2+y2=3 la ecuación del cilindro con base inferior sobre el eje XY y base superior en el borde del tanque se obtiene el radio del mismo transformando la ecuación cartesiana a ecuación polar:
Si, x2+y2=3 ecuación cartesiana y
x2+y2=r2 , ecuación polar
Entonces, x2+y2 = x2+y2 , y
r2=3 , por tanto
r=√3, esto corresponde al radio de la base del cilindro que se encuentra sobre el eje xy
Figura 3
Proyección de la base del cilindro en el plano xy
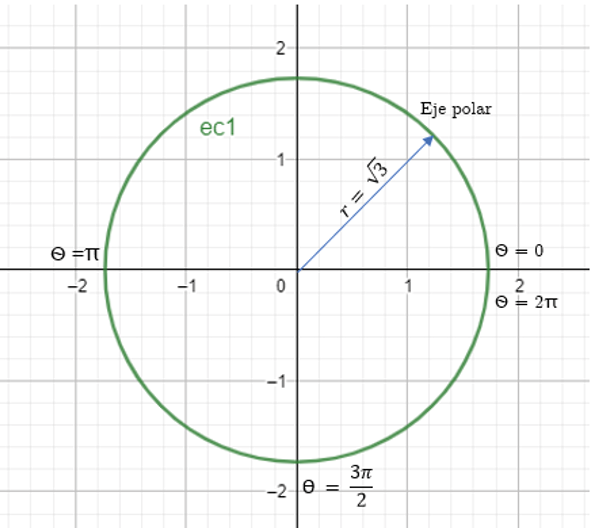
Creación Propia
Paso 1.
Cálculo del volumen que está entre el paraboloide y el cilindro:
Antes de resolver las integrales dobles para el cálculo del volumen de un sólido es necesario conocer las variables necesarias para su desarrollo las cuales son: los límites de integración, una función y el diferencial de área en coordenadas polares.
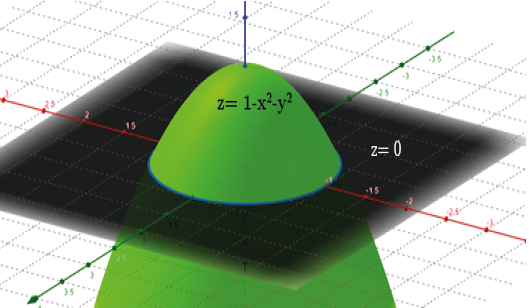
1. Cálculo de los límites de integración utilizando coordenadas polares, tomando en cuenta que el diferencial de área es: Da = rdrdθ, apoyados con la figura número (7).
Límite de integración para dr: Dimensión del Radio 0 ≤ r ≤ √3
Límite de integración para dθ: Ángulo barrido por el eje polar 0 ≤ θ ≤2π
2. Al convertir la ecuación del paraboloide elíptico z = x2+y2 a una función con respecto a la variable z quedaría:
Si z=f(x,y), entonces f (x,y) = x2+y2
3. dA= rdrdθ
Sustituir los datos en la integral doble para volumen:
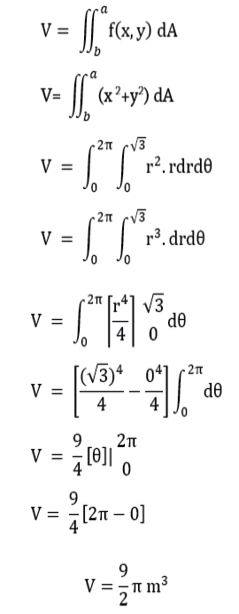
Paso 2.
• El volumen del cilindro con ecuación x2+y2=3 y su base inferior sobre el plano XY es:
Si x2+y2=3 y z = x2+y2 , entonces z = 3 , esto corresponde a la altura del cilindro.
h= 3 y r= √3
Volumen del cilindro (V=πr2 h)
V= π(√3m)2 (3m) = π(3m2) (3m) = 9m3
Paso 3.
El volumen del cilindro menos el volumen de la sección atrapada entre el cilindro y el paraboloide es igual al volumen del tanque, es decir:
Volumen del tanque es:
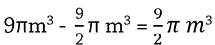
Paso 4.
• Cálculo del caudal volumétrico de la tubería y velocidad del agua:
Tabla 1
Cálculo del caudal volumétrico y velocidad de circulación del fluido en la tubería
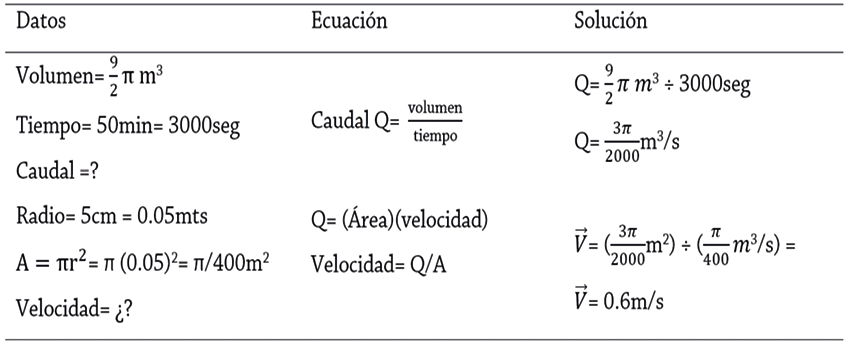
Creación Propia
Paso 5.
•Cálculo de la masa del agua contenida en el tanque:
Si un metro cúbico contiene 1000 litros de agua, entonces, son:
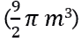
(1000 litros) = 14137.67 litros
Tomando en cuenta que un litro de agua equivale a 1 kg de masa, entonces, el agua del tanque contiene una masa de 14137.67 kilogramos.
Paso 6.
•Cálculo de la densidad del tanque de agua:
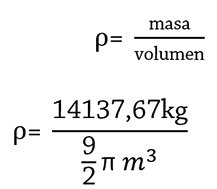
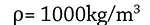
“Por tanto, la densidad del agua contenida en el tanque es de 1000 kg/m3”
•Resolución del problema propuesto número 2
A continuación, la siguiente representación gráfica de la estructura de un recipiente en forma de un paraboloide elíptico que abre hacia abajo, el cual está lleno por un fluido (aceite vegetal), el objetivo es calcular su densidad, el volumen y en cuanto tiempo se vaciaría si se le hace un agujero de 4 centímetros de diámetros
Figura 4
Representación del recipiente en el plano tridimensional
Creación Propia
Paso 1
“Encontrar el radio de la circunferencia formado entre la intersección del paraboloide y el plano xy”
Siendo z= 1-x2-y2 la ecuación del recipiente y z= 0 la del plano que corta el paraboloide en el plano xy, es necesario igualar las ecuaciones para encontrar el radio de dicha región de intersección
Si, z= 1-x2-y2 , y
z= 0, entonces,
0 = 1-x2-y2 (despejar x e y)
-x2-y2= -1 (multiplicar toda la expresión por -1)
x2+y2= 1 (convertir la ecuación cartesiana a ecuación polar para encontrar el radio tomando en cuenta las equivalencias polares de la parte derecha)
Si x2+y2 = 1 y x2+y2= r2, entonces:
R2= 1 (despejando r)
R= 1 (radio de la base del paraboloide sobre el plano xy)

Pasó 2
Encontrar los límites de integración para calcular el volumen del recipiente por medio de las integrales dobles para volúmenes
Figura 5
Proyección del corte del paraboloide sobre el plano xy
Creación Propia
Cálculo de los límites de integración utilizando coordenadas polares, tomando en cuenta que el diferencial de área es: Da = rdrdθ, apoyados con la figura número (15).
Límite de integración para dr: Dimensión del Radio 0 ≤ r ≤ 1
Límite de integración para dθ: Ángulo barrido por el eje polar 0 ≤θ ≤2π
Pasó 3
“Convertir las formula del paraboloide elíptico a una función f(x,y) con respecto a z para aplicarla en la fórmula de la integral”
Al convertir la ecuación del paraboloide elíptico z = 1-x2-y2 a una función con respecto a la variable z quedaría:
Si z=f(x,y), entonces:
f (x,y) = 1-x2-y2 (Convertir la función a polar)
f(r,θ) = 1- (r cos θ)2 – (r sin θ)2 (Resolver las potencias)
f(r,θ) = 1- r2 cos2 θ – r2 sin2 θ (Sacando r2 como factor común)
f(r,θ) = 1- r2(cos2 θ + r2 sin2 θ) (Aplicando la identidad pitagórica, cos2θ + sin2θ = 1)
f(r,θ) = 1- r2
•Resolver las integrales dobles para volumen
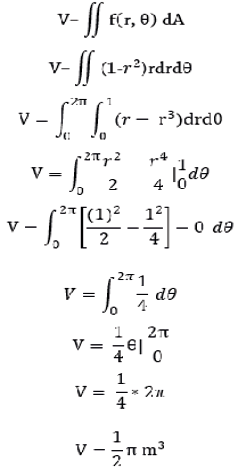
“Por tanto, el volumen del recipiente es
 , aproximadamente 1. 57 metros cúbicos de aceite vegetal”
, aproximadamente 1. 57 metros cúbicos de aceite vegetal”
Pasó 4
“Cálculo de la densidad del aceite”

Pasó 5
“Cálculo del tiempo que tardaría el recipiente en vaciarse si se le sale el aceite por un orificio de 4 centímetros de radio a una velocidad de 2 m/s.”
Tabla 1
Cálculo del caudal volumétrico y el tiempo de vaciado del recipiente

Creación Propia
Los dos problemas inéditos resueltos en las páginas anteriores se refieren a fluidos contenidos en recipientes grandes en forma de paraboloides elípticos, de estos era necesario calcular su densidad, pero para ello antes fue necesario calcular otras variantes (área del tubo por donde salía el fluido, volumen del tanque, caudal volumétrico y la masa del líquido). Estas variantes se calculan con ecuaciones que se encuentran en el referente teórico y otras fórmulas que son muy utilizadas comúnmente como: (volumen del cilindro y área del círculo) seguidamente se llegó a la conclusión del problema calculando la densidad y así dar solución al objetivo dos (aplicar conceptos y fórmulas en problemas inéditos).
IV. CONCLUSIONES
Los conceptos y fórmulas descritas son de calidad y sobre todo de fuentes confiables y que pueden ser utilizadas por los lectores para fortalecer su conocimiento. Además, han sido de gran utilidad al grupo investigador para resolver problemas matemáticos.
Aplicar los conceptos, fórmulas de integrales y propiedades de fluidos, apoyados con un buen análisis matemático, ayudan a resolver problemas relacionados al cálculo de la densidad de circulación de un fluido en un campo vectorial. Además, el uso de herramientas tecnológicas (GeoGebra 3D), son claves para tener una mejor perspectiva de las diferentes gráficas tridimensionales y así poder hacer un buen análisis del problema que se pretenda resolver aplicando también todo lo teórico incluido en este documento.
El contenido de este documento acerca de integrales dobles es para ser aplicado a estudiantes universitarios, debido al nivel de complejidad que presenta. Por otra parte, se finaliza que los objetivos planificados se cumplieron a cabalidad debido a la solución correcta de los problemas inéditos propuestos.
La evaluación es fundamental para determinar la calidad de los conceptos teóricos desarrollados, por tanto, se presentan aplicaciones de estos conceptos para así obtener una excelente consolidación de los aprendizajes en los estudiantes o la sociedad en general que se han tomado el reto de conocer más acerca del tema plasmado en este trabajo de investigación. “El secreto del éxito está en la persistencia de los individuos y en el amor al conocimiento”.
GLOSARIO DE TÉRMINOS TÉCNICOS O ESPECIALIZADOS
|
Significado |
||
|
h |
Altura |
|
|
Q |
Caudal volumétrico |
|
|
cosθ |
coseno de theta |
|
|
ρ |
Densidad |
|
|
Da |
Diferencial de área |
|
|
rdrdθ |
Diferencial de área en coordenadas polares |
|
|
dθ |
Diferencial del ángulo |
|
|
dr |
Diferencial del radio |
|
|
f |
Función |
|
|
kg |
Kilogramos |
|
|
≥ |
Mayor o igual que |
|
|
le |
Menor o igual que |
|
|
m3 |
Metros cúbicos |
|
|
N |
Newton |
|
|
(x,y) |
Par ordenado x, y |
|
|
r |
Radio |
|
|
sinθ |
Seno de theta |
|
|
tanθ |
Tangente de theta |
|
|
T |
Tiempo |
|
|
Velocidad |
|
|
V |
Volumen |
|
REFERENCIAS
Álvarez, C. A. (2011). Metodología de la investigación cuantitativa y cualitativa. https://www.uv.mx/rmipe/files/2017/02/Guia-didactica-metodologia-de-la-investigacion.pdf
Bejarano, M. A. (2016). La investigacion cualitativa. INNOVA Research Journal. https://scholar.google.es/scholar?hl=es&assdt=%2C5&q=estudio+
cualitativo+concepto&oq=#d=gs_qads&t=16
64510263735&u=%23p%3DsHfujMSalJQJ
Benavides, M. O., & Gómez Restrepo, C. (2005). Metodos en investigacion cualitativa: triangulación. Revista Colombiana de Psiquiatría, 123. https://scholar.google.es/scholar?/hl=es&as_sdt=0%2C5&q=triangulacion+
de+teorias&oq=#d=gs_qads&t=1664513429
974&u=%23p%3DCWzTJnm8qQUJ
León, R. d. (2016). Tipos de paradigmas. Cursos online web: https;//cursosonlineweb.com/paradigmas.html
Rogawski, J. (2012). Cálculo de varias variables segunda edición. Barcelona, España : Editorial Reverte, S. A. https://es.scribd.com/document/501849039/calculo-de-varias-variables-Rogawski