ISSN 2410-5708 / e-ISSN 2313-7215
Year 13 | No. 38 | October 2024- January 2025
© Copyright (2024). National Autonomous University of Nicaragua, Managua.
This document is under a Creative Commons
Attribution-NonCommercial-NoDerivs 4.0 International licence.
Double integrals in the calculation of fluid flow density in a vector field
https://doi.org/10.5377/rtu.v13i38.19126
Submitted on january 13th, 2023 / Accepted on june 7th, 2024
Jonny Ever Rodríguez Díaz
Secondary Education Teacher with a Minor in Physics-Mathematics.
National Autonomous University of Nicaragua, Managua.
Multidisciplinary Regional Faculty of Estelí.
Elmer Misael Rivera González
Secondary Education Teacher with a Minor in Physics-Mathematics.
National Autonomous University of Nicaragua, Managua.
Multidisciplinary Regional Faculty of Estelí.
Freddy Josué Altamirano Vásquez
Secondary Education Teacher with a Minor in Physics-Mathematics.
National Autonomous University of Nicaragua, Managua.
Multidisciplinary Regional Faculty of Estelí.
Clifford Jerry Herrera Castrillo
Secondary Education Teacher with a Minor in Physics-Mathematics.
National Autonomous University of Nicaragua, Managua.
Multidisciplinary Regional Faculty of Estelí.
Section: Education
Scientific research article
Keywords: Double integrals, Density, Fluid, Volumetric flow, Vector field, Educational assessment
ABSTRACT
The objective of this article is to analyze the applications of double integrals in the calculation of fluid circulation density in a vector field. The qualitative approach was applied, likewise, the documentary design was used because it is a descriptive study, in which basic concepts of integrals, vector fields, fluids, volume of solids, volumetric flow, properties, and types of educational evaluations that are part of the backbone of this work are analyzed. Data collection was through the observation of videos on the YouTube platform, interviews with university teachers, textbooks, and journal articles related to the topic of double integrals, vector fields, and fluids. Likewise, for the analysis of the information, it was necessary to triangulate theories, taking into account the different points of view of the researchers regarding the subject to reach a conclusion and provide solutions to the two unprecedented problems posed through the analysis of different physical and mathematical variables. which are related to the interdisciplinarity of integral calculus, vector calculus, and fluid mechanics. For the analysis of results, it was necessary to solve two problems to put into practice everything analyzed and described in the theoretical reference and thus comply with the objectives of the work.
INTRODUCTION
The present research has been carried out to provide information on the subject, double integrals in the calculation of the fluid circulation density in a vector field and to propose problems applying the concepts and formulas indicated to give an outlet to the topic and its objectives, which will be very useful for university students and teachers interested in the subject. This content is very complex to understand since there are no documents or books that speak clearly and simply; that is why it has been given the task of carrying out a scientific analysis for the correct understanding of the subject.
It has been proposed to describe fundamental concepts and properties of interdisciplinarity: Calculus, Algebra, Structure of Matter, and Educational Evaluation, which will form the theoretical components that were useful to analyze and apply them in the resolution of problems through the analysis of such applications. In this way, the explanation will begin to address the topic, once all the theoretical is understood, it can be put into practice, through the solution of problems that involve several subjects.
According to Rogawski, (2012) defines double integrals as:
The double integral of the envelope is defined as the integral of the fDf envelope: R
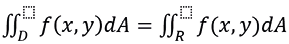
it is said to be integrable on whether the integral of the envelope exists. The value of the integral does not depend on the concrete choice of R since f is zero outside D. (p. 878)
The search for information and writing of this document is done because analyzing, describing, and applying concepts, properties, and some principles about the double integral in the calculation of the circulation density of a fluid in a vector field, is complex because it is a subject with many opportunities and challenges in which it is needed, carry out a scientific analysis of the variables at play and put it into practice, through problem-solving, in addition, there is no document or book that speaks clearly and simply, that is why this work will be a great contribution to the scientific and educational community serving those university students and teachers who need to know and enrich their knowledge on the subject analyzed and thus use them in different fields of study and teaching accurately and reliably.
The contributions of university professors, comprehensive calculus books, and research projects related to this topic described above, give security, feasibility, and credibility of being authentically useful and reliable. In addition, it is worth mentioning that this study focuses on the solution of fluid circulation density calculation problems in vector fields by using double integrals.
The importance of this scientific research is to enrich the knowledge of all those interested in knowing more about circulating fluids, their characteristics, vector fields, and fundamental integration properties that are useful to be applied in problems related to everyday life, for example: calculation of the density of a certain fluid that is useful to realize what type of fluid it is due to its density or to to know if a certain object can float in that liquid at its density. The work carried out will serve as a starting point for other research or as a complement to knowledge.
The main benefit is that the reader clarifies their possible doubts and concerns obtains the necessary knowledge and reproduces it for the benefit of the educational community. This document will certainly be very useful and useful, since it contains clear and concise information that is widely used in Civil Engineering, Electrical Engineering, and Structure of Matter, to mention a few, as well as the resolution of problems related to solid volumes, density calculation, among others.
1. METHODS
1.1. Type of Study
In this research, we worked under a qualitative approach, since this depends on the information that has a preparation, and organization of reliable and quality data to learn more easily the analysis of the content, showing reality in its natural context, which is to provide solutions to problems. According to Bejarano, (2016) considers that: "the qualitative method assumes induction as a way to develop criteria that allow determining the validity of different knowledge" (p. 2).
In the present work, qualitative research was carried out. As Álvarez (2011) defines "this is a flexible design based on qualitative information, which does not imply rigorous statistical management, since its structure is oriented more to the process than to obtaining results" (p. 109). Likewise, the documentary design was used, this being a descriptive study, which tries to obtain, analyze, interpret, and compare information on the subject of study; which aims to broaden and deepen knowledge from its main nature.
Paradigm: León (2016), defines paradigm as: "actions that are carried out in a certain established way to obtain individual or joint conclusions. It works like this because in some way it represents beliefs and customs that lead to acting in a certain way, although it does not represent an absolute truth" (p. 1).
1.2. Collection of Information
The data collection is through the observation of videos on the YouTube platform, conversations with university professors who teach integral calculus, in addition, analysis of various digital textbooks by well-known authors such as Tom Apóstol, James Stewart, and Louis Leithold, to mention a few, in addition, journal articles previously prepared by international universities in Spain and Mexico related to the topic of double integral in the calculation of the density of fluid circulation in a vector field.
1.3. Information Analysis
For the analysis of the information, it was necessary to "triangulate theories" to take into account the different points of view of the researchers regarding the subject to reach a concrete conclusion. The authors Benavides and Gómez-Restrepo (2005) add that: "in this type of triangulation, different theories are established to observe a phenomenon to produce an understanding of how different assumptions affect the findings and interpretations of the same group of data or information" (p. 123).
2. ANALYSIS AND DISCUSSION OF RESULTS
The resolution of two unpublished problems proposed below is based on the function of solving each of the objectives proposed by the research team in this work. It is intended to confirm whether or not fluid circulation density problems can be solved through the application of double integrals. With the compilation of information and the description of the different concepts, formulas of double integrals, vector fields, and fluids that are embodied in the theoretical reference, it is necessary to apply these points in the resolution of unprecedented problems related to everyday life in order to verify the importance, efficiency, and effectiveness of the study carried out.
The following problems are based on interdisciplinarity making use of double integrals to calculate the volume of a solid. A tube through which a fluid circulates, which represents a vector field due to its circulation with a certain speed of displacement and calculation of the density of the tank that contains the fluid (water), thus providing a solution to the theme raised by this research work.
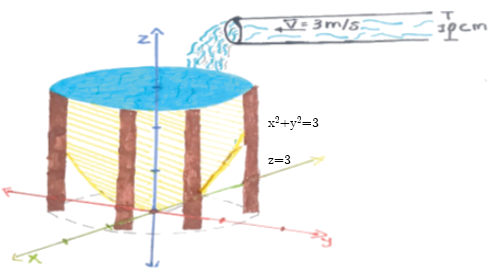
Below is the following graphic representation of the structure of a tank in the form of an elliptical paraboloid, which is being filled by a liquid (water) circulating through a pipe: in the daily life of human beings it is seen daily when a battery, tanks or any other container is filled. and the question arose of the speed of the water, how long it will take for a container to fill, etc.
• Solving Proposed Problem No. 1
An elliptical paraboloid-shaped tank has an equation and is inside a cylinder that has as an equation, if it is filled by a fluid (water) in 50 minutes through a pipe of 10 cm in diameter, x²+y² =zx²+y²=3 determine:
Tank volume () in ()vm³
Flow rate () of water in the pipe in Qm³/s
Pipeline Water Velocity in ()m/s
Density () of the water contained in the tank in
Figure 1
Graphical representation of the water tank
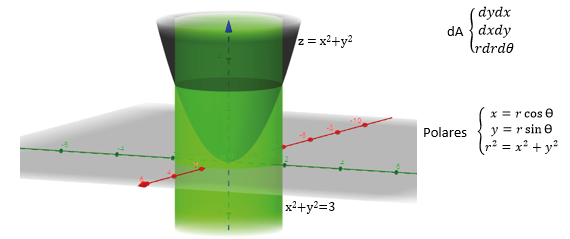
Own creation
Figure 2
Simulation of the water tank in the three-dimensional plane
Own creation
Being x²+y²=3 the equation of the cylinder with a lower base on the axis and an upper base on the edge of the tank, the XY radius of the same is obtained, transforming the Cartesian equation into a polar equation:
Yes, the Cartesian equation and x²+y2=3
x²+y²=r² , polar equation
So, x²+y² = , and x²+y²
r²=3 therefore
r=√3, this corresponds to the radius of the cylinder base that is on the shaft xy
Figure 3
Projection of the cylinder base on the plane xy
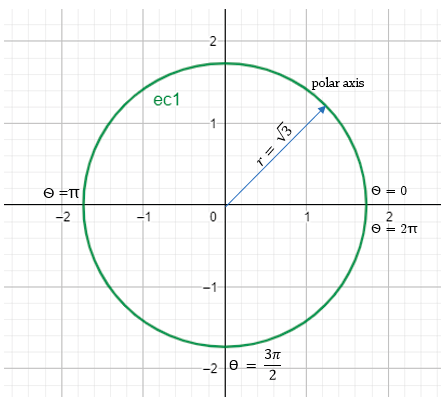
Own creation
Step 1.
Calculation of the volume between the paraboloid and the cylinder:
Before solving the double integrals for the calculation of the volume of a solid, it is necessary to know the variables necessary for its development, which are: the limits of integration, a function, and the differential of area in polar coordinates.
1. Calculation of the integration limits using polar coordinates, taking into account that the area differential is: Da = rdrd θ, supported by figure number (7).
Integration limit for Radius dimension dr0 ≤ r ≤ 3
Integration limit for : Angle swept by the polar axis 0 ≤ θ ≤2π
2. Converting the equation of the elliptic paraboloid to a function concerning the variable would be: z = x2+y² z
If , then z=f(x,y)f (x,y) = x²+y²
3. dA= rdrdθ
Replace the data in the double integral for volume:
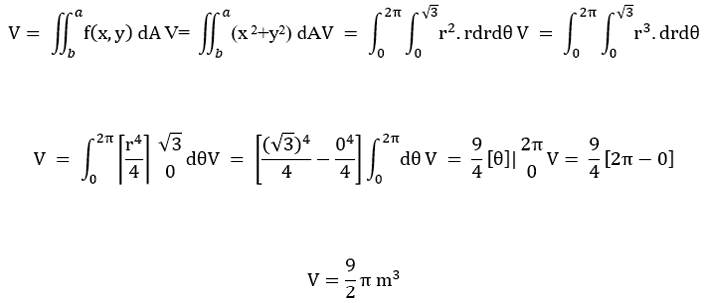
Step 2.
• The volume of the cylinder with the equation and its base lower on the plane is: x2+y2=3 XY
If and, then, this corresponds to the height of the cylinder. x²+y²=3z = x²+y²z = 3
h= 3 and r= √3
Cylinder Volume ()V=πr² h
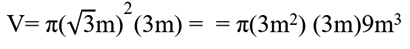
Step 3.
The volume of the cylinder minus the volume of the section trapped between the cylinder and the paraboloid is equal to the volume of the tank, i.e.:
Tank volume is: =
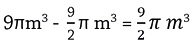
Step 4.
• Calculation of the volumetric flow of the pipe and water velocity:
Table 1
Calculation of the volumetric flow rate and circulation velocity of the fluid in the pipeline

Own creation
Step 5.
Calculation of the mass of the water contained in the tank:
If one cubic meter contains 1000 liters of water, then, are:
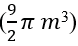
(1000 liters) = 14137.67 liters
Taking into account that one liter of water is equivalent to 1 kg of mass, then, the water in the tank contains a mass of 14137.67 kilograms.
Step 6.
• Water tank density calculation:

"Therefore, the density of the water contained in the tank is 1000 kg/m3"
• Solving Proposed Problem No. 2
Next, the following graphic representation of the structure of a container in the form of an elliptical paraboloid that opens downwards, which is filled with a fluid (vegetable oil), the objective is to calculate its density, volume, and how long it would take to empty it if a hole of 4 centimeters in diameter is made
Figure 4
Representation of the container in the three-dimensional plane
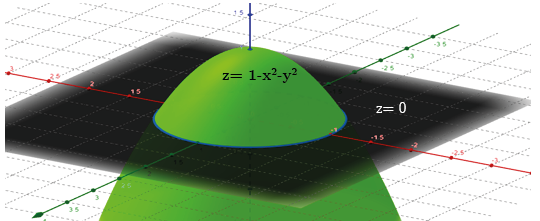
Own creation
Step 1
"Find the radius of the circumference formed between the intersection of the paraboloid and the plane xy"
Since z= 1-x²-y² the equation of the container and z= 0 is that of the plane that cuts the paraboloid in the plane, it is necessary to match the equations to find the radius of that region of intersection xy
Yes, z= 1-x²-y² , and
z= 0then
0 = 1-x2-y2 (clear x and y)
-x2-y2= -1 (multiply the entire expression by -1)
x2+y2= 1 (convert the Cartesian equation to the polar equation to find the radius taking into account the polar equivalences on the right side)
If x2+y2 = 1 and x2+y2= r2, then:
R2= 1 (Dumping r)
R= 1 (radius of the base of the paraboloid above the plane)xy
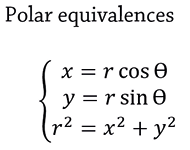
Passed 2
Find the integration limits to calculate the volume of the container using the double integrals for volumes
Figure 5
Projection of the paraboloid cut onto the plane xy
Own creation
Calculation of the integration limits using polar coordinates, taking into account that the area differential is:
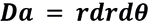 , supported by figure number (15).
, supported by figure number (15).
Integration limit for Radius dimension dr0 ≤ r ≤ 1
Integration limit for : Angle swept by the polar axis 0 ≤ θ ≤2π
Passed 3
"Convert the formula of the elliptical paraboloid to a function concerning to apply it in the formula of the integral"f(x,y) z
Converting the equation of the elliptic paraboloid to a function concerning the variable would be: z = 1-x²-y² z
If , then:z=f(x,y)
f (x,y) = 1-x²-y² (Convert the function to polar)
f(r,θ) = 1- (r cos θ)² – (r sin θ)² (Resolve the powers)
f (r,θ) = 1- r²cos²θ - r²sin²θ (Taking out r2 as a common factor)
f(r,θ) = 1- r²(cos²θ+ sin²θ) (Applying the Pythagorean identity, cos2θ+ sin2θ = 1)
f(r,θ) = 1- r²
-Solve double integrals for volume
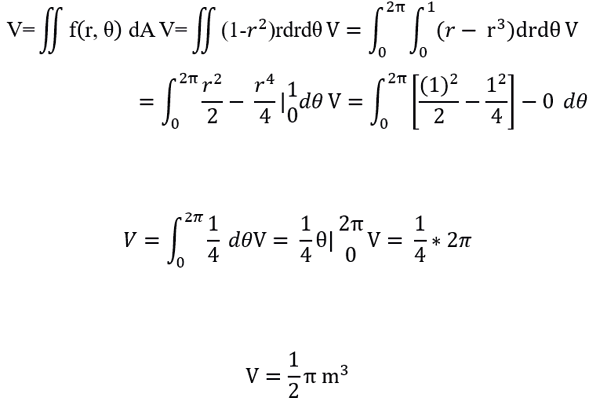
"Therefore, the volume of the container is
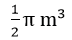 , approximately 1. 57 cubic meters of vegetable oil "
, approximately 1. 57 cubic meters of vegetable oil "
Passed 4
"Calculating the density of the oil"
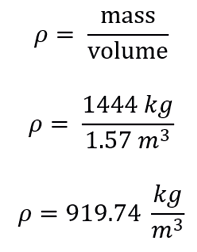
Passed 5
"Calculation of the time it would take for the container to empty if the oil leaks out of a hole with a radius of 4 centimeters at a speed of 2 m/s."
Table 1
Calculation of the volume flow rate and the emptying time of the container
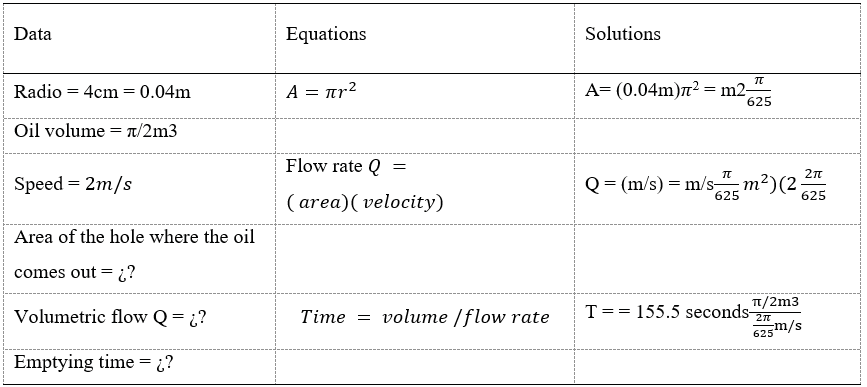
Own creation
The two unpublished problems solved in the previous pages refer to fluids contained in large containers in the form of elliptical paraboloids, of which it was necessary to calculate their density, but it was necessary to calculate other variants (area of the tube through which the fluid came out, volume of the tank, volumetric flow and the mass of the liquid). These variants are calculated with equations found in the theoretical reference and other formulas that are widely used such as: (cylinder volume and circle area) then the conclusion of the problem was reached by calculating the density and thus solving objective two (applying concepts and formulas in unpublished problems).
3. CONCLUSIONS
The concepts and formulas described are of quality and above all from reliable sources and can be used by readers to strengthen their knowledge. In addition, they have been very useful to the research group to solve mathematical problems.
Applying the concepts, formulas of integrals, and properties of fluids, supported by good mathematical analysis, helps to solve problems related to the calculation of the circulation density of a fluid in a vector field. In addition, the use of technological tools (GeoGebra 3D) is key to having a better perspective of the different three-dimensional graphs and thus being able to make a good analysis of the problem to be solved, also applying all the theories included in this document.
The content of this document about double integrals is to be applied to university students, due to the level of complexity it presents. On the other hand, it is concluded that the planned objectives were fully met due to the correct solution to the proposed unprecedented problems.
Evaluation is essential to determine the quality of the theoretical concepts developed, therefore, applications of these concepts are presented to obtain an excellent consolidation of learning in students or society in general who have taken the challenge of knowing more about the topic reflected in this research work. "The secret of success lies in the persistence of individuals and the love of knowledge."
work cited
Álvarez, C. A. (2011). Quantitative and qualitative research methodology. Retrieved from https://www.uv.mx/rmipe/files/2017/02/Guia-didactica-metodologia-de-la-investigacion.pdf
Bejarano, M. A. (2016). La investigacion cualitativa. INNOVA Research Journal. Obtenido de https://scholar.goo gle.es/scholar?hl=es&as_sdt=%2C5&q=estudio+cualitativo+conce pto&oq=#d=gs_qads&t=1664510263 735&u=%23p%3DsHfujMSalJQJ
Benavides, M. O., & Gómez Restrepo, C. (2005). Methods in qualitative research: triangulation. Colombian Journal of Psychiatry, 123. Retrieved from https://scholar.google.es/scholar?/hl=es&as_sdt=0%2C5&q=triangulacion+de+teo rias&oq=#d=gs_qads&t=1664513429 974&u=%23p%3DCWzTJnm8qQUJ
León, R. D. (2016). Types of paradigms. Retrieved from Online web courses: https;//cursosonlineweb.com/paradigmas.html
Rogawski, J. (2012). Calculation of several variables second edition. Barcelona, Spain : Editorial Reverte, S. A. Retrieved from https://es.scribd.com/document/501849039/calculo-de-varias-variables-Rogawski